判断矩形能否放入多边形内——cad c# 二次开发实现
效果如下:
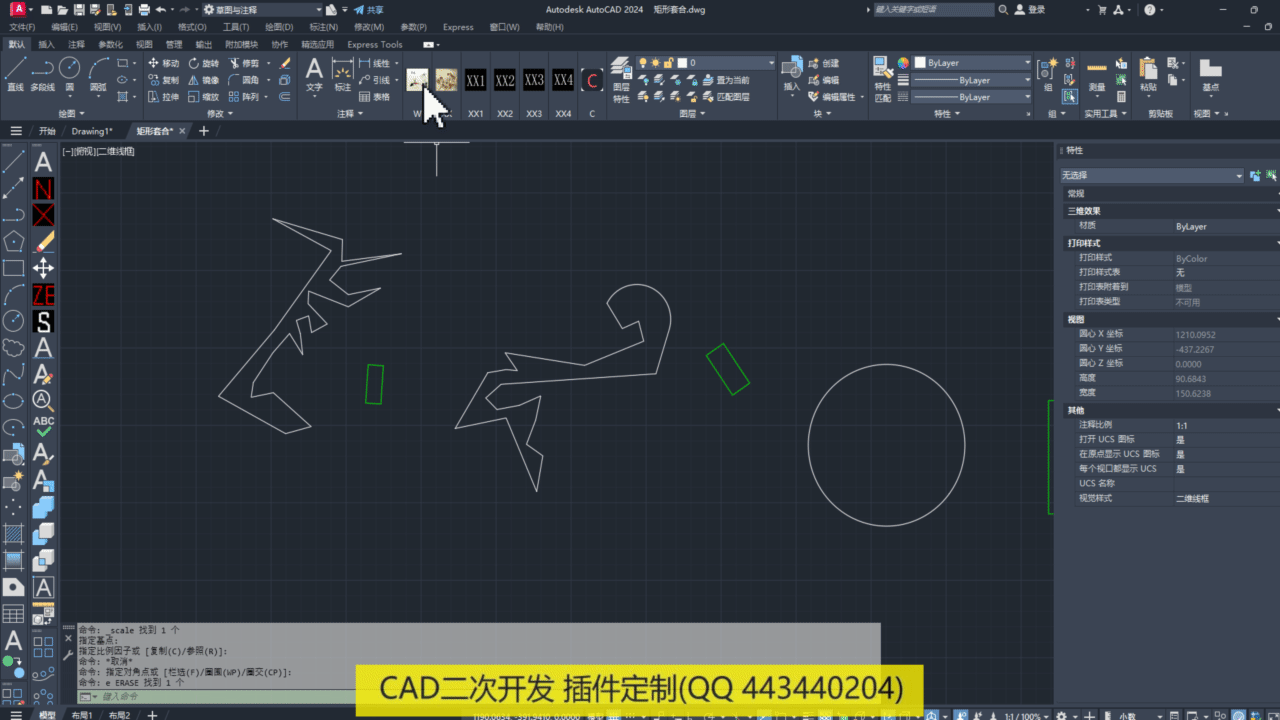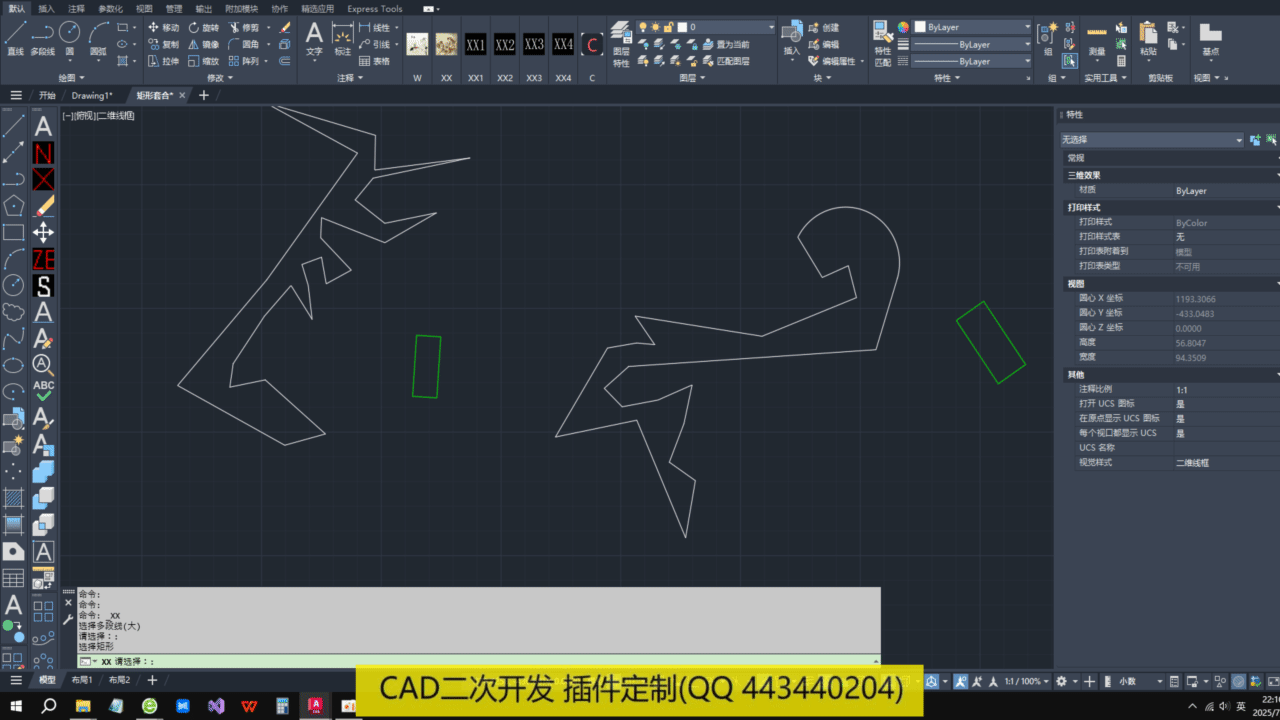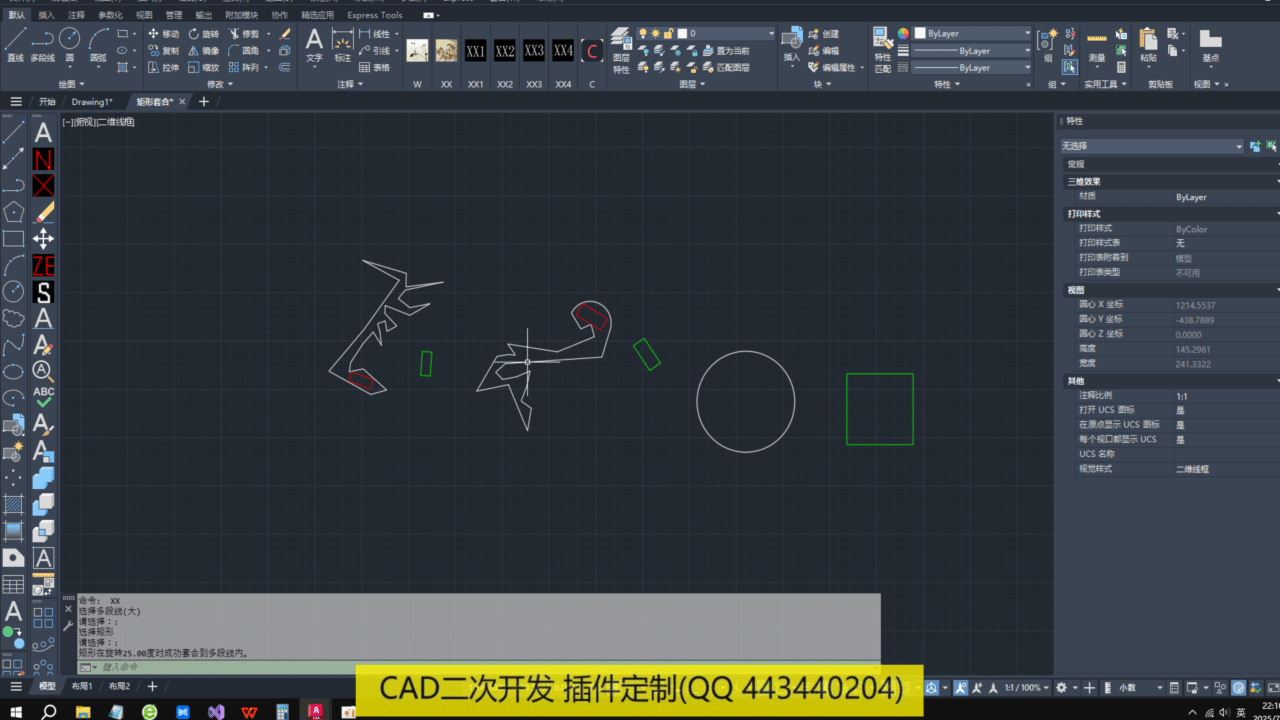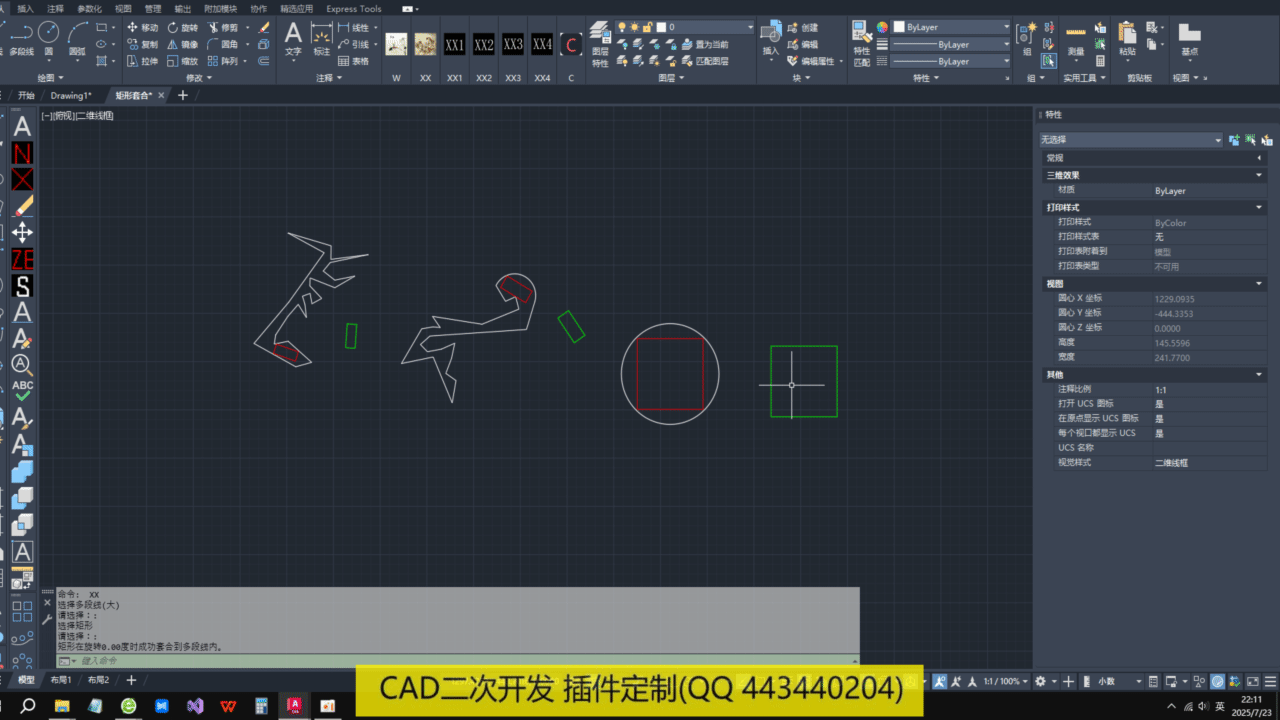
逻辑过程如下:对多段线内部布点阵,将矩形移动到点阵中旋转,直到跟多边形无交点为止。
主函数代码 如下:
public void 多段线容纳矩形(){int 点阵密度 = 50; // 点阵密度,多段线包围盒最小边长的倒数 可调整Document doc = Application.DocumentManager.MdiActiveDocument;Database db = doc.Database;Editor ed = doc.Editor;ed.WriteMessage("\n选择多段线(大)");var pl = db.SelectEntity2<Polyline>(true);if (pl is null) return;ed.WriteMessage("\n选择矩形");var rectOrigon = db.SelectEntity2<Polyline>(true);if (rectOrigon is null) return;//求出矩形的中心点坐标var zxd = rectOrigon.GeometricExtents.CenterPoint2();//指定点阵间距var space = Math.Min( pl.GeometricExtents.Height2(), pl.GeometricExtents.Width2()) / 点阵密度; // 取多段线的最大边长的1/20作为点阵间距//生成点阵var dianzhens = pl.GenerateInnerPoints(space);if (dianzhens == null || dianzhens.Count <= 0) { ed.WriteMessage("\n没有生成点阵"); return; }var dbpoints = new List<DBPoint>();foreach (var point in dianzhens){dbpoints.Add(point.toDBPoint2());}//画出点阵if (dbpoints.Count <= 0) return;//db.AddEntityToModeSpace(dbpoints.ToArray());//// 设置点样式为“正方形内有个圆”(PDMODE = 35)//Application.SetSystemVariable("PDMODE", 66);//97//// 设置点大小为1,相对单位(PDSIZE 为负值)//Application.SetSystemVariable("PDSIZE", -0.3);//遍历点阵foreach (var point in dianzhens){var(isok, resultjuxing) = 矩形绕点旋转( pl, rectOrigon, zxd, point,db, ed);if (isok) return;}ed.WriteMessage("\n没有找到合适的矩形位置。");}
