【金融机器学习】第四章：风险-收益权衡——Bryan Kelly, 修大成（中文翻译）

第四章：风险-收益权衡

前一章节主要讨论了不涉及风险-收益权衡的监督预测模型，因此不构成资产定价模型。本章将利用无监督与半监督学习方法，建立明确建模风险-收益权衡的因子定价模型。

4.1 套利定价理论（APT）基础

Ross（1976）提出的套利定价理论（APT）为数据驱动的因子定价模型机器学习分析奠定了基础。该理论表明，通过部分模型设定——本质上仅需线性因子结构、固定数量的因子以及无套利的最小经济假设——我们可以仅通过研究因子组合来学习资产定价模型，并理解收益中哪些成分是可分散的，哪些不可分散。换言之，APT为风险-收益权衡的实证分析提供了蓝图，而无需了解资产定价因子的形成机制。因此，潜在因子分析的机器学习方法可用于对实证资产定价现象进行全新且有力的分析。

Giglio等（2022a）对收益因子模型进行了综述，将文献分为因子可观测、贝塔可观测或两者均不可观测三类。可观测因子或贝塔催生了时间序列和横截面回归方法。本章重点关注因子与贝塔均为潜在（或至多部分可观测）的更复杂情况，从而深入探讨机器学习因子建模技术的细节。

4.2 无条件因子模型

Ross（1976）APT的前提是以下统计因子模型：

$$R_t=\alpha +\beta F_t+{ϵ}_t,\text{\hspace{1em}(4.1)}$$

其中$R_t$为$N\times 1$维个股超额收益向量，$\beta$为$N\times K$维因子载荷矩阵，$F_t$为$K\times 1$维潜在因子向量（其均值$\gamma =E(F_t)$可解释为因子风险溢价），${ϵ}_t$为$N\times 1$维零均值残差向量。

$N\times 1$维截距向量$\alpha$代表定价误差，即未被因子暴露解释的预期收益部分。Ross（1976）的APT及其后续研究（如Huberman, 1982; Ingersoll, 1984; Chamberlain和Rothschild, 1983）证明，近似无套利条件等价于${}^1$

$${\alpha }^{\prime }Var({ϵ}_t{)}^{-1}\alpha {\lesssim }_{\text{P}}1,\text{当}N\to \infty .\text{\hspace{1em}(4.2)}$$

即随着投资标的增加，承担 idiosyncratic 风险的补偿不会无限扩大。

${}^1$符号$a\underset{P}{\lesssim }b$表示$a=O_P(b)$，$a\underset{P}{\asymp }b$表示$a\underset{P}{\lesssim }b$且$b\underset{P}{\lesssim }a$。

4.2.1 主成分分析（PCA）估计因子

基于APT，Chamberlain和Rothschild（1983）与Connor和Korajczyk（1986, 1988）提出在因子与贝塔均潜在时采用PCA作为因子模型估计方法。更便捷的等价方法是对去均值收益矩阵$\bar{R}=R-(\frac{1}{T}{\sum }_{t=1}^T{R}_t){\nu }_T^{\prime }$进行奇异值分解（SVD）：

$$\bar{R}=\sum _{j=1}^{\hat{K}}{\sigma }_j{\xi }_j{\xi }_j^{\prime }+\hat{U},\text{\hspace{1em}(4.3)}$$

其中{σj}\{\sigma_j\}{σj​}、{ξj}\{\xi_j\}{ξj​}和{ξj}\{\xi_j\}{ξj​}分别为$\bar{R}$前$\hat{K}$个奇异值及左右奇异向量，$\hat{K}$为因子数量的相合估计量（如Bai和Ng, 2002），$\hat{U}$为残差矩阵，${\nu }_T$为$T\times 1$维单位向量。该分解可得到因子创新$V_t=F_t-E(F_t)$与风险暴露$\beta$的估计：

$$\hat{V}=T^{1/2}({\xi }_1,{\xi }_2,\dots ,{\xi }_{\hat{K}}),\hat{\beta }=T^{-1/2}({\sigma }_1{\zeta }_1,{\sigma }_2{\zeta }_2,\dots ,{\sigma }_{\hat{K}}{\zeta }_{\hat{K}}).\text{\hspace{1em}(4.4)}$$

因子估计经标准化满足$\hat{V}{\hat{V}}^{\prime }=T{\mathbb{I}}_{\hat{K}}$。亦可对$\hat{\beta }$标准化使$\hat{\beta }\hat{\beta }=N{\mathbb{I}}_{\hat{K}}$。潜在因子模型存在固有不可识别性——因子旋转与载荷反向旋转不会改变数据生成过程。因此，因子及其载荷仅可识别至可逆线性变换（即旋转）。Bai（2003）证明了PCA估计的相合性，并在所有因子均为 pervasive（即${\lambda }_K({\beta }^{\prime }\beta ){\approx }_{P}N$）的假设下推导了其渐近分布。

Connor和Korajczyk（1988）首次使用约1,500只股票的大横截面数据检验潜在因子模型性能，发现基于PCA的因子模型虽优于CAPM，但仍存在显著定价误差。总体而言，无条件因子模型难以描述个股数据。基于此，无条件潜在因子模型（及PCA估计）在Connor和Korajczyk（1988）后一度式微。Kelly等（2020b）在1962-2014年CRSP股票面板中验证了这一结论，表明PCA对个股风险溢价的描述极不可靠。

近期PCA在收益因子建模中复兴。主要原因是PCA虽不适用于个股面板，但在组合面板建模中表现优异。例如Kelly等（2020b）、Kozak等（2018）和Pulkthuanthong等（2019）证明，基于异象组合面板估计的因子模型能以经济意义上较小的定价误差解释这些组合。这些研究继承了Geweke和Zhou（1996）采用Gibbs抽样从组合数据提取潜在因子的早期工作。

潜在因子方法的潜在缺陷在于因子旋转不可识别性导致的经济解释困难。但当关注目标具有旋转不变性时，该方法具有优势。下文将举例说明。

4.2.2 风险溢价的三步估计法

因子风险溢价反映投资者因承担该因子风险所要求的均衡补偿。许多经济理论模型基于非交易因子（如消费、GDP增长、通胀、流动性、气候风险等）。为估计非交易因子的风险溢价，需构建因子模拟组合并估计其预期收益。设该非交易因子$G_t$与资产横截面存在如下关系：

$$G_t=\xi +\eta V_t+Z_t,\text{\hspace{1em}(4.5)}$$

其中$Z_t$为测量误差，$V_t=F_t-\mathrm{E}(F_t)$。该模型中$G_t$的风险溢价为$\eta \gamma$。由于$G_t$可能源自经济理论，其模拟组合与风险溢价具有经济可解释性。且$\eta V_t$与$\eta \gamma$具有旋转不变性，尽管$V_t$、$\eta$和$\gamma$本身仅可识别至旋转。根据Bai和Ng（2002），存在矩阵$H$使得${\hat{V}}_t\stackrel{P}{\to }H{V}_t$。若将$R_t$和$G_t$的数据生成过程改写为$H{V}_t$的函数，则$V_t$的风险溢价变为$H\gamma$，$G_t$在$H{V}_t$上的载荷变为$\eta H^{-1}$，但模拟组合创新与$G_t$的风险溢价仍保持为$\eta H^{-1}H{V}_t=\eta V_t$和$\eta H^{-1}H\gamma =\eta \gamma$。

Giglio和Xiu（2021）提出结合Fama-MacBeth回归与PCA的三步估计法推断$\eta \gamma$。第一步通过(4.4)进行PCA估计因子与载荷；第二步通过Fama-MacBeth回归估计潜在因子风险溢价：

$$\hat{\gamma }=\frac{1}{T}\sum _{t=1}^T({\hat{\beta }}^{\prime }\hat{\beta }{)}^{-1}{\hat{\beta }}^{\prime }{R}_t.\text{\hspace{1em}(4.6)}$$

第三步估计$G_t$在潜在因子上的载荷：

$$\hat{\eta }=\frac{1}{T}\sum _{t=1}^T{G}_t{\hat{V}}_t^{\prime }.$$

风险溢价估计量即为$\hat{\eta }\gamma$。

Giglio和Xiu（2021）建立了该估计量的渐近性质。其对PCA输出的Fama-MacBeth回归渐近分析为潜在因子模型中的风险溢价、随机贴现因子（Giglio等, 2021b）和alpha（Giglio等, 2021a）等统计推断奠定了基础。

三步估计法与基于PCA回归的模拟组合构建密切相关。该过程等价于将$G_t$对$R_t$的主成分回归构建因子模拟组合，并通过计算其平均收益得到$G_t$的风险溢价。使用主成分而非原始资产是一种正则化方法。这一视角鼓励在构建模拟组合时采用机器学习中的其他正则化方法（如岭回归与Lasso）。

因子	无控制变量的两步回归	无控制变量的两步回归	包含FF3的两步回归	包含FF3的两步回归	三步回归	三步回归
流动性	2.26***	(0.90)	0.57	(0.68)	0.37**	(0.16)
中介资本	1.01***	(0.45)	0.43	(0.45)	0.60***	(0.31)
纽约气温	-319.01	(25.73)	-277.96**	(124.08)	-0.69	(13.90)
全球气温	-6.65	(4.85)	-3.33	(2.07)	0.05	(0.21)
厄尔尼诺	56.85***	(17.42)	-15.34**	(7.11)	0.41	(0.82)
太阳黑子	-409.37	(937.73)	882.89**	(405.40)	4.01	(35.63)
IP增长	-0.36***	(0.14)	-0.14**	(0.05)	-0.01*	(0.00)
宏观PC1	84.90***	(24.76)	39.96***	(13.57)	3.26**	(1.58)
宏观PC2	9.35	(15.93)	23.91***	(8.97)	-0.88	(1.27)
宏观PC3	-5.94	(14.30)	-31.24***	(9.74)	-1.25	(1.51)
消费增长	0.26*	(0.16)	0.07	(0.05)	0.00	(0.01)

表4.1：三步回归法的实证结果

说明：本表报告了不同方法下各因子的月化风险溢价估计（百分比），限制零贝塔率等于观测到的国债利率：两种版本的两步横截面回归（分别无控制因子和使用Fama-French三因子模型）；使用7个潜在因子的三步估计量。测试资产为647个按不同特征排序的组合（数据源自Giglio和Xiu, 2021的表B1）。

实证方面，表4.1比较了不同方法对多个非交易因子风险溢价的估计结果，包括工业生产增长（IP）的AR(1)创新、Ludvigson和Ng（2010）279个宏观金融变量前三个主成分的VAR(1)创新、Pástor和Stambaugh（2003）的流动性因子、He等（2017）的中介资本因子、Novy-Marx（2014）的四个因子（曼哈顿高温、全球地表温度异常、太平洋准周期温度异常"厄尔尼诺"、太阳黑子数量）以及Malloy等（2009）的总体消费因子。

该表揭示传统两步回归的两个问题：遗漏变量偏差与测量误差偏差。两步估计量依赖于研究者选择的控制因子，但经济理论常未明确应控制哪些因子。遗漏控制因子通常会导致风险溢价估计偏差。以流动性和中介资本因子为例，前者的风险溢价估计从单变量两步回归的226个基点/月降至加入FF3因子后的57个基点；后者从101个基点降至43个基点。

方程(4.5)也包含$\eta =0$的噪声因子与弱$\eta$小因子作为特例，这通常会扭曲两步回归中的风险溢价推断（Kan和Zhang, 1999首次记载）。例如Novy-Marx（2014）的四个因子在标准预测回归中看似能预测收益，但其与股市的经济联系较弱。然而基于FF3因子的两步回归中，其中三个因子显示显著风险溢价。宏观因子（如主成分或消费增长）也较弱。三步方法通过第一阶段估计潜在因子作为控制变量，第二阶段横截面回归消除遗漏变量偏差，第三阶段时间序列回归消除测量误差，从而解决这两个问题。表4.1最后两列的估计结果因此更具经济合理性。

4.2.3 PCA扩展

虽然PCA是最常用的因子提取方法，但存在具有独特特征的替代方法。例如Giglio等（2021a）采用矩阵补全法估计因子模型，可处理非平衡收益面板。设$\Omega$为$N\times T$矩阵，当$R_{i,t}$非缺失时$(i,t)$元素为1。矩阵补全算法求解以下凸优化问题：

$$\hat{X}=\arg \underset{X}{\min }\Vert (R-X)\circ \Omega {\Vert }^2+\lambda \Vert X{\Vert }_n,$$

其中$\circ$表示Hadamard积，∥X∥n=∑i=1min⁡{N,T}ψi(X)\|X\|_{n}=\sum_{i=1}^{\min\{N,T\}}\psi_{i}(X)∥X∥n​=∑i=1min{N,T}​ψi​(X)（${\psi }_i(X)$为$X$第$i$大奇异值），$\lambda$为调节参数。通过对$X$奇异值的${\ell }_1$范数惩罚，该算法尝试仅利用$R$的观测条目找到其低秩近似矩阵$\hat{X}$，进而通过SVD恢复潜在因子与载荷。

标准PCA对去均值超额收益矩阵$\bar{R}$应用SVD，仅利用收益的样本中心二阶矩估计潜在因子与贝塔。Lettau和Pelger（2020a）指出，PCA仅依赖二阶矩信息导致因子模型估计效率低下。资产定价理论通过无条件欧拉方程(1.2)版本在资产均值与因子贝塔间建立联系。因此他们认为，更充分利用收益数据一阶矩中的因子载荷信息可提升PCA估计量整体性能。基于此，他们开发了"风险溢价PCA"（RP-PCA）估计量，对收益的非中心二阶矩$T^{-1}{\sum }_{t=1}^T{R}_t{R}_t^{\prime }+\lambda (T^{-1}{\sum }_{t=1}^T{R}_t)(T^{-1}{\sum }_{t=1}^T{R}_t^{\prime })$应用PCA，其中$\lambda >-1$为调节参数。Connor和Korajczyk（1988）也使用非中心PCA，但仅限于$\lambda =0$情形，而标准PCA对应$\lambda =-1$。

Lettau和Peiger（2020a）建立了RP-PCA的渐近理论，证明在无定价误差且因子 pervasive 时其效率优于PCA。虽然标准PCA对定价误差存在具有稳健性，但定价误差项可能导致RP-PCA估计量有偏，因为预期收益不再与因子载荷平行。我们推测，若施加近似无套利的经济约束(4.2)，则$\alpha$的幅度渐近足够小，不会导致因子及其载荷估计的渐近偏差。${}^2$

Giglio等（2021b）指出因子强度取决于测试资产的选择。即使所有测试资产均为对该因子零暴露的多空组合，市场因子也可能变弱。为解决风险溢价估计中的弱因子问题，他们提出基于监督PCA（见3.5.2节）的测试资产选择流程。该方法还可用于检测随机贴现因子模型中的缺失因子。

${}^2$Bryzgalova等（2023）提出了其他基于经济动机的目标来识别潜在定价因子。

4.2.4 选择哪些因子？

解释股票横截面预期收益的因子搜索已产生数百个候选因子。其中许多是冗余的——给定其他因子后对资产定价无增量解释力；部分则完全无用——根本不具备解释力。

机器学习方法可通过降维与变量选择应对冗余与无用因子的挑战。例如，将平均收益对因子协方差进行Lasso回归，可识别出能够定价资产横截面的简约因子集。但同时，选择错误不可避免：过拟合可能导致选择无用变量；解释力较弱的变量可能被遗漏；冗余变量可能被误选。Feng等（2020）的图4.1显示，Lasso选择的变量在不同交叉验证随机种子间差异显著（参见图3.1）。

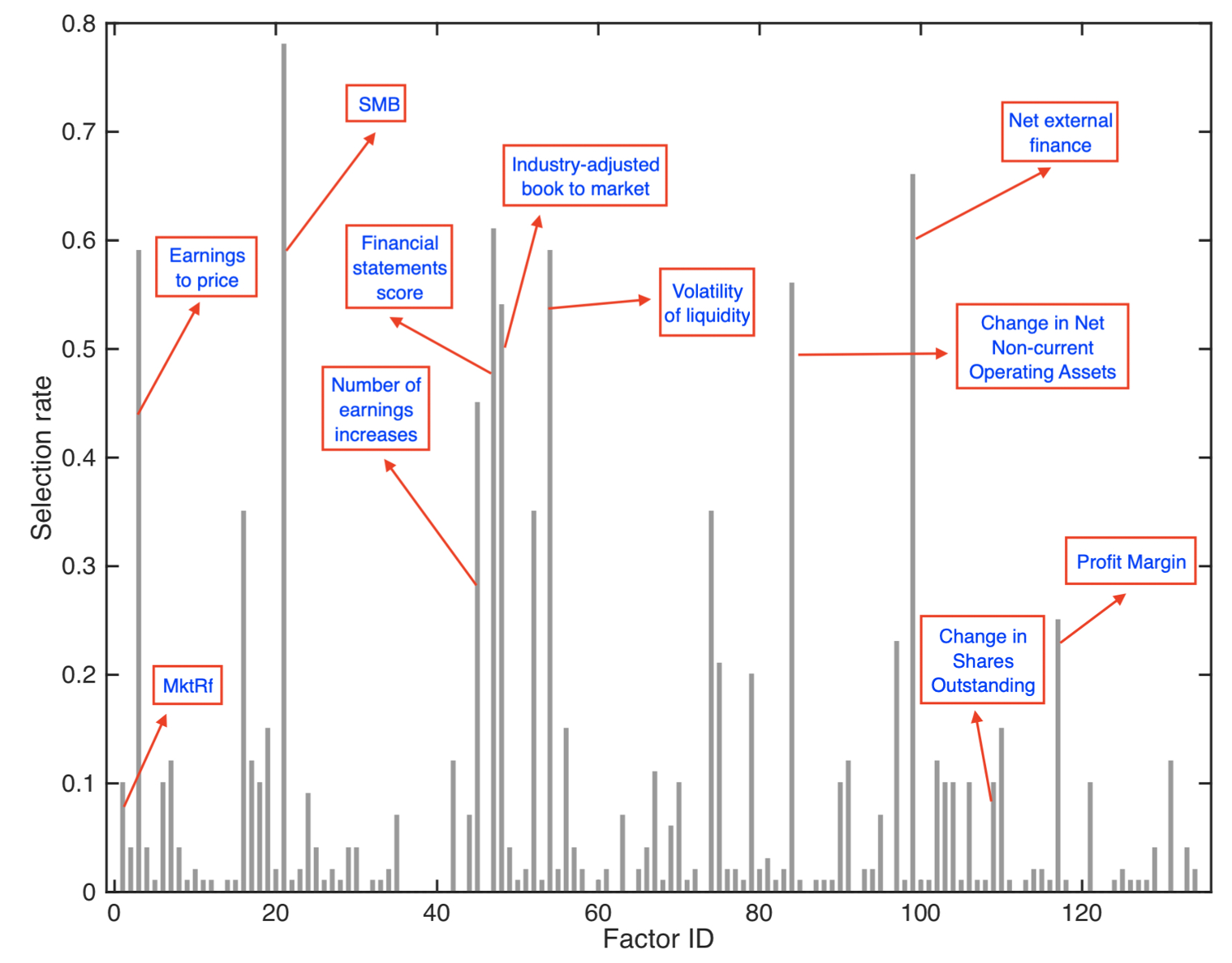
图4.1：因子选择频率

说明：来源：Feng等（2020）。横轴为因子ID，纵轴为200次随机交叉验证中Lasso回归选择各因子的频率。

Feng等（2020）提出将Chernozhukov等（2018）的双重机器学习框架与两步横截面回归结合的方法，识别一致的因子集，并推导其估计量的渐近分布，从而对因子进行统计推断。

实证中，Feng等（2020）将其推断程序递归应用于文献中陆续提出的120多个候选因子，区分有用因子与无用/冗余因子。结果显示，若自1994年起逐年应用该方法，仅有17个因子会被认为有用，绝大多数被判定为冗余或无用。

另一些文献从模型不确定性与模型平均视角研究因子模型选择，如Avramov等（2021）和Chib等（2023）。Avramov等（2021）表明，关于夏普比率上限的先验观点会影响因子与预测变量的纳入。总体而言，贝叶斯模型不确定性是金融机器学习中值得深入探讨的话题。

4.3 条件因子模型

前文主要讨论基于静态贝塔与风险价格的欧拉方程(1.2)无条件版本（通过将${\mathcal{I}}_t$替换为空集或"条件向下"推导）。通常，当改变条件集时，因子表示也会变化，因为资产的条件矩发生变化。仅当"条件向下"时资产贝塔与预期收益不变的特殊情况下，条件与无条件模型才相同。然而实证研究表明，资产协方差在时间序列上高度可预测，且大量证据表明资产均值也具有可预测性。换言之，我们可以排除"条件静态"这一特殊情况。

是否引入条件信息？这是构建收益因子模型时的关键问题。我们认为，只要可能，研究者应致力于建立有效的条件模型。条件模型更具野心——它们描述资产价格的状态依赖性，从而更精细地捕捉市场行为。但条件模型要求也更高，需要研究者提供总结当前状态的相关数据。此类条件信息可能范围广泛，且需要更丰富的参数化模型来捕捉细微的条件行为。当相关条件信息不可得时，无条件模型使研究者无需理解复杂的市场动态即可把握资产基本行为，且模型可能更简单。因此，早期收益因子分析文献多采用无条件设定（如前节所述）。本节我们聚焦条件模型设定。

类比(4.1)，向量化的条件潜在因子模型为：

$$R_{t+1}={\alpha }_t+{\beta }_t{F}_{t+1}+{ϵ}_{t+1},\text{\hspace{1em}(4.7)}$$

其中因子载荷与定价误差 now vary with the conditioning information set ${\mathcal{I}}_t$.

4.3.1 工具化主成分分析（IPCA）

若无额外限制，(4.7)右侧自由度过多，模型不可识别。Kelly等（2020b）的工具化主成分分析（IPCA）通过引入连接资产贝塔（及alpha）与可观测变量的限制取得进展。IPCA模型形式为：

$$R_{t+1}=\underset{{\alpha }_t}{\underbrace{Z_t{\Gamma }_{\alpha }}}+\underset{{\beta }_t}{\underbrace{Z_t{\Gamma }_{\beta }}}{F}_{t+1}+{ϵ}_{t+1},\text{\hspace{1em}(4.8)}$$

其中$Z_t$为$N\times L$维矩阵，包含每只资产$L$个可观测特征（或"工具变量"）数据。${}^3$ $F_{t+1}$仍为$K\times 1$维潜在因子向量。Harvey和Ferson（1999）及最近的Gagliardini等（2016）也将因子载荷建模为可观测变量的时变函数，但其因子完全可观测。

${}^3$通常$Z$中包含常数项。

IPCA模型的核心在于${\beta }_t$的设定。首先，时变工具变量直接将动态引入条件因子载荷。更根本地，引入工具变量允许额外数据塑造因子模型，不同于PCA等无条件潜在因子技术仅从收益数据估计因子结构。通过将载荷锚定于可观测数据，模型用数据部分替代不可识别参数，从而实现识别。

$L\times K$矩阵${\Gamma }_{\beta }$定义了从大量特征（$L$）到少量风险因子暴露（$K$）的映射。估计${\Gamma }_{\beta }$时，我们寻找能最佳描述潜在因子载荷结构的少数特征线性组合。考虑${\Gamma }_{\beta }$为$L$维单位矩阵的特例，此时$F_t$由与$R_{t+1}{Z}_t$成比例的$L$个潜在因子构成，特征决定这些因子上的贝塔。这让人联想到Rosenberg（1974）和MSCI Barra（业界常用因子风险模型）。Barra模型在$Z_t$中包含数十个特征与行业指标。当企业特征数量$L$较大时，自由参数数量等于因子实现{Ft}\{F_t\}{Ft​}的数量（即$L\times T$），通常相对于样本量过大。Barra因子存在显著冗余（少数主成分可解释其大部分联合变异），表明其可能过度参数化且低效。

IPCA通过特征空间降维解决该问题。若众多特征提供关于股票风险暴露的噪声但信息丰富的信号，则将特征聚合成线性组合可分离信号并平均噪声。

资产迁移（如股票从小盘成长演变为大盘价值）给使用时序方法建模个股条件预期收益带来挑战。标准解法是构建具有随时间相对稳定平均特征值的组合，但若需多个特征准确描述资产属性，该方法将不切实际。IPCA解决方案通过决定股票风险收益的特征参数化贝塔。IPCA通过贝塔（由资产特征定义）跟踪资产属性的迁移，从而无需研究者手动将资产分组为组合，因为模型明确通过特征跟踪资产属性。因此，该模型适应高维资产系统（如个股），无需临时性组合构建。

最后，(4.7)中的IPCA设定还允许特征可能代表alpha而非贝塔。传统资产定价模型假设资产间预期收益差异仅源于风险暴露差异。但当$L\times 1$维系数向量${\Gamma }_{\alpha }$非零时，股票特征可以不符合风险-收益权衡的方式预测收益。IPCA通过将alpha估计为特征线性组合（由${\Gamma }_{\alpha }$决定）来解决此问题，在控制特征在因子风险暴露中作用的同时最佳解释条件预期收益。若特征与股票平均收益的关系不同于其与风险因子载荷的关系，IPCA将估计非零${\Gamma }_{\alpha }$，从而识别错误定价（即与资产系统性风险暴露无关的持有补偿）。

测试资产	统计量	$K=1$	$K=3$	$K=4$	$K=5$	$K=6$
面板A：IPCA
个股	总$R^2$	14.9	17.6	18.2	18.7	19
	预测$R^2$	0.36	0.43	0.43	0.70	0.70
	$N_p$	636	1908	2544	3180	3816
组合	总$R^2$	90.3	97.1	98.0	98.4	98.8
	预测$R^2$	2.01	2.10	2.13	2.41	2.39
	$N_p$	636	1908	2544	3180	3816
面板B：可观测因子
个股	总$R^2$	11.9	18.9	20.9	21.9	23.7
	预测$R^2$	0.31	0.29	0.28	0.29	0.23
	$N_p$	11452	34356	45808	57260	68712
组合	总$R^2$	65.6	85.1	87.5	86.4	88.6
	预测$R^2$	1.67	2.07	1.98	2.06	1.96
	$N_p$	37	111	148	185	222

表4.2：IPCA与其他因子模型比较

说明：本表报告了受限（${\Gamma }_{\alpha }=0$）IPCA模型（面板A）与静态载荷可观测因子模型（面板B）的总$R^2$、预测$R^2$（百分比）及估计参数数量（$N_p$）。可观测因子模型设定为$K=1,3,4,5,6$时分别对应CAPM、FF3、FFC4、FF5和FFC6模型（数据源自Kelly等, 2020b的表2）。

表4.2比较了不同潜在因子数量的IPCA（面板A）与文献中其他领先模型。第一组比较模型包括采用传统逐资产时序回归方法估计的预设可观测因子。$K=1$为CAPM，$K=3$为包含市场、SMB和HML的Fama-French（1993）三因子模型（简称FF3），$K=4$为Carhart（1997，“FFC4”）加入MOM的模型，$K=5$为Fama-French（2015，“FF5”）加入RMW和CMA的五因子模型，$K=6$（“FFC6”）在FF5基础上加入MOM。表4.2所有模型通过设定${\Gamma }_{\alpha }=0$（IPCA）或时序回归中省略截距项施加零截距限制。

表4.2报告了基于同期因子实现的总$R^2$、预测$R^2$（用因子平均风险溢价替代实现值）及各模型估计参数数量（$N_p$）。这些统计量为样本内计算。${}^4$对个股而言，可观测因子模型的总$R^2$略高于IPCA。但可观测因子模型参数数量远超IPCA。在11,452只股票、37个工具变量、599个月的样本中，可观测因子模型参数数量是IPCA的18倍（$\approx 11452/(37+599)$）！简言之，IPCA以约95%更少的参数提供了与领先可观测因子模型相似的股票系统性风险描述。同时，IPCA对股票风险补偿的描述显著更准确（如预测$R^2$所示）。对特征管理组合而言，可观测因子模型的总$R^2$与预测$R^2$均逊于IPCA。

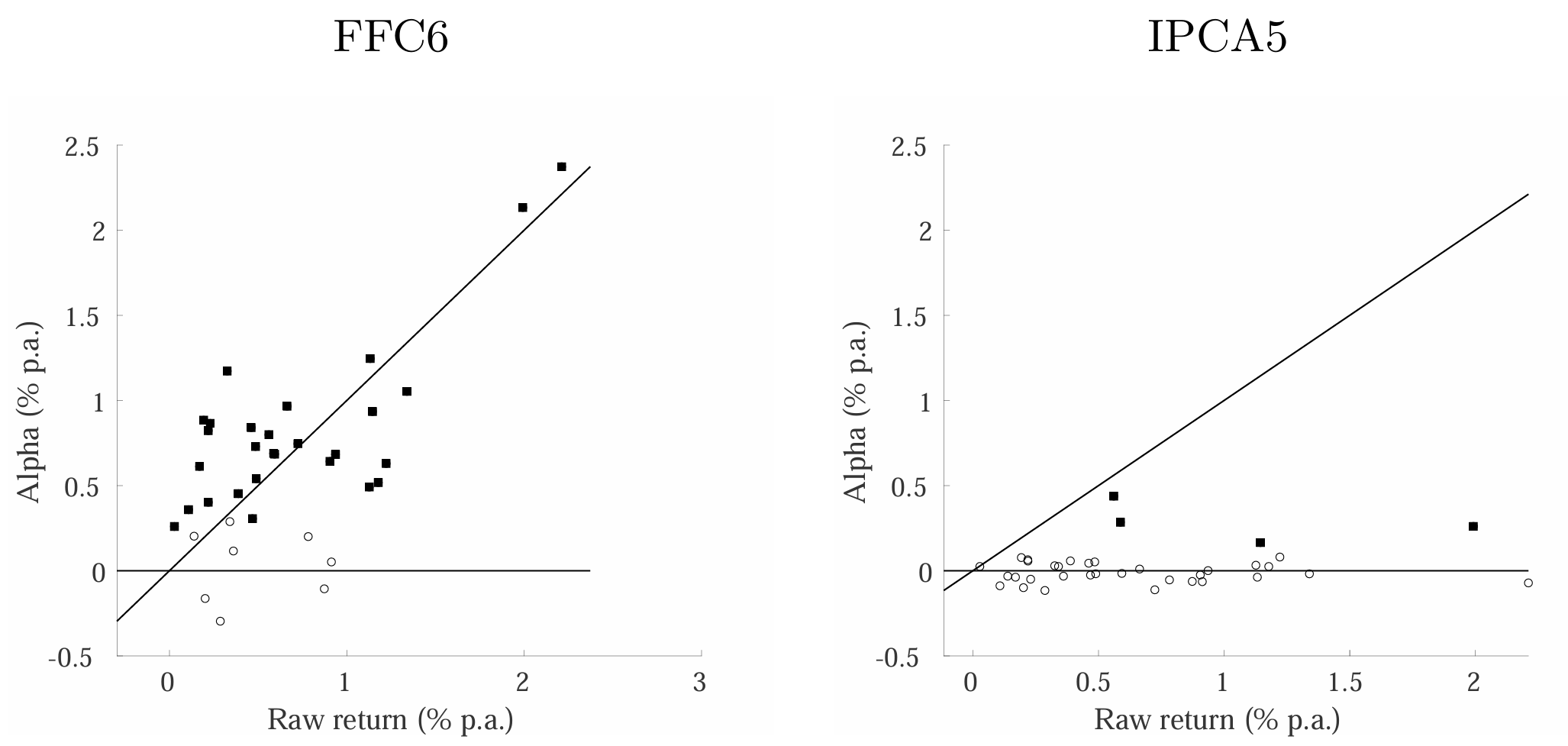
图4.2：特征管理组合的Alpha

说明：左右两图分别报告特征管理组合相对于FFC6模型与IPCA五因子模型的Alpha，横轴为组合原始平均超额收益。$t$统计量大于2.0的Alpha用实心方块表示，不显著的Alpha用空心圆圈表示（源自Kelly等, 2020b的图1）。

图4.2比较了37个特征管理"异象"组合的平均定价误差。${}^5$左图显示FFC6模型的组合Alpha与原始平均超额收益，叠加45度线。$t$统计量超过2.0的Alpha用实心方块表示，不显著的用空心圆表示。29个组合在FFC6模型下Alpha显著，且沿45度线聚集，表明其平均收益基本未被可观测因子解释。右图为五因子IPCA设定的条件Alpha时序均值。四个组合的条件Alpha显著非零但经济意义较小。图4.2支持IPCA潜在因子设定在定价各类股票组合方面优于可观测因子资产定价模型的结论。

${}^4$ Kelly等（2020b）显示IPCA样本外高度稳健，而可观测因子或PCA等模型样本外恶化更严重。
${}^5$为可比性，组合经调整符号与缩放，使其均值为正且年化波动率为10%。

IPCA框架已被用于研究各类市场的横截面资产定价，包括国际股票（Langlois, 2021; Windmueller, 2022）、公司债（Kelly等, 2021）、股指期权（Büchner和Kelly, 2022）、个股期权（Goyal和Saretto, 2022）及货币（Bybee等, 2023a）。该框架还被用于理解价格趋势信号的利润（Kelly等, 2021）及资产定价模型的叙事基础（Bybee等, 2023b）。

4.4 复杂因子模型

多篇论文研究了潜在条件因子模型中工具化贝塔设定(4.8)的推广形式。IPCA可视为基于可观测特征数据的风险暴露线性近似。虽然许多资产定价模型预测预期收益与状态变量间存在非线性关联，但理论文献对筛选条件变量与函数形式的指导有限。机器学习的兴起使我们能够用一系列非线性模型瞄准这种函数形式模糊性。

早期研究中，Connor等（2012）和Fan等（2016b）通过将贝塔视为条件特征的非参数函数（但与IPCA不同，为简化处理假设特征随时间固定）允许非线性贝塔设定。Kim等（2020）采用该框架研究对冲因子风险的"套利"组合行为。

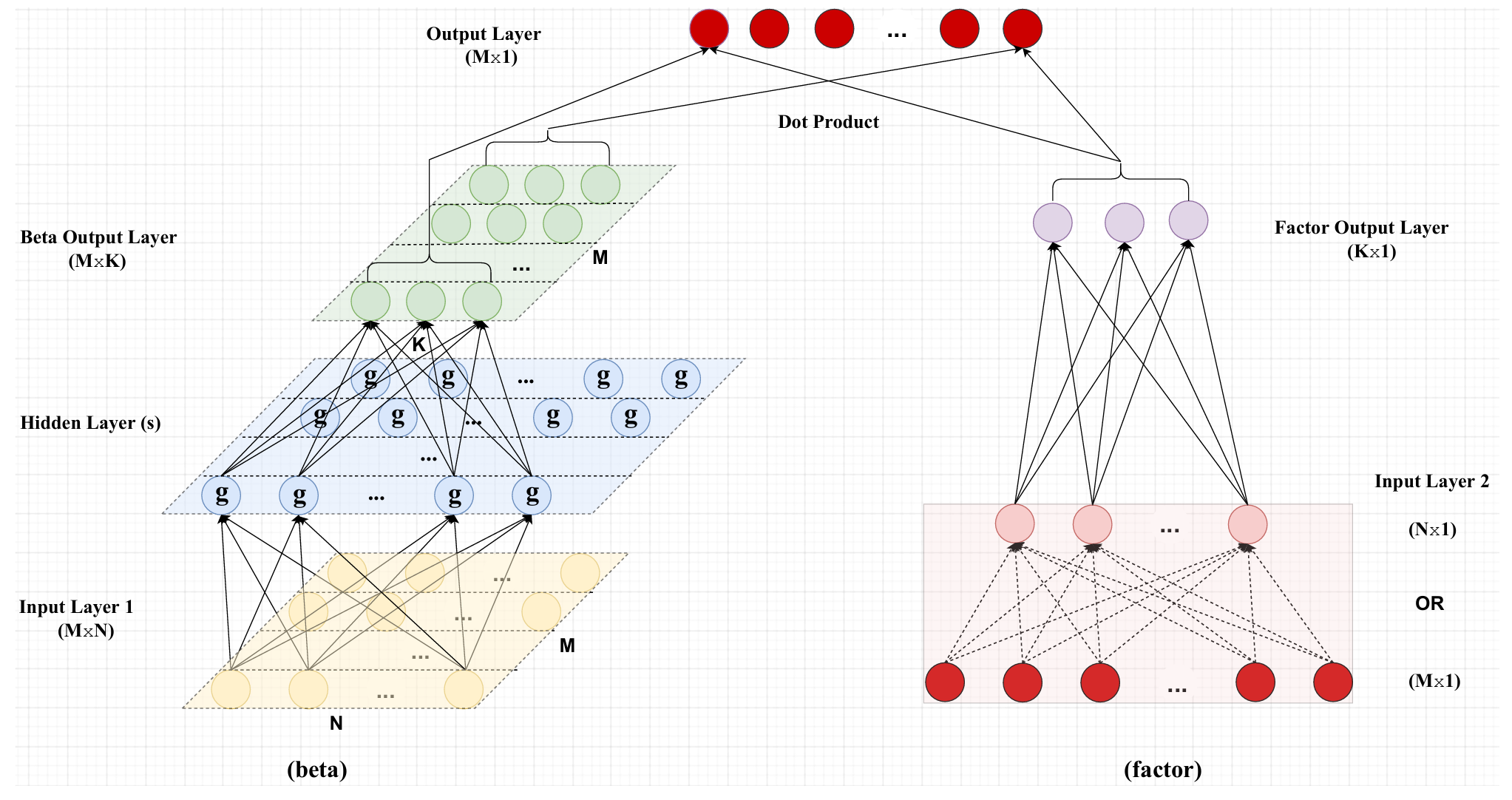
图4.3：条件自编码器模型

说明：本图为条件自编码器模型示意图，其中自编码器被增强以在因子载荷设定中纳入协变量。左侧描述因子载荷（绿色）如何通过隐藏层神经元的激活函数$g$依赖于输入层1的企业特征（黄色）。每行黄色神经元代表一只股票的特征向量。右侧描述对应因子。紫色节点为输入层2神经元的加权组合，可以是特征管理组合（粉红）或个股收益（红色）。前者通过预定义权重（无需估计）依赖个股收益（如虚线箭头所示）。无论哪种情况，有效输入均可视为个股收益，与输出层（红色）试图逼近的目标相同，因此该模型与标准自编码器精神一致。来源：Gu等（2020a）。

Gu等（2020a）通过允许贝塔为特征的神经网络函数扩展IPCA模型。图4.3展示了其"条件自编码器"（CA）模型结构，与(4.8)的不同在于通过非线性激活函数传播输入数据（工具变量$Z_t$）。CA是首个明确考虑风险-收益权衡的股票收益深度学习模型。Gu等（2020a）表明CA的总$R^2$与IPCA相似，但预测$R^2$显著优于IPCA。换言之，CA更准确地描述了资产条件性因子风险补偿。

Gu等（2020a）是高复杂度模型，其强劲实证表现暗示因子模型中复杂度的益处，类似于Kelly等（2022a）在预测模型中的发现。Didisheim等（2023）形式化这一思想并证明因子定价中复杂度的优势。他们围绕条件随机贴现因子（SDF）展开分析，SDF通常可表示为风险资产的组合：

$$M_{t+1}=1-w(X_t{)}^{\prime }{R}_{t+1},\text{\hspace{1em}(4.9)}$$

其中$R_{t+1}$为$N$个资产超额收益向量。$N$维向量$w(X_t)$包含SDF的条件组合权重，$X_t$代表跨越$t$时刻信息集的条件变量。在未知其函数形式时，$w()$可用机器学习模型近似：

$$w(X_t)\approx \sum _{p=1}^P{\lambda }_p{S}_p(X_t)$$

其中$S_p(X_t)$为$X_t$的某种非线性基函数，近似参数数量$P$较大。SDF的机器学习模型可解释为具有$P$个因子的因子定价模型：

$$M_{t+1}\approx 1-\sum _p{\lambda }_p{F}_{p,t+1},\text{\hspace{1em}(4.10)}$$

其中每个"因子"$F_{p,t+1}$为使用非线性资产"特征"$S_p(X_t)$作为权重的管理组合。Didisheim等（2023）的主要理论结果表明，资产定价模型中因子越多越好。在此设定下，增加因子意味着更丰富地表示$X_t$中的信息，从而更好地逼近真实SDF。逼近精度的提升压倒了估计多参数的统计成本。因此，随着因子数量增加，预期样本外alpha下降。这种对复杂度优势的解释对传统APT观点（少量风险因子足以完整描述任何可交易资产的风险-收益权衡）构成挑战。这意味着即使无套利且SDF存在，由于SDF必须被估计，可能（事实上预期）会不断发现未被现有因子解释的新实证"风险"因子，且将这些因子加入定价模型将持续提升其样本外表现。

4.5 高频模型

日益丰富的可交易资产高频交易数据为估计单个资产风险及其相互依赖关系提供了独特机遇。Andersen和Bollerslev（1998）、Andersen等（2001）及Barndorff-Nielsen和Shephard（2002）提出的波动率与协方差的简单非参数度量，早期展示了如何利用丰富及时的日内价格数据更好理解资产市场波动。高频测度的使用有助于解决研究低频时间序列的几个挑战。例如，帮助研究者在最小假设下适应结构断裂与时变参数。此外，经典时间序列中对线性、平稳性、依赖性与异方差的许多标准假设对日内数据建模往往不必要。

我们梳理出两条近期文献脉络：采用机器学习技术估计高维协方差矩阵与利用高频数据改进波动率预测。

精确的协方差估计对成功构建组合至关重要。但由于维度灾难，估计大规模协方差矩阵是具有挑战性的统计问题。许多方法依赖各类正则化（Bickel和Levina, 2008a; Bickel和Levina, 2008b; Cai和Liu, 2011; Ledoit和Wolf, 2012; Ledoit和Wolf, 2004）改进估计。受APT启发，Fan等（2008）在可观测因子的严格因子模型下提出基于因子模型的协方差矩阵估计量，Fan等（2013）则提出具有潜在因子的近似因子结构方法。

当面板维度接近样本量时，高频环境下也需要因子结构。但低频与高频采样环境下的计量经济学技术本质不同。后者通常基于允许收益动态存在随机变异与跳跃的一般连续时间半鞅模型设定。Ait-Sahalia和Xiu（2019）发展了处理日内数据的非参数PCA渐近理论，为连续时间因子模型应用铺平道路。此外，Fan等（2016a）和Ait-Sahalia和Xiu（2017）基于连续时间因子模型开发了个股高频数据的大协方差矩阵估计量。

将高频风险测度文献与预期收益横截面文献结合是利用更丰富的风险信息更好理解风险-收益权衡的前沿方向。相关研究包括Bollerslev等（2016）在连续时间设定下计算个股相对于单一市场因子连续与跳跃成分的贝塔，但在离散时间框架下将这些估计与收益横截面关联。Ait-Sahalia等（2021）在统一连续时间框架下提供风险溢价推断，同时第一阶段允许多因子与时变贝塔，第二阶段将贝塔视为第一阶段估计成分，推广了Shanken（1992a）的经典推断方法。实证中，他们使用Ait-Sahalia等（2020）构建的每15分钟采样的Fama-French与动量因子研究日内收益的因子模型。

利用高频数据测度波动率的思想也催生了波动率预测的前沿方向。Corsi（2009）基于过去已实现波动率测度的异质自回归（HAR）模型成为学术研究与行业实践中领先的波动率预测模型。近期多篇论文探讨了波动率预测的机器学习策略，包括Li和Tang（2022）和Bollerslev等（2022）。但与机器学习预测直接转化为更高夏普比的收益预测分析不同，目前尚不清楚机器学习预测在多大程度上优于现有HAR模型的经济意义。这是文献中一个有趣的开放问题。

4.6 Alpha

本节讨论关于alpha检验与机器学习的文献。Alpha是预期收益中未被因子贝塔解释的部分，因此是模型依赖对象。由于经济理论通常过于简化而无法确定所有因子身份，且数据可能不足以数据驱动地推断真实因子，模型误设是区分alpha与因子风险暴露"公平"补偿的持续挑战。例如，估计的alpha可能是弱因子贝塔的表现，类似于回归中的遗漏变量问题。换言之，一个人的alpha可能是另一个人的贝塔。在潜在因子模型中，alpha与贝塔最终通过区分因子与 idiosyncratic 噪声的因子强度临界值来区分。

我们主要从无条件潜在因子模型视角分析alpha。聚焦无条件而非条件alpha是源于文献重点；聚焦潜在因子模型是因为我们认为潜在因子模型的误设问题较轻。

4.6.1 Alpha检验与经济重要性

实证资产定价的长期焦点是所有alpha等于零的零假设${\mathbb{H}}_0:{\alpha }_1={\alpha }_2=\dots ={\alpha }_N=0$。这是区别于后文将讨论的多重假设alpha检验问题的单一假设。拒绝${\mathbb{H}}_0$被解释为资产定价模型误设或测试资产错误定价的证据（可能误认为是Ross（1976）APT的违背）。

著名的GRS检验（Gibbons等, 1989）是针对低维可观测因子模型的卡方检验。Fan等（2015）与Pesaran和Yamagata（2017）提出了相同零假设但针对高维设定的检验。这是重要进步，因为它消除了原始GRS检验的限制（$T>N+K$），并在$N$较大时提升检验功效。虽然这些方法最初针对可观测因子模型提出，但可扩展至潜在因子模型。事实上，Giglio等（2021a）利用(4.4)和(4.6)给出的估计因子载荷与风险溢价构建$\alpha$的估计量：

$$\hat{\alpha }=\frac{1}{T}\sum _{t=1}^T{R}_t-\hat{\beta }\hat{\gamma }.\text{\hspace{1em}(4.11)}$$

他们还推导了$\hat{\alpha }$的必要渐近展开，为潜在因子模型中的alpha检验奠定基础。

GRS检验统计量基于$({\mathbf{S}}^{\ast }{)}^2={\alpha }^{\prime }{\Sigma }_{ϵ}^{-1}\alpha$，可解释为零因子暴露组合的最优夏普比率平方。估计该夏普比是一回事，实施交易策略实现它是另一回事。即，GRS类检验中拒绝零alpha假设并不意味着拒绝具有经济重要性。任何对alpha经济重要性的有意义的量化都应考虑潜在套利者交易策略的可行性。从资产定价研究角度，以经济术语评估统计拒绝更有价值；对从业者也更相关。${}^6$

${}^6$ 如Shanken（1992b）所言：
…通过描述观察到的预期收益偏差带来的投资机会，为"近似套利"的概念赋予实际内容…我相信，通过考察我们能用现有资产近似套利的程度，将学到更多。

APT假设套利者知道收益生成过程中的真实参数。若样本量足够大使得参数渐近显现且套利者（近似）如同知道真实参数般行为，该假设可能无害。问题在于，在APT设定中，套利者必须知道数量递增的alpha，因此横截面维度相对于典型样本量较大。因此，即使在大$T$极限下，假设套利者能学习alpha也不合理。

Da等（2022）重新审视APT并放松已知参数假设。在其设定中，套利者必须依赖样本量$T$的历史数据使用可行交易策略。对时间$t$的任何可行策略$\hat{w}$，他们定义该策略下一期条件夏普比为：

$$S(\hat{w}):=E({\hat{w}}^{\prime }{R}_{t+1}|{\mathcal{I}}_t)/\text{Var}({\hat{w}}^{\prime }{R}_{t+1}|{\mathcal{I}}_t{)}^{1/2},$$

其中${\mathcal{I}}_t$为$t$时刻信息集。他们证明$S(\hat{w})$满足：

$$S(\hat{w})\le (S(\mathcal{G}{)}^2+{\gamma }^{\prime }{\Sigma }_v^{-1}\gamma {)}^{1/2}+op(1),\text{\hspace{1em}(4.12)}$$

其中$S(\mathcal{G}{)}^2:=E(\alpha |\mathcal{G}{)}^{\prime }{\Sigma }_e^{-1}E(\alpha |\mathcal{G}),$ 当$N\to \infty$时，${\Sigma }_v$为因子协方差矩阵，$\mathcal{G}$为由$\{(R_s,\beta ,V_s,{\Sigma }_e):t-T+1\le s\le t\}$生成的信息集。

值得注意的是，${\gamma }^{\prime }{\Sigma }_v^{-1}\gamma$为最优因子组合的夏普比率。因此，对任何因子中性策略$\hat{w},$ 即${\hat{w}}^{\prime }\beta =0,$

$$S(\hat{w})\le S(\mathcal{G})+op(1).\text{\hspace{1em}(4.13)}$$

该结果表明，$\alpha$的后验估计决定了最优可行夏普比率，并对统计套利利润施加上限。任何机器学习策略，无论简单复杂，都需遵守该可行夏普比率边界。

通常$E(S(\mathcal{G}{)}^2)\le E((S^{\ast }{)}^2)$，当且仅当$E(\alpha |\mathcal{G})=\alpha$几乎必然时等号成立。$S(\mathcal{G})$来自可行策略，$S^{\ast }$可称为不可行最优夏普比率。

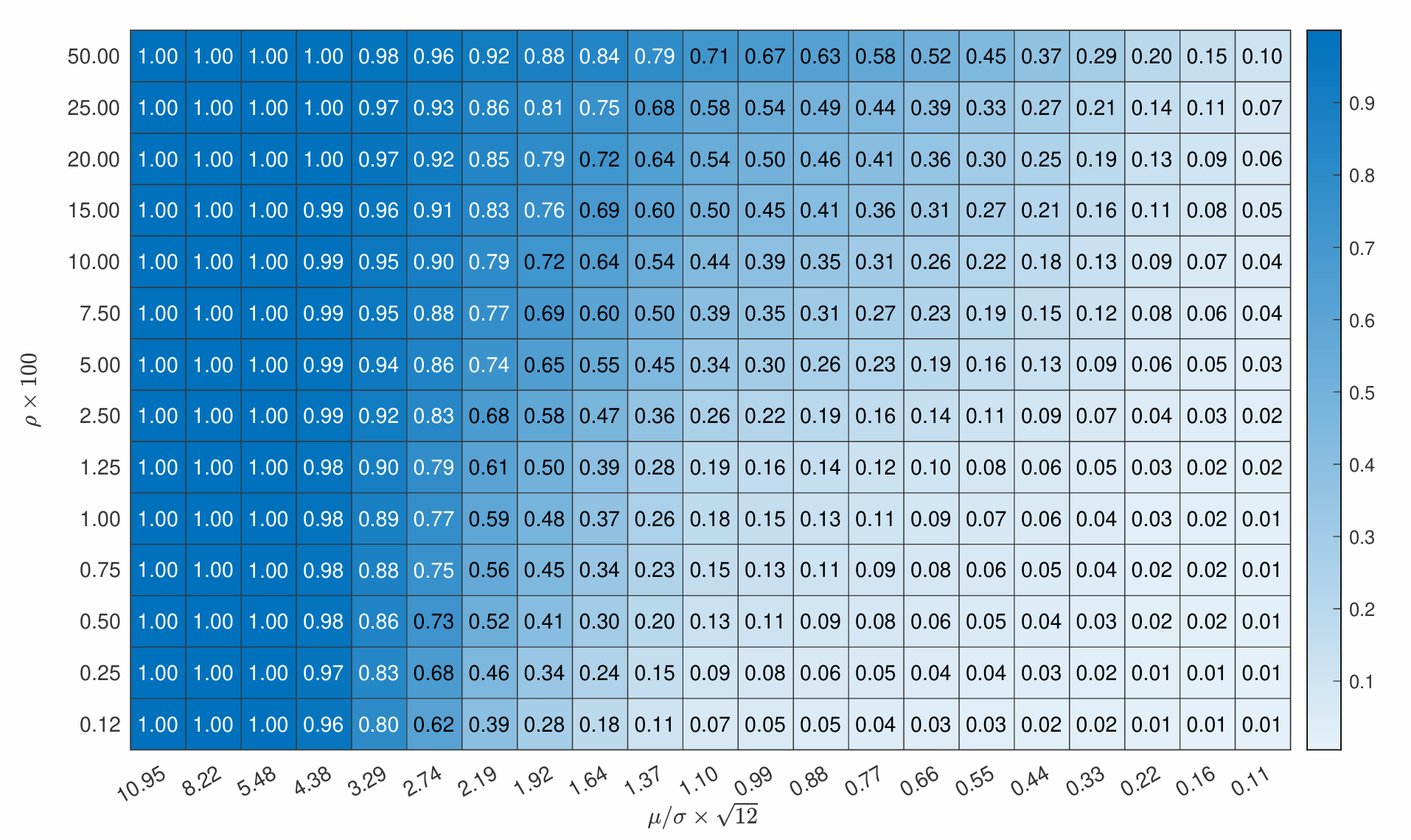
图4.4：$S(\mathcal{G})$与$S^{\ast }$比率

说明：本图报告可行与不可行套利组合最优夏普比率之比。模拟设定基于简单模型，其中仅$100\times \rho \%$资产具有非零alpha，每项对应年化夏普比率$\mu /\sigma \times \sqrt{12}$。来源：Da等（2022）。

可行与不可行策略间的"夏普比率缺口"表征统计学习难度。若学习困难，缺口较大。图4.4数值展示了假设收益生成过程中$\alpha$以概率$1-\rho$取零、以$\rho /2$概率各取$\mu$或$-\mu$时的两个夏普比率之比。残差协方差矩阵${\Sigma }_{ϵ}$为对角阵，方差为${\sigma }^2$。在此类数据生成过程中，$\mu /\sigma$表征$\alpha$强度（相对于噪声），$\rho$表征其稀缺性。图4.4通过变化$\mu /\sigma$和$\rho$展示不同生成过程中套利者表现的角色。当$\mu /\sigma$增加，alpha足够强且易于学习，夏普比率缺口较小。alpha稀缺性作用较弱，但更普遍的alpha也导致较小缺口。

Da等（2022）展示了如何量化不可行与可行夏普比率间的缺口。他们基于27因子模型评估APT，其中采用16个特征与11个GICS行业哑变量作为可观测贝塔。1975年1月至2020年12月测试样本的不可行夏普比率估计超过2.5，是机器学习策略实现的约0.5可行夏普比率的四倍以上。可行夏普比率（扣除交易成本前）低于0.5的事实表明APT实证表现良好。理论上，若套利者面临更多统计障碍（如模型误设、非稀疏残差协方差矩阵等），可行与不可行夏普比率间的缺口会进一步扩大。

4.6.2 多重检验

自CAPM提出以来，金融经济学界集体搜寻"异象"——即对CAPM具有alpha的组合。部分异象（如规模、价值等少数）已被吸收进基准模型（Fama和French, 1993; Fama和French, 2015）。当研究者检测到相对于现行基准模型的alpha时，会提出新异象。Harvey等（2016）综述文献并整理出300多个已记载异象。他们提出重要批评：异象搜寻工作评估新异象显著性时未能妥善处理多重假设检验问题。${}^7$

${}^7$更广泛地，Harvey（2017）等指出金融研究者因未报告检验、未考虑多重检验及促进"p值操纵"的职业激励而从分析得出错误结论的倾向。

此处的多重检验指同时检验一组零假设：${\mathbb{H}}_0^i:{\alpha }_i=0$, $i=1,2,\dots ,N$。该问题与前述检验单一零假设${\mathbb{H}}_0:{\alpha }_1={\alpha }_2=\dots ={\alpha }_N=0$有本质不同。多重检验易出现错误发现问题，因为部分个体alpha检验仅因偶然性而看似显著，导致错误拒绝零假设。

设$t_i$为检验零假设${\mathbb{H}}_0^i$的统计量。当$|t_i|>c_i$时拒绝${\mathbb{H}}_0^i$，$c_i$为预设临界值。令H0⊂{1,...,N}\mathcal{H}_0 \subset \{1, ..., N\}H0​⊂{1,...,N}表示真实零假设的索引集。$\mathcal{R}$为样本中总拒绝数，$\mathcal{F}$为错误拒绝数：

F=∑i=1N1{i≤N:∣ti∣>ci且i∈H0},R=∑i=1N1{i≤N:∣ti∣>ci}.\mathcal{F} = \sum_{i=1}^{N} 1\{i \leq N : |t_i| > c_i \text{且} i \in \mathcal{H}_0\}, \quad \mathcal{R} = \sum_{i=1}^{N} 1\{i \leq N : |t_i| > c_i\}.F=i=1∑N​1{i≤N:∣ti​∣>ci​且i∈H0​},R=i=1∑N​1{i≤N:∣ti​∣>ci​}.

$\mathcal{F}$与$\mathcal{R}$均为随机变量，但$\mathcal{R}$可观测而$\mathcal{F}$不可。

对预定水平$\tau \in (0,1)$（如5%），单个检验确保每检验错误率以$\tau$为界：$\mathbb{E}(\mathcal{F})/N\le \tau$。即错误拒绝的期望数量可达$N\tau$。为控制错误拒绝，另一种方案是选择更大临界值控制族错误率（FWER）：$\mathbb{P}(\mathcal{F}\ge 1)\le \tau$。但该方案在实践中过于保守。第三种方案由Benjamini和Hochberg（1995）提出，直接控制错误发现率（FDR）：FDR $\le \tau$，其中错误发现比例（FDP）及其期望FDR定义为FDP = F/max⁡{R,1}\mathcal{F}/\max\{\mathcal{R}, 1\}F/max{R,1}与FDR = E(FDP)。

虽然资产定价文献早意识到一般数据窥探问题（Lo和MacKinlay, 1990; Sullivan等, 1999），但早期提案建议替代单一零假设，如${\mathbb{H}}_0:{\max }_i{\alpha }_i\le 0$或${\mathbb{H}}_0:\mathbb{E}({\alpha }_i)=0$（参见White, 2000; Kosowski等, 2006; Fama和French, 2010）。Barras等（2010）、Bajgrowicz和Scaillet（2012）及Harvey等（2016）是首批在资产定价背景下采用FDR或FWER控制方法遏制多重检验的研究。Harvey和Liu（2020）提出双重bootstrap方法控制FDR，同时考虑假阴性率与比值比。${}^8$ Giglio等（2021a）提出潜在因子模型中alpha的严格FDR控制推断方法，同步解决检验计数中的遗漏变量偏差、缺失数据与高维度问题。Jensen等（2021）提出贝叶斯分层模型实现多重检验校正，利用零alpha先验与因子联合行为，使因子alpha估计向先验收缩并相互借力。

${}^8$Chen等（2023）研究数百个因子，发现控制FDR后仅存2个独立异象因子。

归根结底，多重检验本质是统计问题。上述统计方法通常满足良好统计检验标准，如控制I类错误、错误发现率等。但代理人最关心的是经济表现。这两个目标通常冲突。Jensen等（2021）与Da等（2022）指出，作为alpha选择工具的多重检验常导致极端保守的交易策略，尽管其完美防范FDR。Jensen等（2021）证明，基于贝叶斯分层多重检验方法纳入因子的研究者，其组合表现显著优于使用更保守FDR控制方法的投资者。