力扣刷题 -- 101.对称二叉树
题目与示例
思路分析
对称二叉树,说白了就是镜像对称,要解决这道题,我们需要分析镜像的特点。
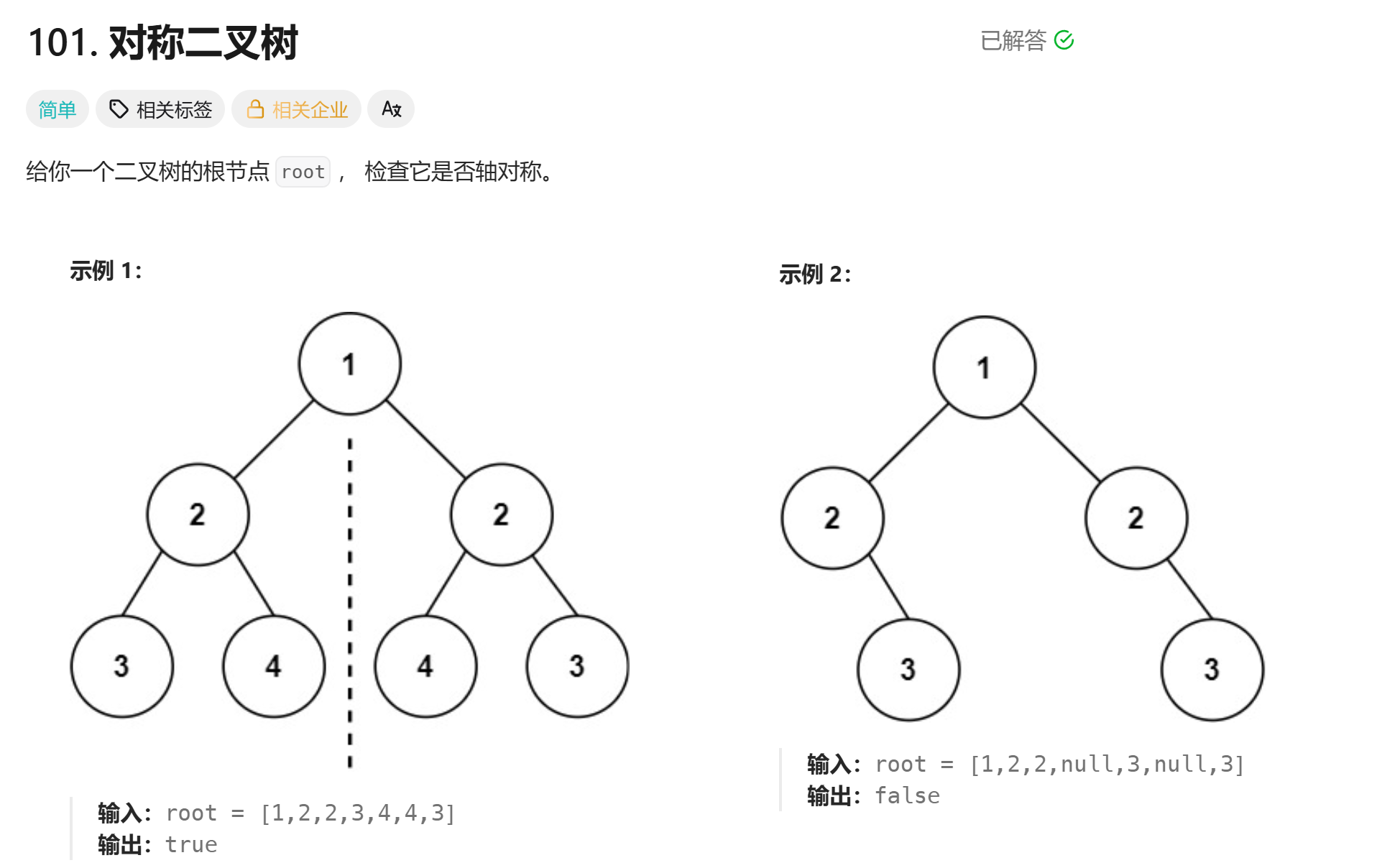
就以示例1来说:根结点的左孩子和右孩子的值相同;
再进一步看,欸发现 2 结点的左孩子和右侧 2 结点的右孩子是相同的;
左侧 2 结点的右孩子和 右侧 2 结点的左孩子相同;
欸,是不是我只要满足结点的左孩子的值和结点右孩子的值一样,结点右孩子和结点左孩子一样就可以解决这道题呢?
这里我们要注意传参,如果只有根结点那还挺好处理,如果左右子树都不为空,我们要分别处理2棵子树!!!
欸,有人问为什么要传2个参数?
我们知道二叉树的遍历是需要递归的,只要遇到递归结束的条件,才会依次销毁空间返回;只有左侧递归处理完,才能处理右侧,但在这里我们要两侧都遍历。
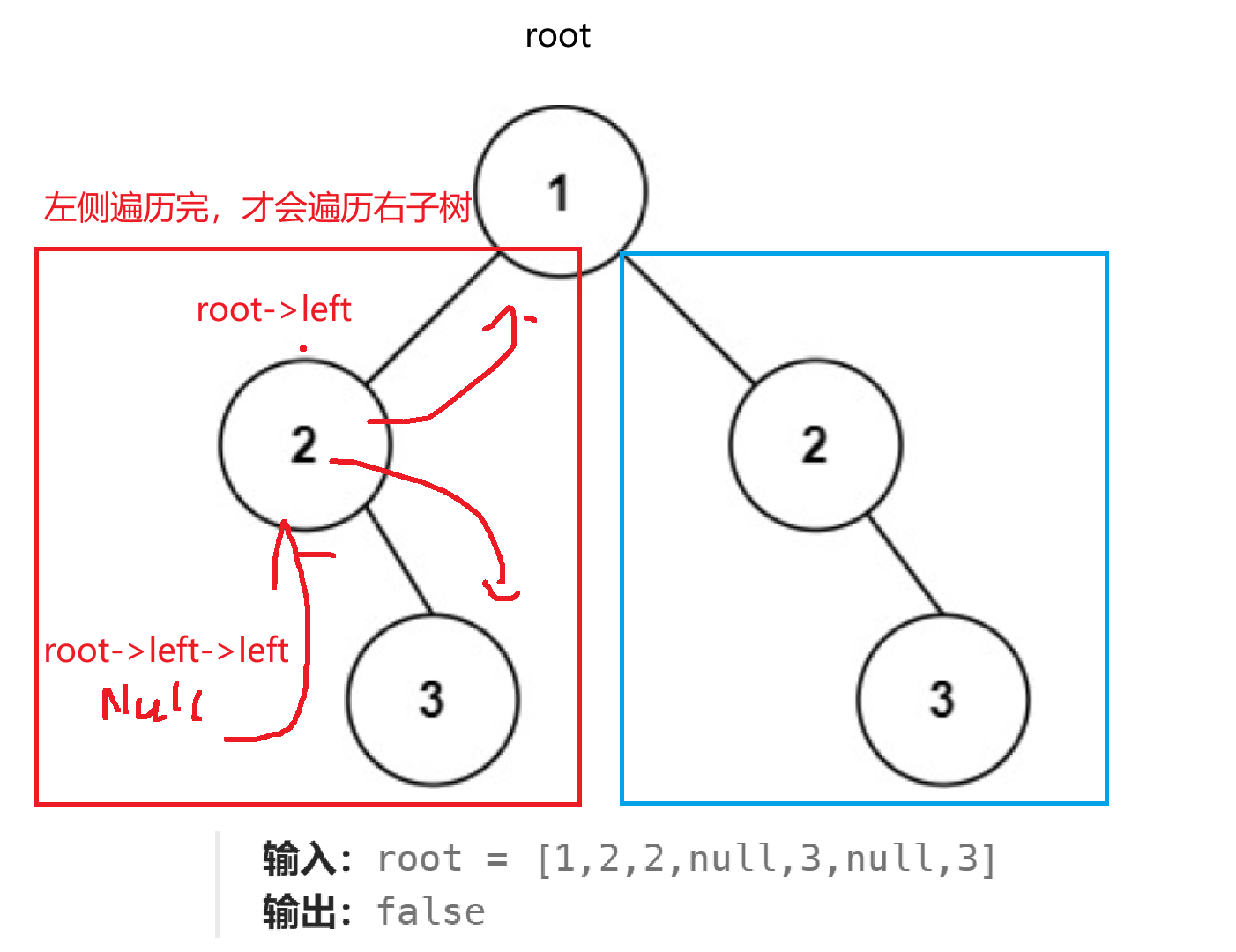
注意:有两种特殊情况
情况1:空树,属于对称的树;
情况2:树只有根结点,是属于对称的树;
情况3:有1棵子树为空树(即左子树为空但右子树不为空;左子树不为空右子树为空),不是对称的树。
千万不能漏掉这两种情况!!!
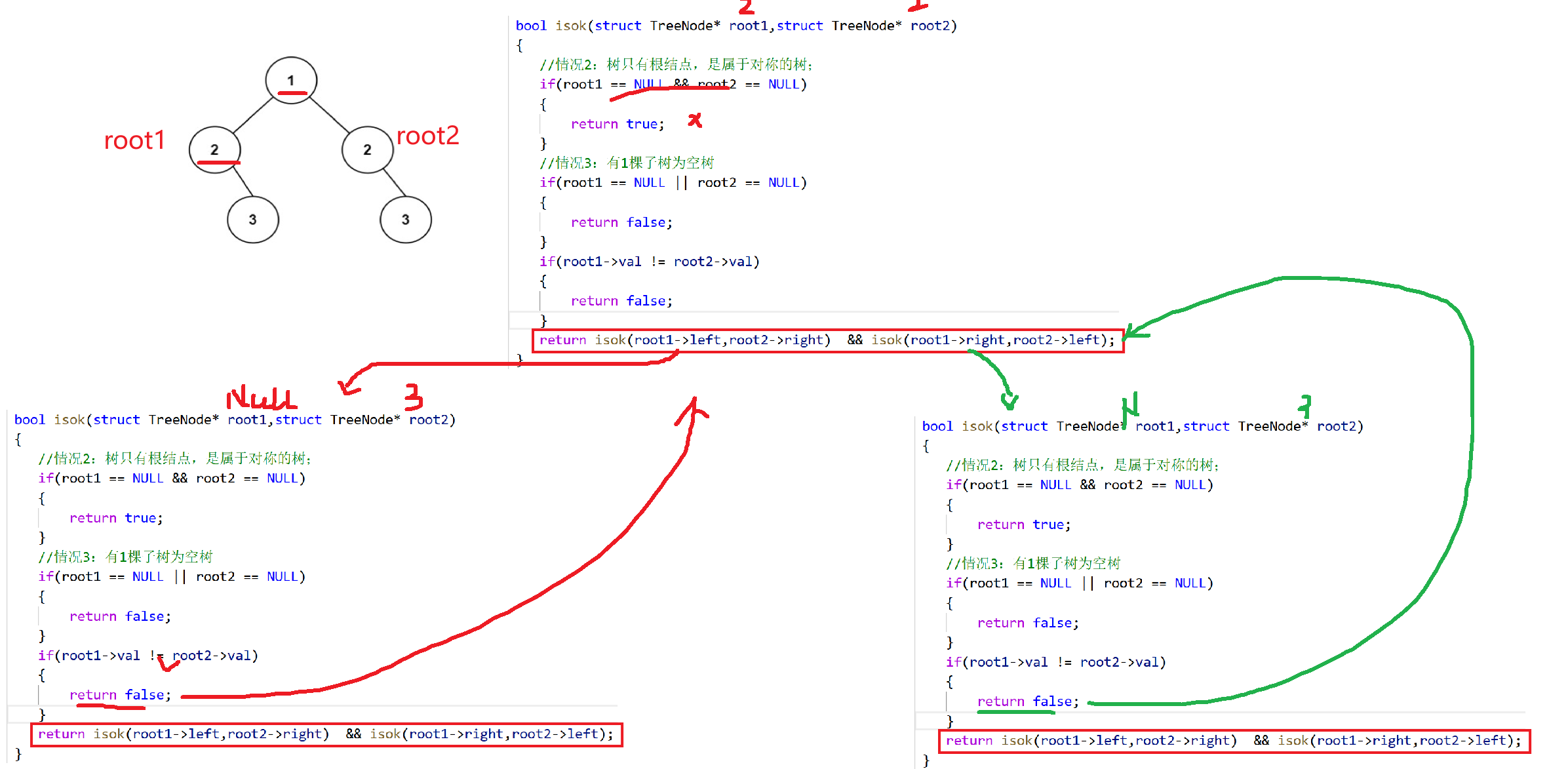
代码实现
typedef struct TreeNode TreeNode;//判断是否对称bool isok(struct TreeNode* root1,struct TreeNode* root2){//情况2:树只有根结点,是属于对称的树;if(root1 == NULL && root2 == NULL){return true;}//情况3:有1棵子树为空树if(root1 == NULL || root2 == NULL){return false;}if(root1->val != root2->val){return false;}return isok(root1->left,root2->right) && isok(root1->right,root2->left);}
bool isSymmetric(struct TreeNode* root) {//情况1:空树if(root == NULL){return true;}return isok(root->left,root->right);
}