Agentic-R1 与 Dual-Strategy Reasoning
我们在平时用reasoning模型的一个问题,有时候明明可以调用外部工具的时候,比如计算器能快速做一个平方题,它非得磨磨叽叽算好几遍,然后一顿口high,如果数大了,大概率还会算错,根源是其实LLM不懂数学
我以前写过一个文章
LLM到底会解数学题吗?
也会有人反驳我deepseek R1前一阵做的数学多厉害,但是那个是lean,你如果lean是啥都不懂,那就别唠了
另外昨天的时候OAI也拿了IMO的金牌,这两个事情本身都值得称赞,但是从本质上也改变不了LLM就不合适做复杂数学的原因
当然除了数学以外还很多问题,并不是推理步骤越多越好,比如一些偏向事实性的问题,你调一个api或者mcp啥的更好
所以就有了如下这个论文

又是CMU的,CMU的最近论文质量都还可以
这论文讲的啥意思呢?
一. 它的目标
1.问题背景
数学和推理任务:长链式思维( long-CoT)模型在复杂推理如数学问题上其实已经比以前很呦进步了,但计算慢、尤其是文本推理链容易出错,多轮对话更是容易attention稍微一个飘逸recall,基本就容易出错
工具增强(Tool-augmented)agent:通过代码等工具可以实现高效、准确的计算,但对于更“抽象”的推理能力有限,你除非跟它说的很彻底的细化,要不写不清楚。
2. 主要创新
DualDistill 框架:首次通过“分步解轨迹拼接+多教师蒸馏”的方式,把两种互补推理策略(工具增强/文本推理)融于一个学生模型,如图
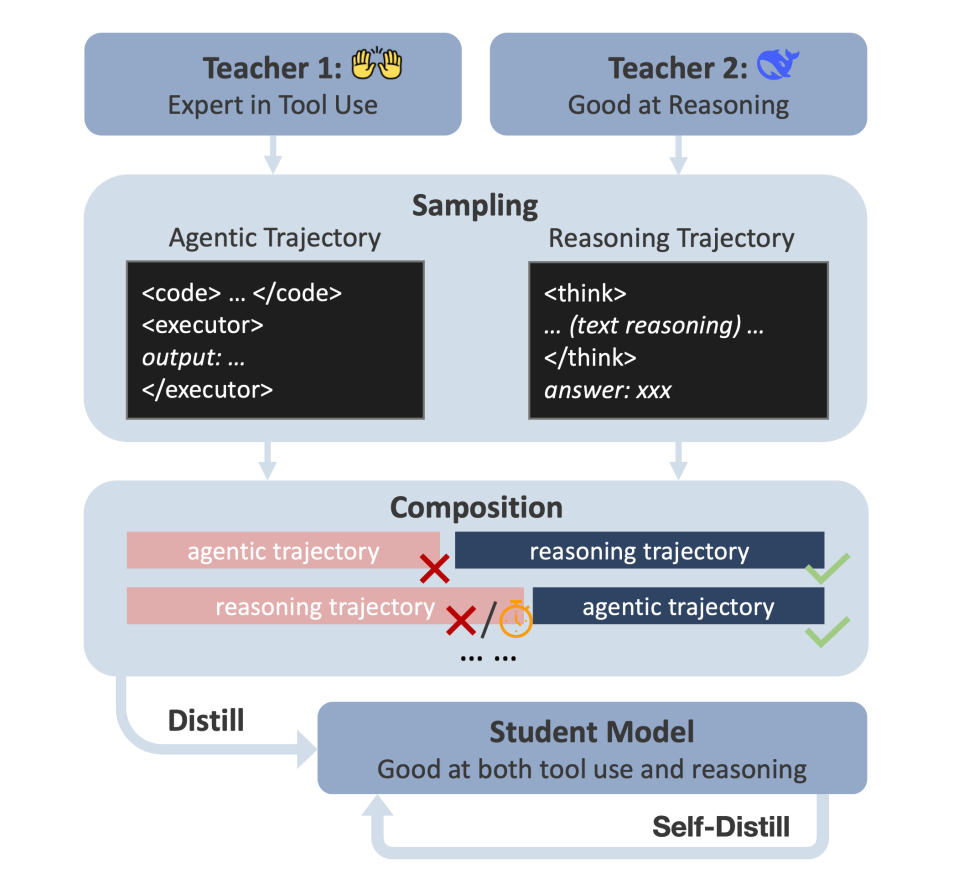
Agentic-R1 模型:能动态选择合适的推理策略,对算术题自动用代码、对抽象题用自然语言推理。
二 方法机制与细节
1. 轨迹拼接
如图取两个teacher:一个Agentic(工具+代码,基于OpenHands/Claude-3.5),一个Reasoning(文本推理,基于Deepseek-R1)。
-
每道训练题由老师A解一步、B基于A的输出再解一步,根据逐步解答的正确与否拼接成多段式“复合轨迹”(有手工设计的转场语句,比如“换用代码试试”)。
-
最终学生模型通过模仿这些解决轨迹来学习如何“选策略”。
2. 训练样本筛选
-
并不是所有题都适合工具或长文本,需要精选一批区分度明确的数据(如大型数值计算适合工具,少量题适合文本)。
-
数据主要来自DeepMath等大规模数学数据集,筛选和过滤过程(一会讲)
3. 自蒸馏机制
-
因为学生模型大小/能力有限,往往对部分问题策略选择不佳,容易“过用工具”或操作失误。
-
增加自蒸馏步骤:让学生模型自己生成多条解题路线,再用教师进行校验或修正,把有效策略强化、无效例子修正。
4. 目标与评价
-
希望学生模型不仅能把师傅的策略拼接学到位,还能实际提升数学推理准确率和效率,并自动学会“何时用工具、何时用文本”。
其实思路挺简单和清晰的,大部分都好理解,我就讲两个值得讲的点
第一 小模型(学生)应该学习到什么玩意?
举个例子(论文例子不咋好,我举个简单易懂的)
假定题目
“计算 1 到 100 的和。”
1. Teacher A(文本推理 CoT,Reasoning Teacher)
输出(纯文本推理 CoT):
<think>
我们要求 1 到 100 的和。
经典公式:前 n 项和 = n*(n+1)/2。
代入 n=100 得:100*101/2 = 5050。
</think>
<answer>5050</answer>
经典公式:前 n 项和 = n*(n+1)/2。
代入 n=100 得:100*101/2 = 5050。
</think>
<answer>5050</answer>
2. Teacher B(工具推理,Agentic Teacher)
输出(工具/代码):
<think>
我们可以用代码快速计算 1 到 100 的和。
</think>
<code>
print(sum(range(1, 101)))
</code>
<executor>
输出结果: 5050
</executor>
<answer>5050</answer>
</think>
<code>
print(sum(range(1, 101)))
</code>
<executor>
输出结果: 5050
</executor>
<answer>5050</answer>
3. 轨迹拼接机制实例
假设这样拼接的场景:
-
Teacher A(文本推理)先解题,但因为某个细节笔误写错公式,没得出正确结果(假设本次A出错)。
-
Teacher B(代码)基于A的推理后补救,代码执行得出正确答案。
于是我们拼出了一条复合训练轨迹,并加入人工设计的“策略切换”提示:
<think>
我们要求 1 到 100 的和。
经典公式用错了,算出来不是正确答案。(假如这里A写错,得个0出来)
</think>
Wait, the text reasoning result seems off, let's try code reasoning.
<think>
我们可以用代码快速计算 1 到 100 的和。
</think>
<code>
print(sum(range(1, 101)))
</code>
<executor>
输出结果: 5050
</executor>
<answer>5050</answer>
重点提示:中间的句子是论文里那种transition segment
比如
Wait, the text reasoning result seems off, let's try code reasoning.
这是人给加上去的,为啥要这么干呢?
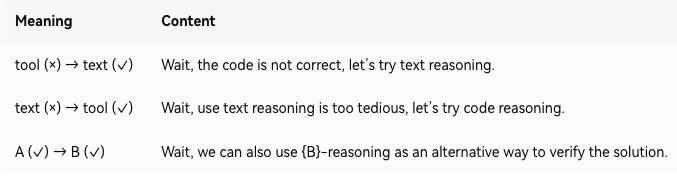
目的就是给模型知道啥情况你用reasoning好使,啥情况你直接调tool更牛b
这个实现也简单就是比如一个template通过随便写点代码给条件话的加上去,拼接两个老师的输出,交给学生sft的时候自己去认
for (x, a) in training_set:y1 = teacher_A.solve(x)y2 = teacher_B.solve(x, y1)g1 = grader(y1, a)g2 = grader(y2, a)if g1==0 and g2==1:# 文本错,工具对trajectory = y1 + "Wait, use text reasoning is too tedious, let’s try code reasoning." + y2elif g1==1 and g2==0:# 工具错,文本对trajectory = y1 + "Wait, the code is not correct, let’s try text reasoning." + y2elif g1==1 and g2==1:# 两个都对trajectory = y1 + "Wait, we can also use CODE-reasoning as alternative to verify." + y2# 把trajectory作为学生模型的finetune训练样本training_examples.append(trajectory)
好,我们总结一下:
-
这样一整条轨迹,前半部分是文本逐步思考,后半通过代码调用计算器给出答案,中间通过"Wait, ..."人工转场语句衔接。
-
论文的“轨迹拼接”过程,就是通过类似的例子,组合出多样推理路径,让学生模型通过蒸馏学会什么时候切换、怎么切换。
-
这让模型既知道遇到算术/复杂题可以用工具,也明白纯文本推理论证也不可少,更能融合两者优点。
第二个问题如何定义数据
题目筛选与划分(Problem Filtering Heuristics)
分为“Agentic-Favored Subset(适合用工具的子集)”和“Pure Reasoning-Favored Subset(适合用文本的子集)”两类:
一 Agentic-Favored Subset(工具优先)
主要按照两条规则筛选:
数值规模(Numerical Scale) :题目如果最终答案是整数且绝对值“大于1000”,这类题通常涉及大量复杂的算术运算、人答很繁琐,适合优先用工具(如代码计算)解决。
文本模型受限下的难度(Difficulty Under Constraints) :用文本推理模型(Deepseek-R1-Distill-7B),限定推理链最大长度(4096 tokens)解题。如果用这种方式还是解不对,那就判定为“文本推理难度大”——适合靠工具策略。
二 Pure Reasoning-Favored Subset(文本优先)
主要思路:选择那些即使用工具推理(agentic策略)也容易出错的题。这说明这些题工具不适合,还是文本分析更靠谱。
筛选方法:
让工具类模型尝试解题,如果工具策略依然出错,就纳入该子集。
最终处理:
以 DeepMath-103K 数据集为主(2025年大规模数学题万级集),先筛选,再两类子集数量平衡,保证训练时两种策略教师的题量近似对等。
这样确保学生模型训练时既能见到大量“典型用工具”的题,也见到“典型用文本”的题。
数据规模统计
全部筛选和合成后,最后的训练集一共2678条复合轨迹(即拼接后的优质“多步题解”)。
论文中提供了三种拼接类别(两步都对/一步对一步错等)及其数量统计。
举个例子:
举例1(工具优先):
“求一个整数 99999 的阶乘是多少?”
→ 显然答案很大不便人工算,纯文本不好写,直接用工具计算最合适。
举例2(文本优先):
“证明如果x+y是偶数,且x、y都是整数,则x和y同奇偶。”
→ 这种不算数值,主要靠纯文本逻辑推理,用代码没啥好处。
通过这种机制,模型能在训练时“观察”不同老师各自擅长和失误的题型,真正学会策略择优。
过滤过程中还会平衡两类题目数量,构成最终训练集。
开源了,大家想玩可以自己试试
https://github.com/StigLidu/DualDistill
