Day23| 39. 组合总和、40.组合总和II、131.分割回文串
39. 组合总和
与前面几题的区别是:
-
这道题中元素可以重复
-
用组合限制树的深度
回溯三部曲:
-
递归函数参数 集合candidates、目标值target、和sum、控制for循环的起始位置startIndex
-
递归终止条件 终止的·两个条件:sum大于target;sum等于target
-
单层搜索的逻辑 单层for循环依然是从startIndex开始,搜索candidates集合。
public class Solution {public IList<IList<int>> res=new List<IList<int>>();public IList<int> path=new List<int>();public IList<IList<int>> CombinationSum(int[] candidates, int target) {BackTracking(candidates,target,0,0);return res;}public void BackTracking(int[] candidates, int target,int sum,int startIndex){if(sum>target) return;if(sum==target){res.Add(new List<int>(path));return;}for(int i=startIndex;i<candidates.Length;i++){sum+=candidates[i];path.Add(candidates[i]);BackTracking(candidates,target,sum,i);sum-=candidates[i];path.RemoveAt(path.Count-1);}}
}40.组合总和II
这道题目和39.组合总和 (opens new window)如下区别:
-
本题candidates 中的每个数字在每个组合中只能使用一次。
-
本题数组candidates的元素是有重复的,而39.组合总和 (opens new window)是无重复元素的数组candidates
去重:
-
树枝去重:一个维度是同一树枝上使用过
-
树层去重:一个维度是同一树层上使用过(采用)
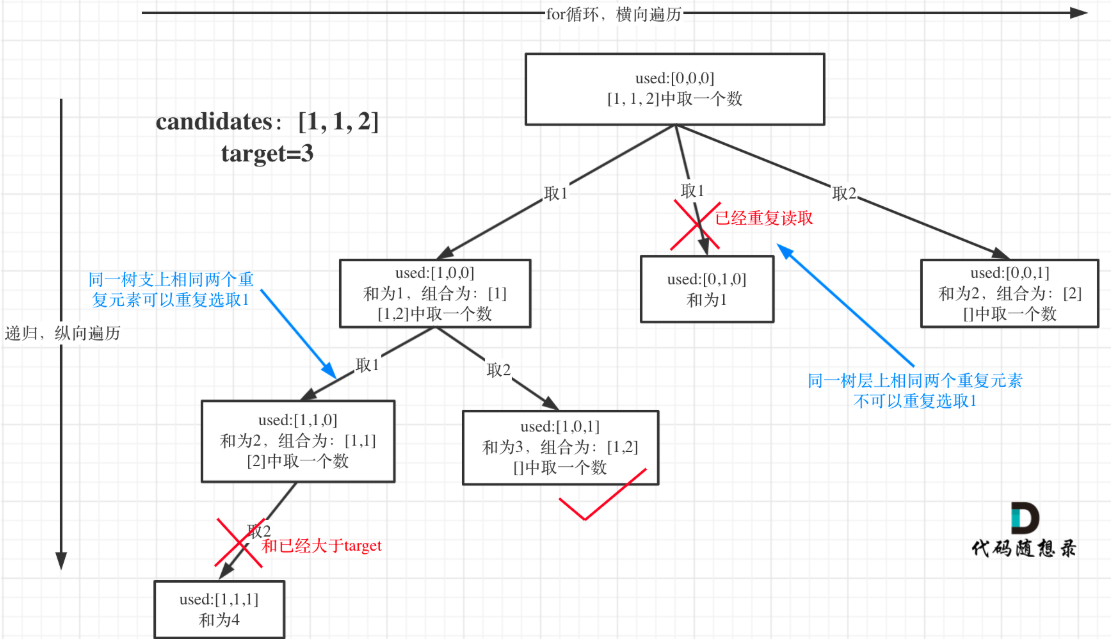
步骤:
-
排序输入数组
candidates: -
便于剪枝
-
便于发现重复数字并进行去重处理
-
使用回溯法进行组合搜索
-
每次递归遍历后续的数字(
i+1),避免重复使用 -
路径合法(和为 target)就加入结果
-
去重关键:跳过重复元素
-
在同一层 for 循环中,如果当前数字和上一个相同,跳过它
public class Solution {public IList<IList<int>> res = new List<IList<int>>(); // 存放最终结果集合public IList<int> path = new List<int>(); // 临时路径(当前组合)public IList<IList<int>> CombinationSum2(int[] candidates, int target) {Array.Sort(candidates); // 先排序,方便剪枝和去重Backtrack(candidates, target, 0, 0);return res;}public void Backtrack(int[] candidates, int target, int start, int sum) {if (sum == target) {res.Add(new List<int>(path)); // 如果和等于目标,加入结果return;}for (int i = start; i < candidates.Length; i++) {int cur = candidates[i];// 剪枝:当前数 + 现有和已经超过 target,后面更大直接跳过if (sum + cur > target) break;// 去重:同层中遇到相同元素,跳过(i > start 表示是“同一层”)if (i > start && candidates[i] == candidates[i - 1]) continue;// 做选择path.Add(cur);Backtrack(candidates, target, i + 1, sum + cur); // i + 1 表示不能重复选同一个元素path.RemoveAt(path.Count - 1); // 撤销选择(回溯)}}
}131.分割回文串
回文字符串(Palindromic String)是指从左到右读和从右到左读完全相同的字符串,其字符序列呈现 “对称” 特征
-
单个字符:
"a"、"5"、"#"(单个字符本身就是回文)。 -
两个字符:
"aa"、"22"、"##"(两个相同字符构成回文)。 -
多个字符:
-
英文:
"madam"( Madam 倒读仍是 Madam)、"level"( Level 倒读仍是 Level)。 -
中文:
"上海自来水来自海上"、"黄山落叶松叶落山黄"。 -
数字 / 符号:
"12321"、"#@#"。
🚀 核心算法:回溯 + 剪枝(判断是否是回文)
我们从左往右依次枚举字符串的切分点:
-
每次切一段子串
s[start..i]: -
如果是回文,就加入当前路径
path -
然后递归处理剩下的字符串
s[i+1..] -
直到走到字符串末尾,说明找到了一种可行方案,加入结果集
public class Solution{public IList<IList<string>> res=new List<IList<string>>();public IList<string> path=new List<string>();public IList<IList<string>> Partition(string s) {Backtracking(s,0);return res;}public void Backtracking(string s,int start){if(start==s.Length){res.Add(new List<string>(path));return;}for(int i=start;i<s.Length;i++){if(IsPalindrome(s,start,i)){path.Add(s.Substring(start,i-start+1)); // 加入路径Backtracking(s,i+1);path.RemoveAt(path.Count-1);}}}// 判断字符串s从left到right是否是回文private bool IsPalindrome(string s,int left,int right){while(left<right){if(s[left]!=s[right]) return false;left++;right--;}return true;}
}