Python应用指南:使用PyKrige包实现ArcGIS的克里金插值法
先了解什么是克里金插值?
克里金插值(Kriging interpolation)是一种基于统计学和空间相关性的高级空间插值方法,广泛应用于地理信息系统(GIS)、地质勘探、环境科学、气象学等领域。它由南非矿业工程师丹尼尔·克里金(Daniel Krige)提出,并由法国数学家乔治·马瑟伦(Georges Matheron)发展为一种严格的数学方法。其核心思想是:在空间分布的数据中,相邻位置之间的属性值往往具有一定的相似性,即空间自相关性。克里金插值正是利用这种空间相关性,通过构建变异函数模型(Variogram),对未知点的值进行最优无偏估计。克里金插值不仅考虑了已知点与未知点的距离关系,还结合了数据的整体空间结构特征,从而提供更精确且具统计意义的预测结果。
白话版:想象一下你有一块农田,想知道整个田地不同位置的土壤肥力情况,但你只能取样有限的几个点进行测量。如何根据这几个点的数据来推测其他未测量点的土壤肥力呢?这时候就可以使用克里金插值方法了。
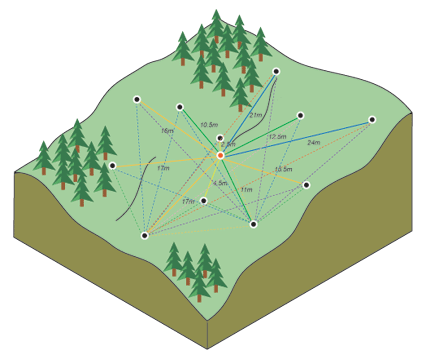
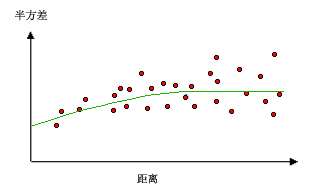
为了更好的理解计算原理,我们来看这张图,其中一个点被标记为红色,作为我们分析的焦点(也是缺失值点)。从这个红色点出发,到其他每个黑色数据点之间都有一条连线,并标明了两点间的距离,当我们计算红色点与所有其他点之间的属性差异(比如海拔高度或土壤湿度)时,会发现距离较近的点具有更小的差异,这表明它们的属性更加相似;而随着距离增加,这种相似性逐渐减弱,即两个位置的属性值差异增大。为了更好地理解和展示这一点,通常我们会将所有点对按照距离分组,并计算每组内属性差异的平均值,根据这些数据绘制出一张图表,其中横轴表示距离,纵轴表示属性差异的平均值。这样得到的图表被称为半变异函数云图。
简单来说,在半变异函数云图中,越靠左下角的位置代表的是距离近且属性值相似的点对,而向右上方移动,则意味着距离的增加,这些点对之间的属性值差异也越来越大,从而形象地展示了地理学中“地理位置越接近的事物往往越相似”的规律;
遇到问题:栅格数据转点集,再通过空间连接关联到网格或者不同尺度的网格时候,通常会因为数据尺度不一致或者数据本身有缺失导致部分网格缺失数据,这时候就需要通过补差值的方法进行对数据本身的补充;
那么我们直接进入实现方法:
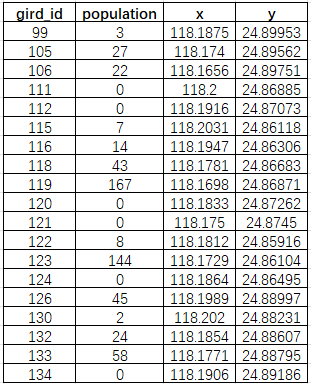
第一步:先把遇到缺失值的网格进行增加x,y数据,目的是赋予人口数据空间属性;
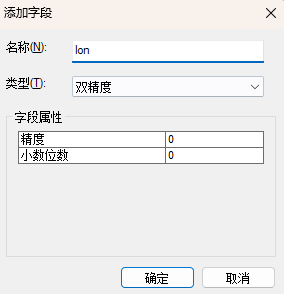
第二步:把表导出为文本或者csv表格,其他标签可以手动剔除,保留这四个标签即可,唯一id,方便进行表连接,缺失数据字段,这里是人口(population),x,y坐标;
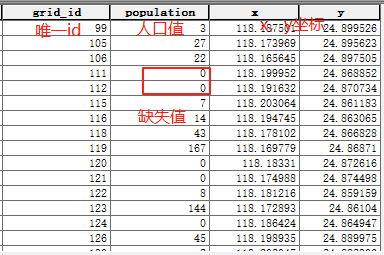
第三步:把表导出为文本或者csv表格,这个我们通过PyKrige 的这个克里金插值工具包来实现,arcgis的克里金插值的功能;
方法思路
- 读取原始数据(含坐标 x, y 和 population 值);
- 分离出已知点和未知点;
- 构建克里金模型并对未知点进行插值;
- 将插值结果替换原始数据中的空缺值(population=0)
- 输出并保存插值后的完整数据
完整代码#运行环境 Python 3.11
import pandas as pd
import numpy as np
from pykrige.ok import OrdinaryKriging
import matplotlib.pyplot as plt# 加载数据
file_path = r"C:\Users\Admin\Desktop\人口插缺失值表.csv"
data = pd.read_csv(file_path)# 提取已知点的坐标和对应的population值
known_points = data[data['population'] != 0][['x', 'y']].values
known_values = data[data['population'] != 0]['population'].values# 提取需要插值的点的坐标
unknown_points = data[data['population'] == 0][['x', 'y']].values# 使用pykrige进行普通克里金插值
OK = OrdinaryKriging(known_points[:, 0], known_points[:, 1], known_values, variogram_model='linear',verbose=False, enable_plotting=False)z1, ss1 = OK.execute('points', unknown_points[:, 0], unknown_points[:, 1])# 将插值结果填充回原数据
data.loc[data['population'] == 0, 'population'] = z1# 输出结果
print(data)# 保存结果到新的CSV文件
output_file_path = r"C:\Users\Admin\Desktop\插值后的人口数据_kriging.csv"
data.to_csv(output_file_path, index=False)print(f"插值完成并保存至: {output_file_path}")我们就可以得到了这么一张新的表格,表的输入和输出路径、名称可以根据自己的实际需求自行修改;
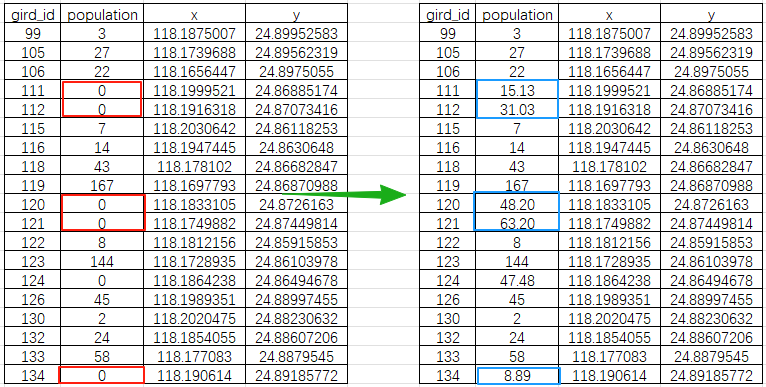
这里使用的是"linear",相似性随距离线性减少,通常用于表示简单、直接的空间自相关性,适用于那些表现出稳定的空间异质性且没有明显变程的数据集,当然也可以尝试其他模型如"spherical", "gaussian",直接在脚本里替换"linear"即可;
常见的变异函数模型
Spherical Model (球状模型)
- 描述:球状模型是最常用的变异函数之一,假设当两点间的距离超过某个范围(称为变程,range)后,数据值之间的空间自相关性变为零。在这个模型中,变异函数从原点开始线性增加,直到达到一个特定的距离(即变程),之后保持不变。
- 适用场景:适用于那些空间自相关性在一定距离后迅速消失的数据集。
Gaussian Model (高斯模型)
- 描述:高斯模型是一个平滑过渡的模型,表明即使在较远的距离上,数据值之间仍然可能存在一定的自相关性。与球状模型相比,高斯模型的变化更为渐进,没有明显的“跳跃”到一个恒定值的过程。
- 适用场景:适合于表现出连续和平滑变化趋势的数据集,例如地形高度或气候变量等。
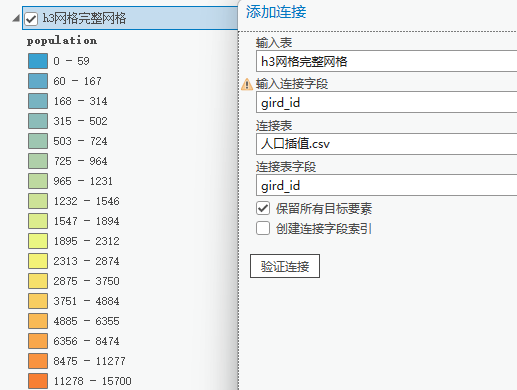
第四步:把生成的表导入arcgis,右键网格图层,添加连接,连接表字段选择"gird_id"字段,接下来符号系统选择"population"字段进行可视化即可;
这是数据插值前的人口分布图,可以看到因为数据尺度的不匹配导致,网格产生较多的空值,色彩过渡也不自然;
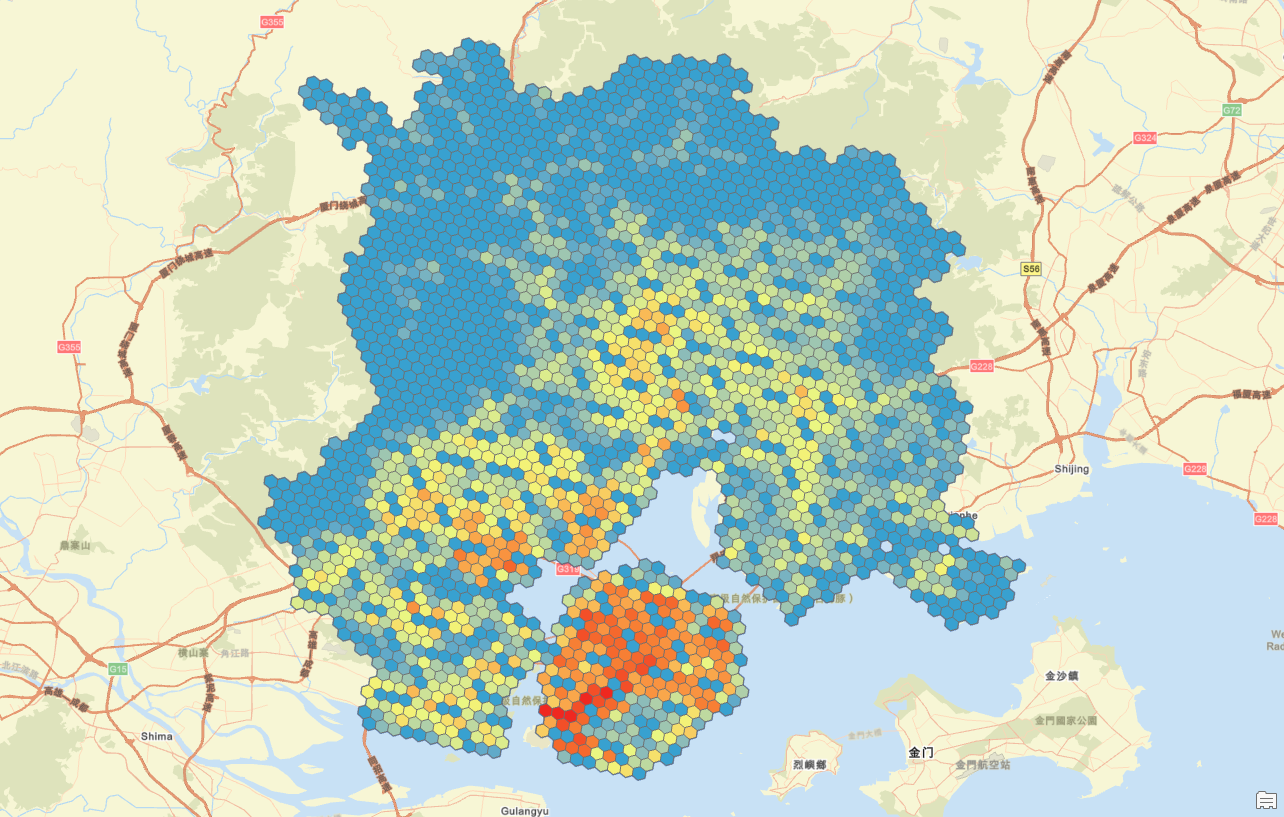
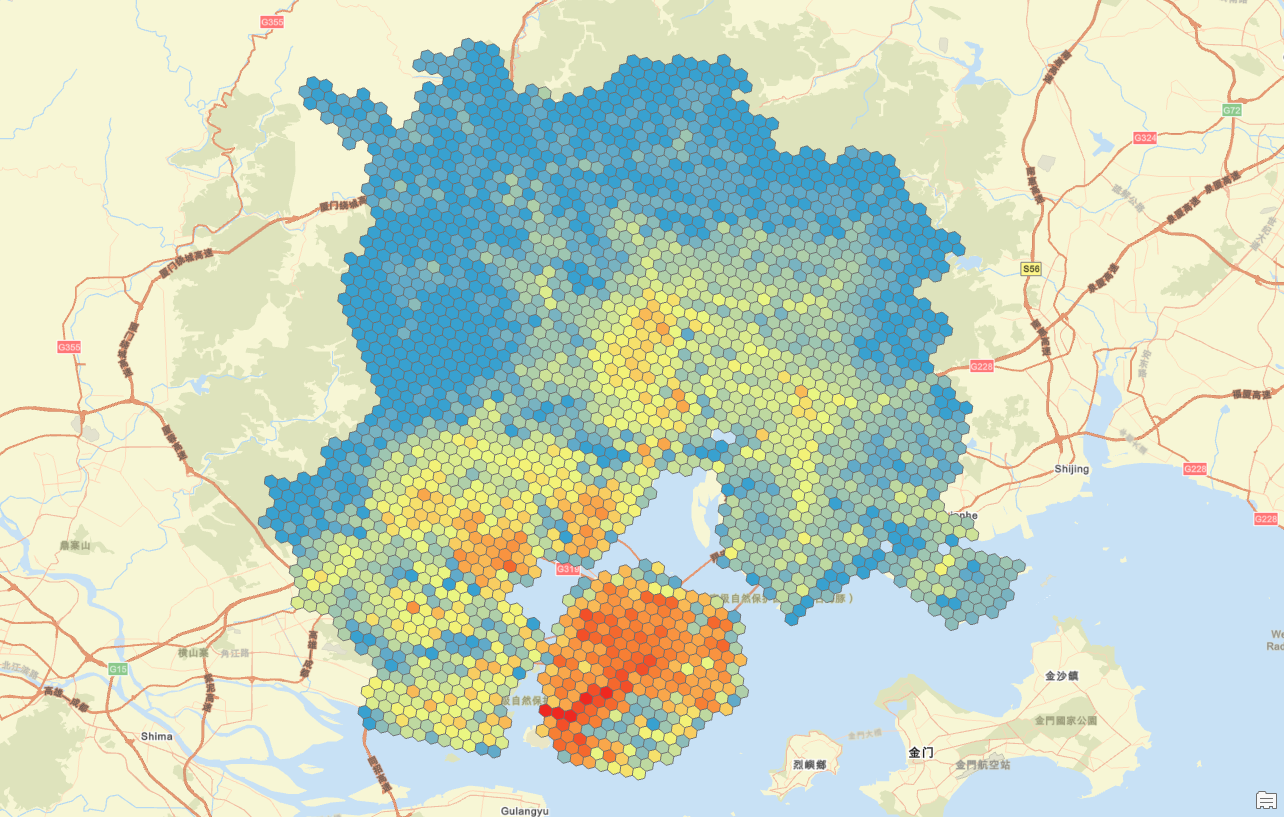
这是使用克里金插值法后的人口分布图,可以看到明显数据过度就好看很多;
文章仅用于分享个人学习成果与个人存档之用,分享知识,如有侵权,请联系作者进行删除。所有信息均基于作者的个人理解和经验,不代表任何官方立场或权威解读。
