【C++高阶四】红黑树

1.什么是红黑树

上篇博客学习了平衡二叉搜索树(AVLTree)，了解到AVL树的性质，二叉搜索树因为其独特的结构，查找、插入和删除在平均和最坏情况下时间复杂度都是O(logn)。
但在AVL树中插入或删除节点时，高度差绝对值大于1，平衡被破坏，为了重新维持其稳定，要进行旋转处理，但因为每个结点的高度差的绝对值都要小于1这个条件较为的严格，导致多数情况的插入和删除都需要旋转调整，导致插入和删除的效率降低
红黑树应运而生，并且因为其接近平衡的结构，使其查找效率十分高效，也没有像AVL树那样的严格要求，所以其插入和删除效率有时还优于AVL树

红黑树，是一种二叉搜索树，每个结点上增加一个存储位表示结点的颜色（红色或黑色），通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保最长路径不超过最短路径的二倍，因此接近平衡

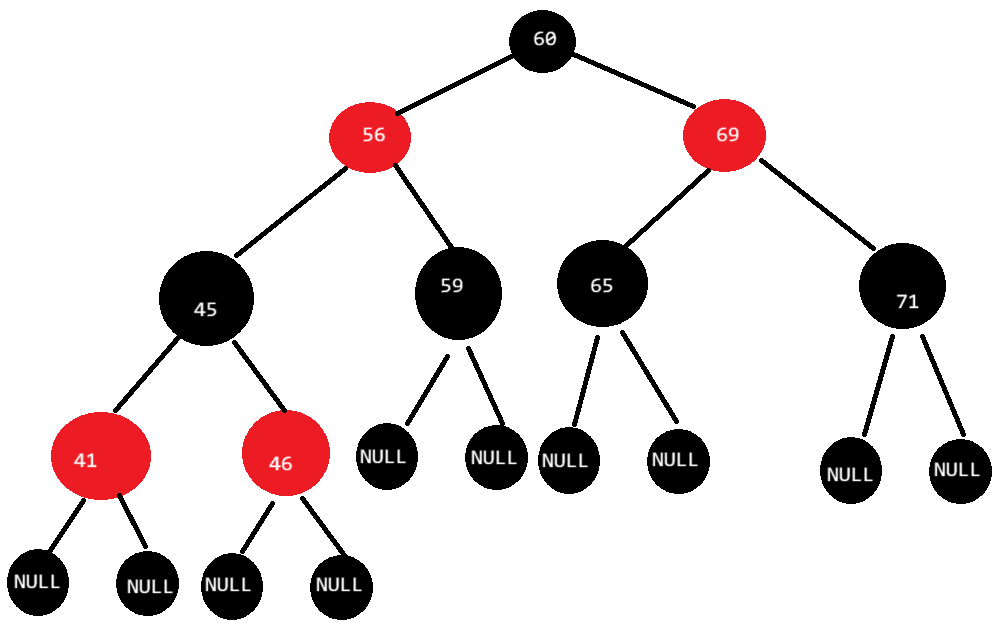
红黑树保持接近平衡是依靠以下几个规则：

1. 每个结点不是红色就是黑色
2. 根结点是黑色的
3. 如果一个结点是红色的，则它的两个孩子结点是黑色的
4. 对于每个结点，从该节点到其后代叶子结点的简单路径上，均包含相同数目的黑色结点
5. 每个叶子结点都是黑色的（此处的叶子结点指的是空结点）

由规则三可知：红黑树中没有连续的红色结点
由规则四可知：每一条路径都包含相同数目的黑色节点

2.红黑树的效率

红黑树的最短路径：全黑
红黑树的最长路径：一黑一红，红黑相间
假设总共有N个结点
那么最短路径就是以2为底的logN
最长路径就是2logN
而AVL树的查找效率是logN，和2logN差距并不大
但是红黑树的调整没有AVL树频繁，所以综合效率红黑树更胜一筹

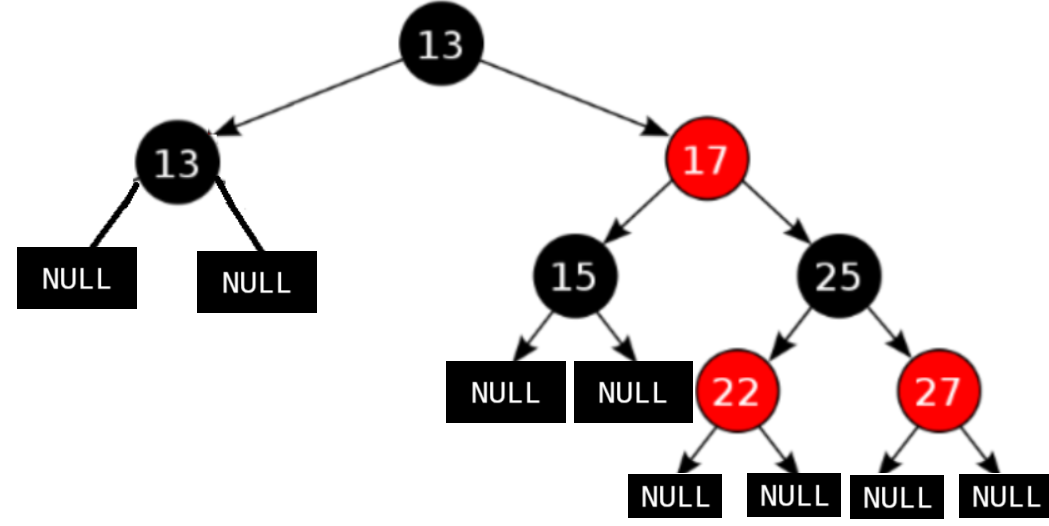
像这样一棵树，如果是AVL树，则右边高度比左边高2，需要旋转，但是符合红黑树的条件，不用旋转

3.红黑树的实现

3.1框架搭建

enum color//颜色枚举
{RED,BLACK,
};template<class K,class V>
struct RBTreeNode//节点结构体
{RBTreeNode<K, V>* _left;//左指针RBTreeNode<K, V>* _right;//右指针RBTreeNode<K, V>* _parent;//父亲指针color _color;//颜色标记位pair<K, V> _KV;//KV值RBTreeNode(const pair<K, V>& KV)//初始化列表构造:_left(nullptr), _right(nullptr), _parent(nullptr), _KV(KV), _color(RED){}
};template<class K,class V>
class RBTree
{typedef RBTreeNode<K, V> Node;//简称节点为Node
private:Node* _root = nullptr;
};

3.2 插入操作

和AVL树很相似，红黑树的插入也是分为两步：

1. 按照二叉搜索树的规则插入值
2. 插入后根据颜色或高度做旋转或变色

第一步可以将之前AVL的代码抄过来

bool insert(const pair<K, V>& kv)//按照二叉搜索树的方式插入值
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根节点是黑的return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first)//向右走{parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first)//向左走{parent = cur;cur = cur->_left;}else return false;//相等就插入失败}cur = new Node(kv);//链接if (parent->_kv.first < kv.first)parent->_right = cur;elseparent->_left = cur;//此时new出来的节点的parent还指向空cur->_parent = parent;
}

新插入的节点是选择插入红色还是黑色？有两个选择：

1. 插入黑色节点，打破规则四，要检查每个路径
2. 插入红色节点，打破规则三，只用看父亲是否为红

因此新插入的节点是选择成为红色是更优选择

3.2.1插入情况一

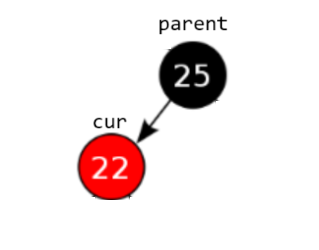
cur是新增红色结点，因为parent是黑色父节点，符合所有规则，插入完成

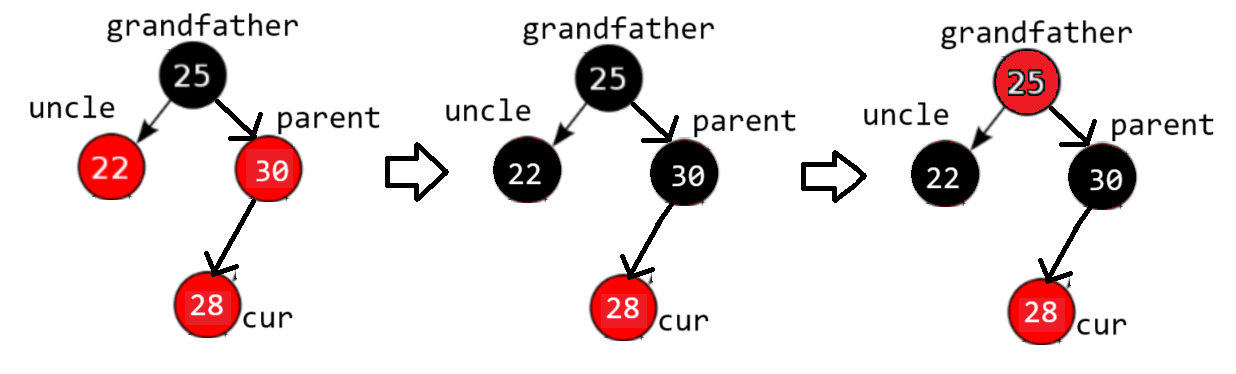
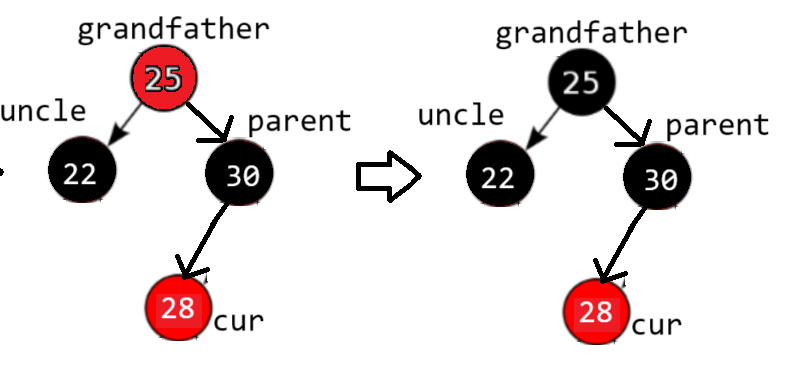
3.2.2插入情况二：uncle节点是红色的

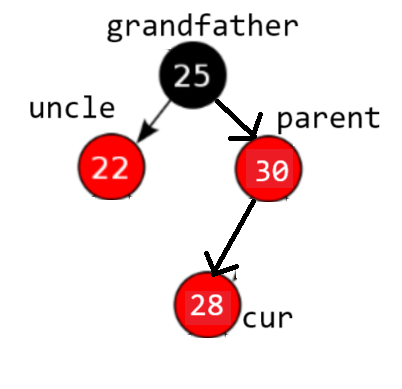
cur是新增红色结点28，因为parent是红色父节点30，插入28后导致连续的红色节点，违反规则三。
我们在处理时也要考虑规则四：每个路径的黑色结点的个数相同。
为了同时满足规则三和规则四，我们要改变结点颜色的同时，路径上的黑色结点个数还要相同：细致改变颜色向上更新，到达两个路径的公共节点，再改变公共结点的颜色

在情况二例子中的具体操作：当存在红色的uncle节点时，将uncle和parent节点的颜色都变为黑色，再将grandfather节点变为红色

如果grandfather是根节点，再将grandfather结点变成黑色

如果grandfather不是根节点且红黑树的节点数量更多呢？

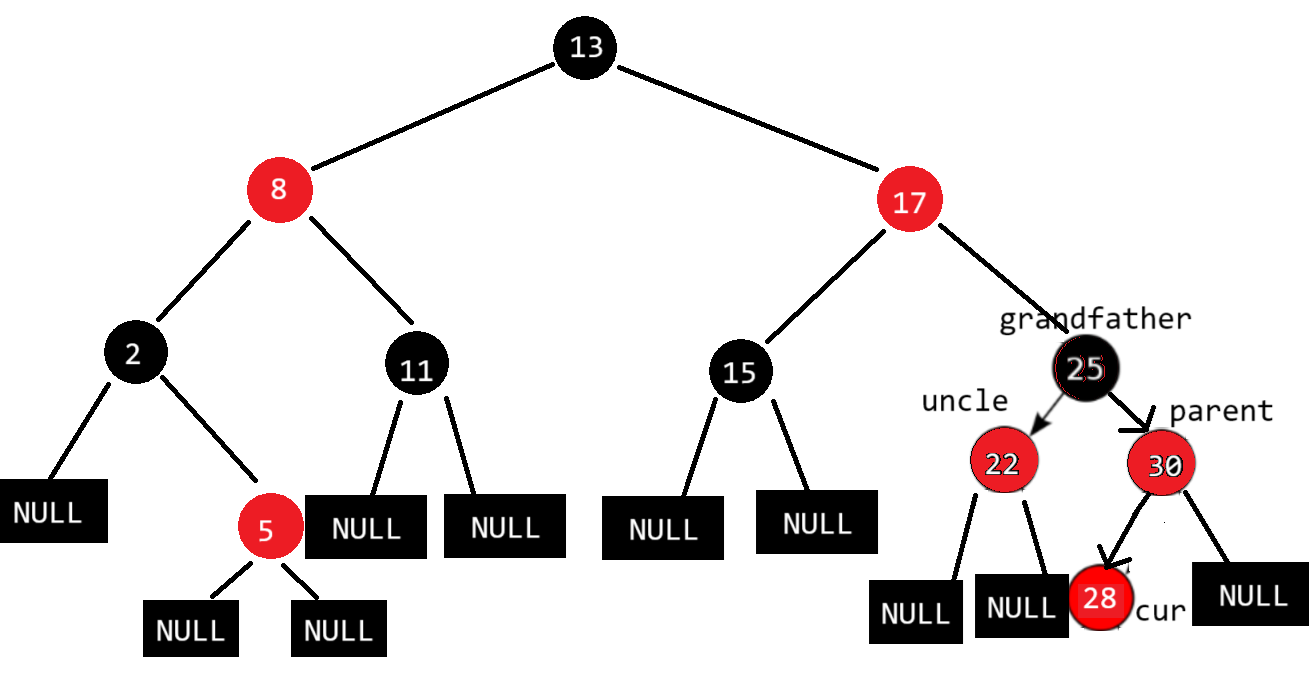
28为新增红色节点，同样使用上述方法调节颜色

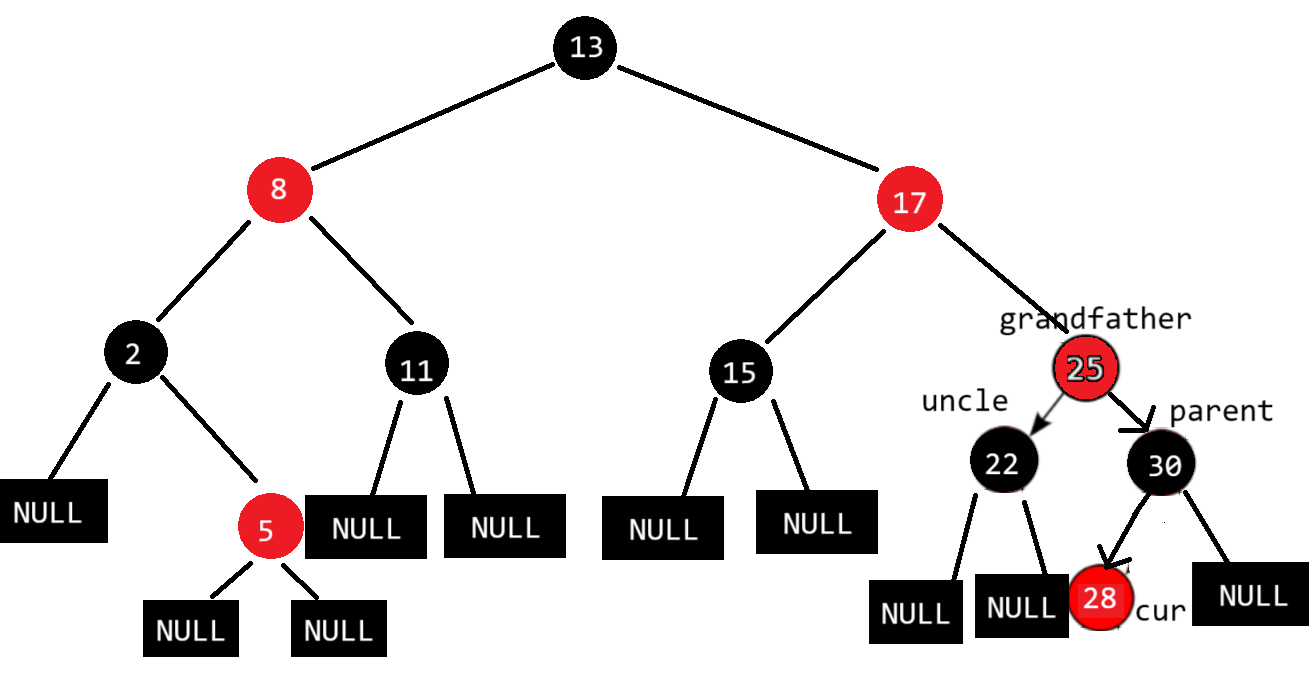
以25为根结点的子树完成了调整，但这只是完成了一颗子树，所以还需要继续向上调整

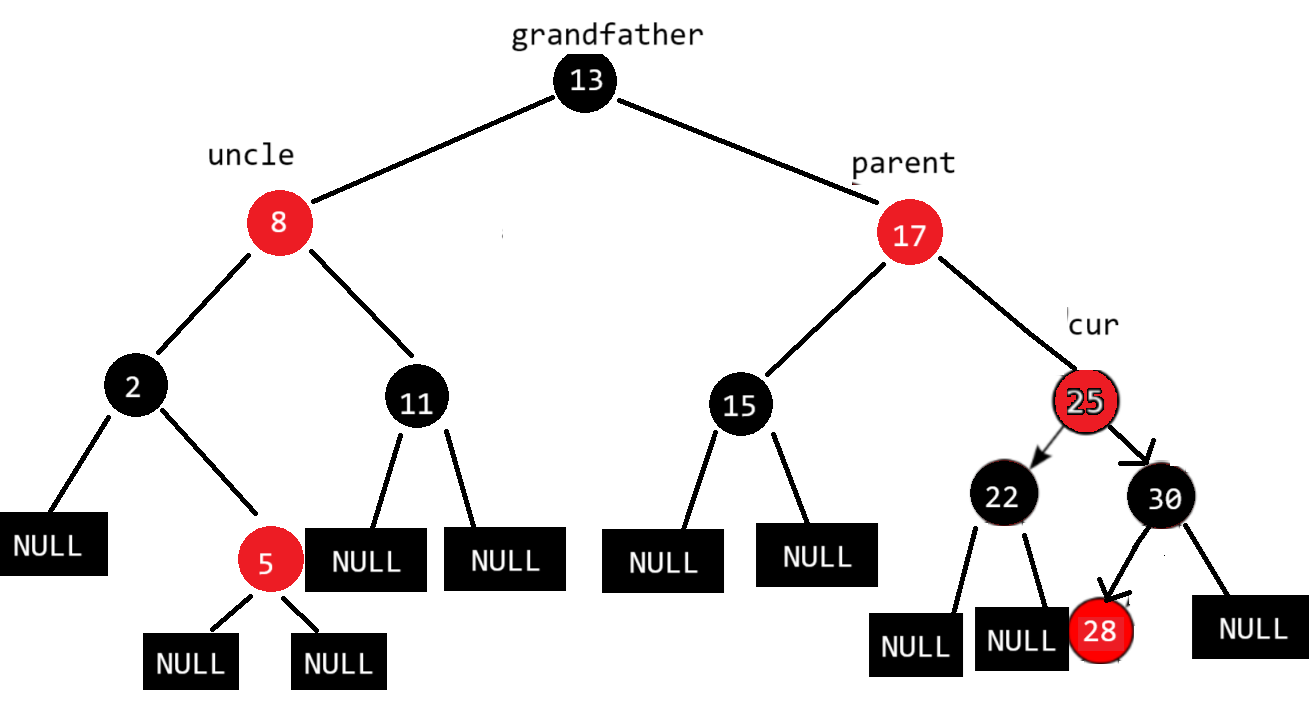
这时新的parent有两种情况：

1. parent结点为黑色，调整结束
2. parent结点为红色，继续调整

此处parent结点是红色，所以我们还需继续调整

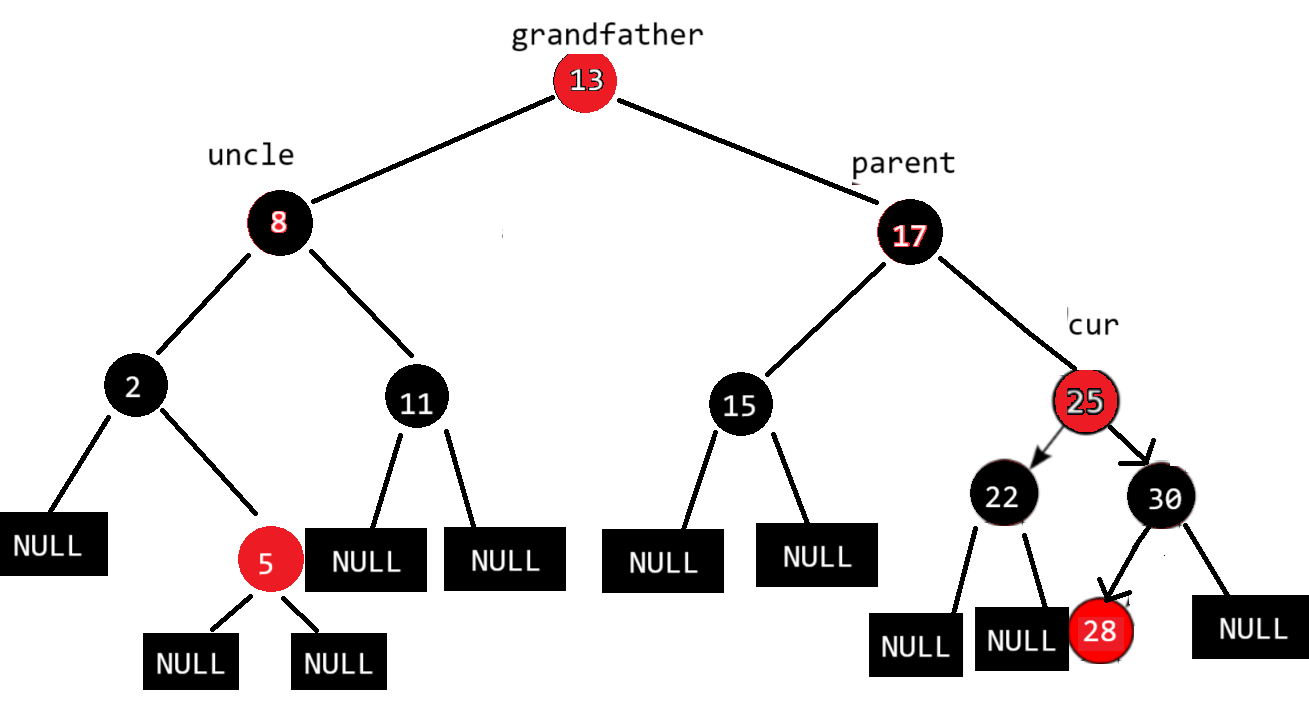
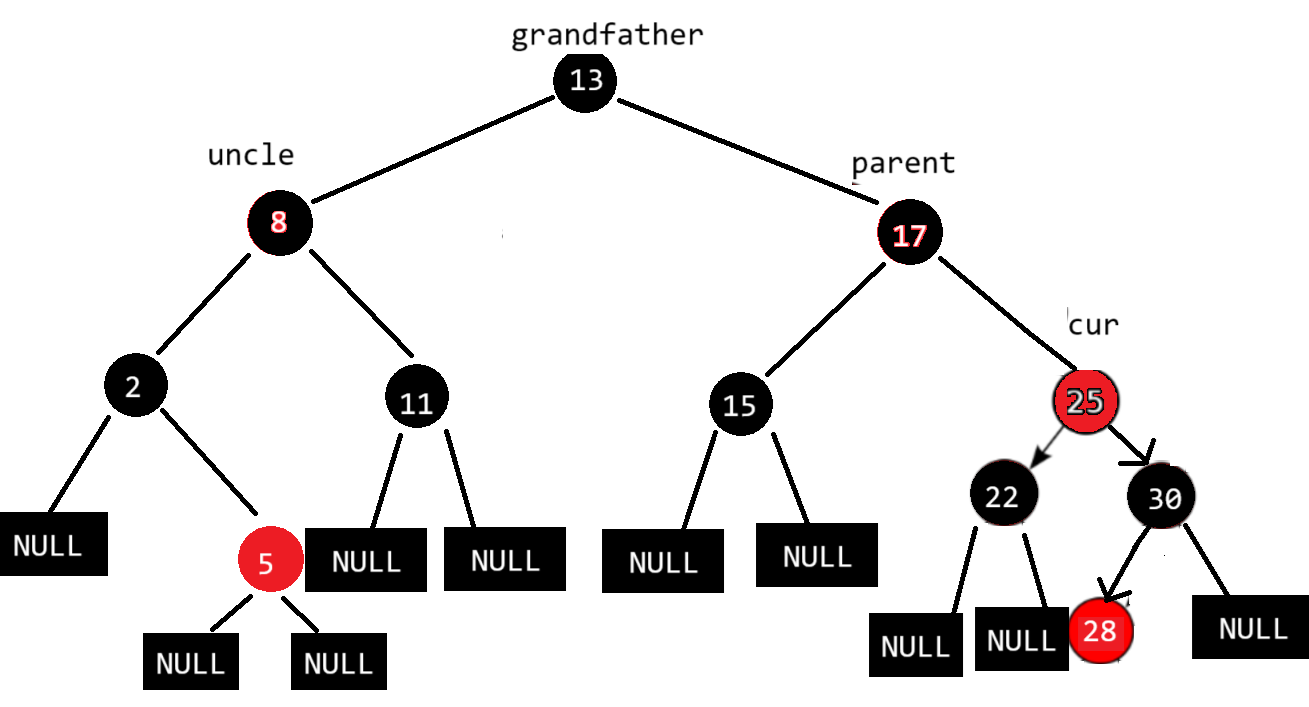
这就是情况二：新插入结点的父亲结点是红色的，uncle结点存在且为红的情况下，将parent和uncle都变黑，grandfather变红，若grandfather不为根还需要继续向上更新，若grandfather为根就将其变成黑色

3.2.3插入情况三：没有uncle结点

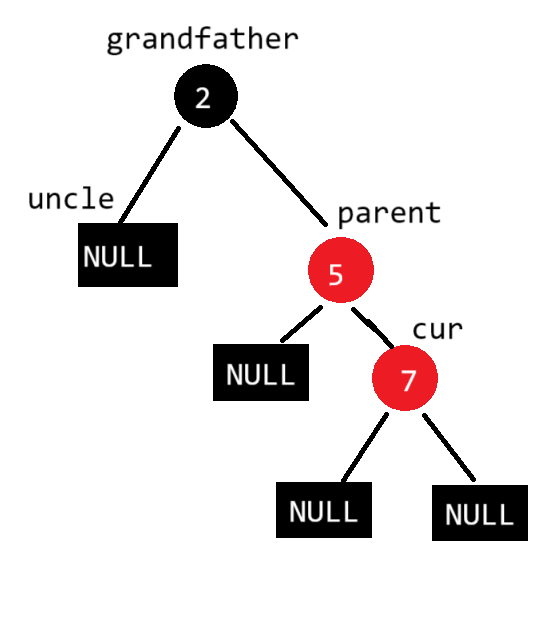
在5的右边新增结点，此时没有uncle结点，不是情况二
通过观察发现，这棵树的高度很不均衡，我们可以采用旋转的方式降低这棵树的高度
使用左单旋：

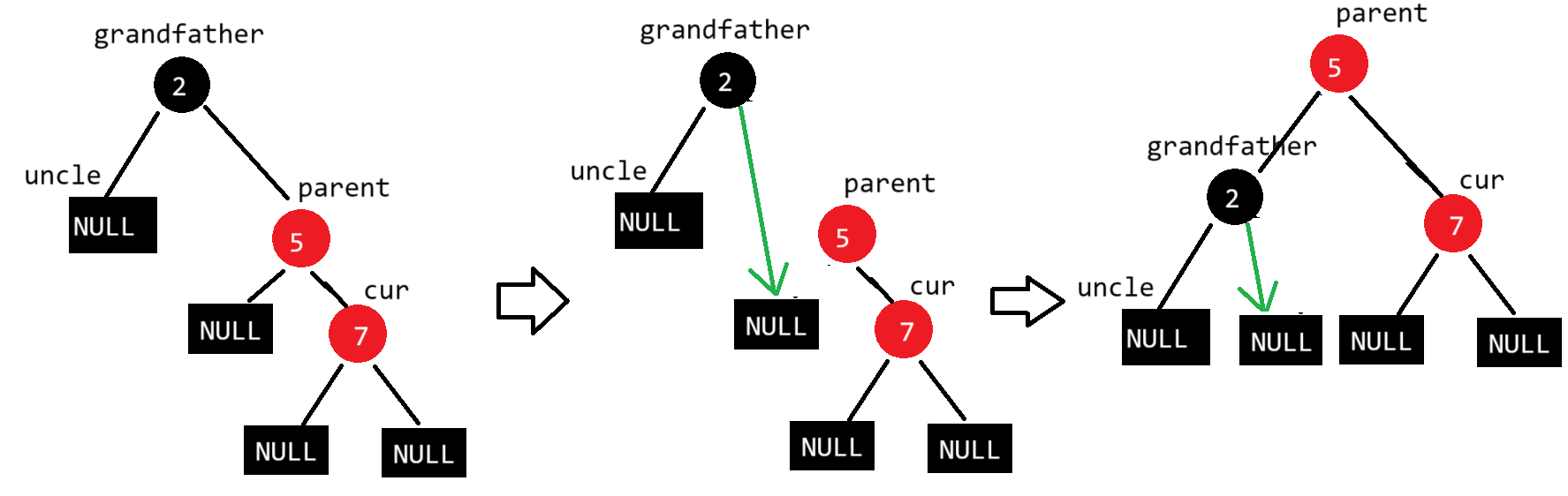
没有破坏二叉搜索树的结构的情况下降低了树的高度，但仍然不满足红黑树，继续调整颜色：将grandfather变红，parent变黑

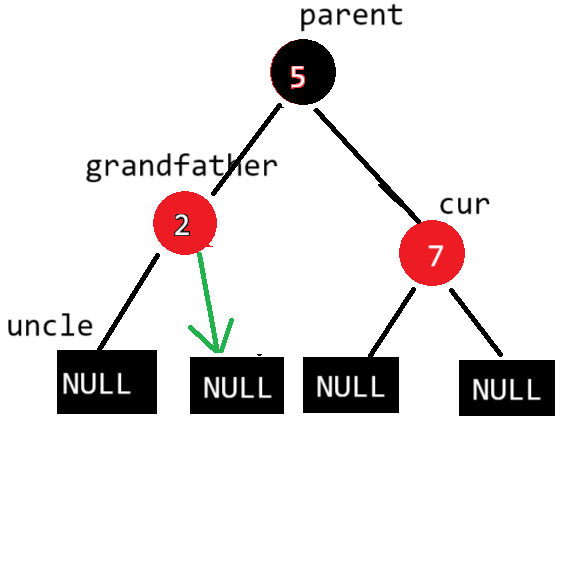
当情况三出现在子树部分也可以完美符合规则

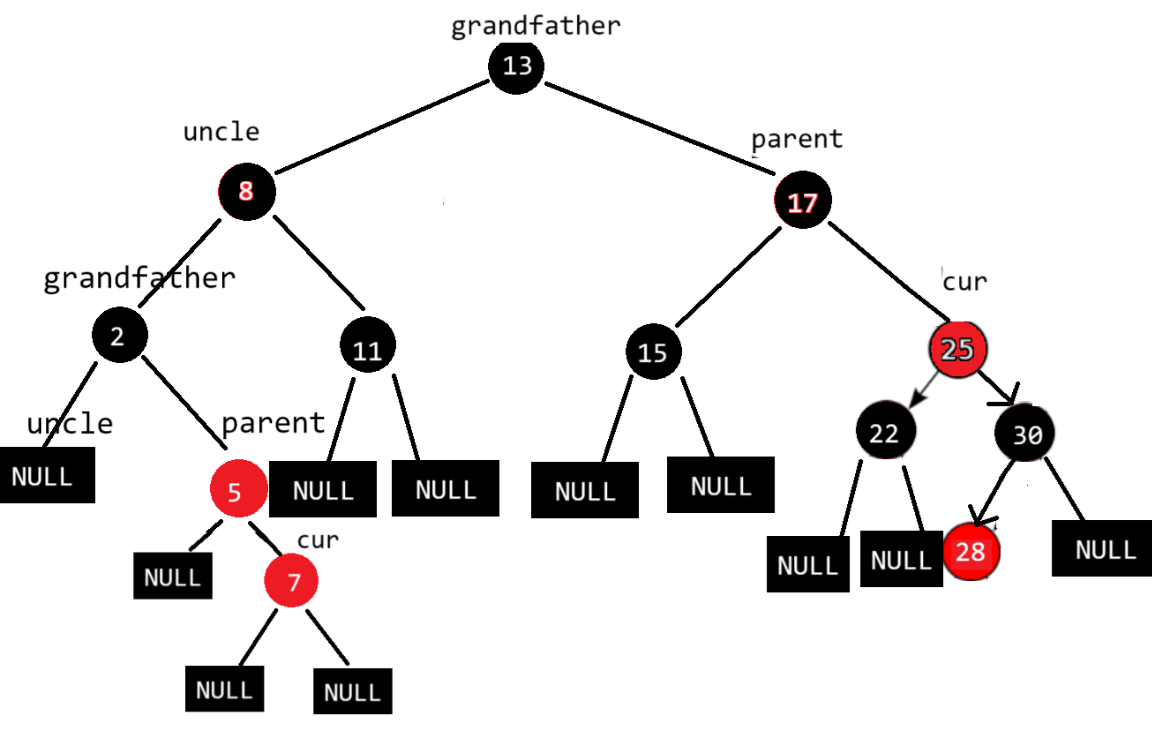
旋转变色后：整棵树也符合规则

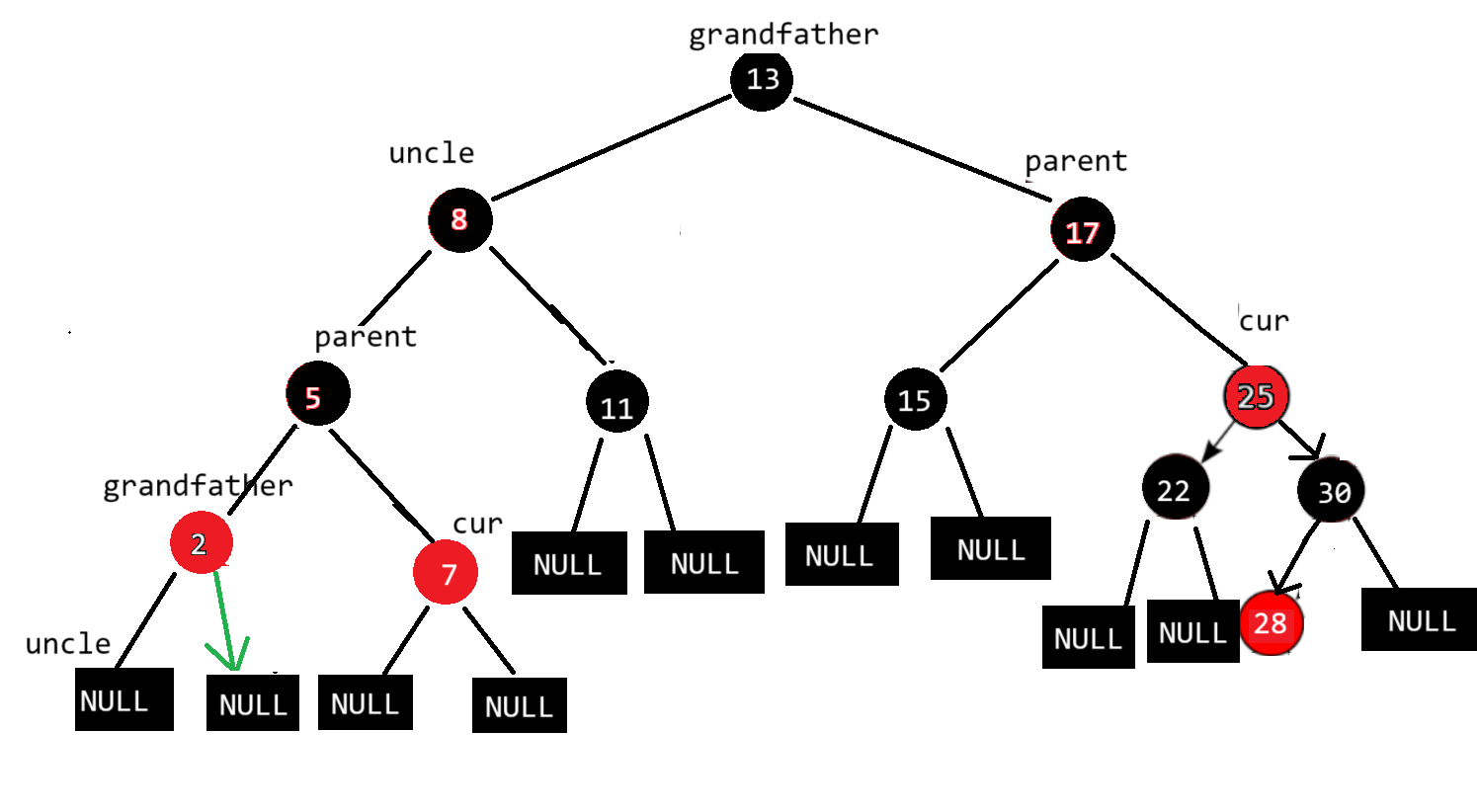
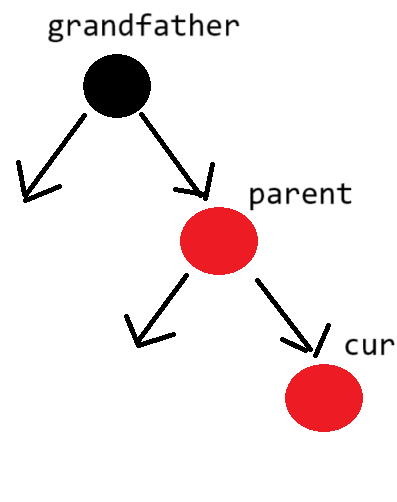
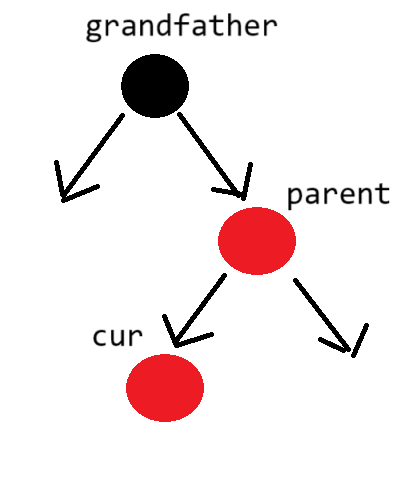
当grandfather、parent和cur线性排列时使用单旋

当grandfather、parent和cur折线排列时使用双旋

3.2.4插入情况四：uncle节点是黑色的

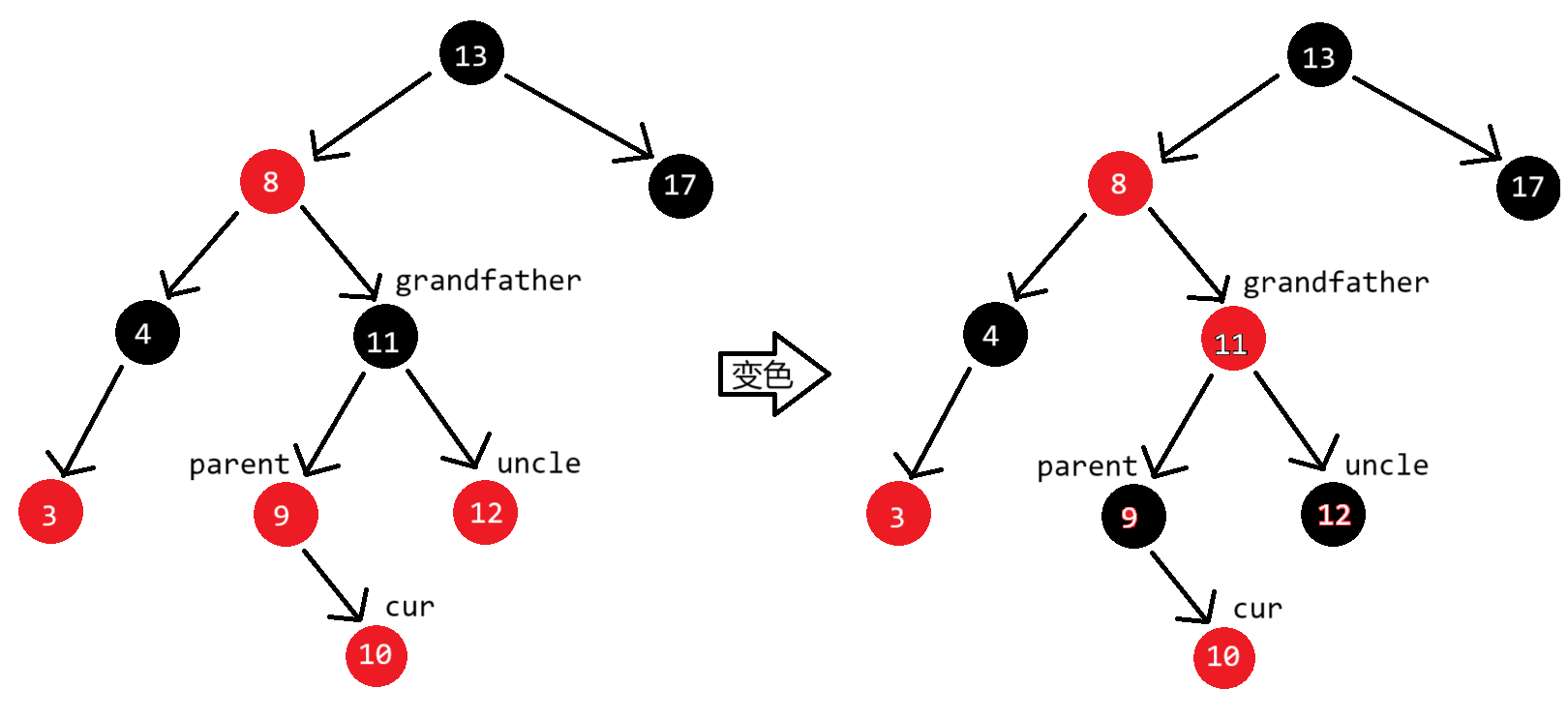
插入19红色节点并调整颜色后，继续向上调整：

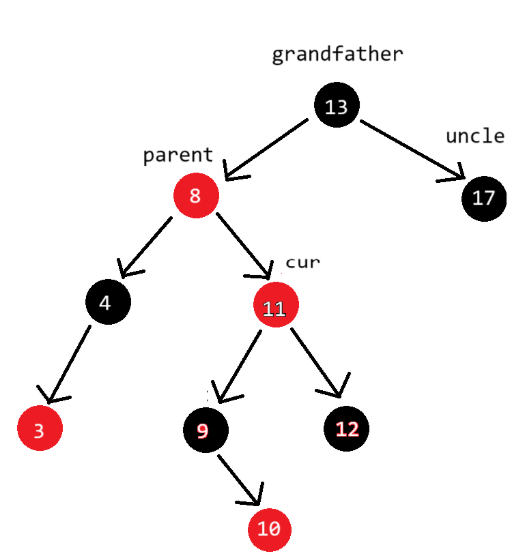
parent是红色，但是uncle却是黑色
因为grandfather、parent和cur呈折线排列，所以使用双旋
左右双旋：先左单旋，后右单旋

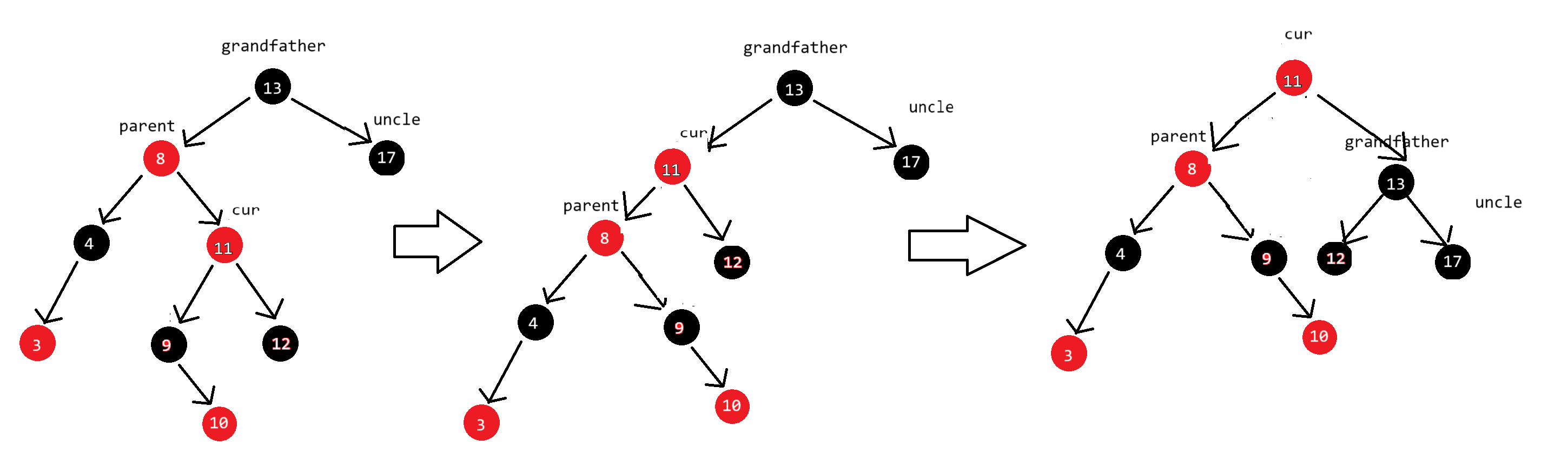
旋转结束后调整颜色：cur变成黑色，grandfather变成红色

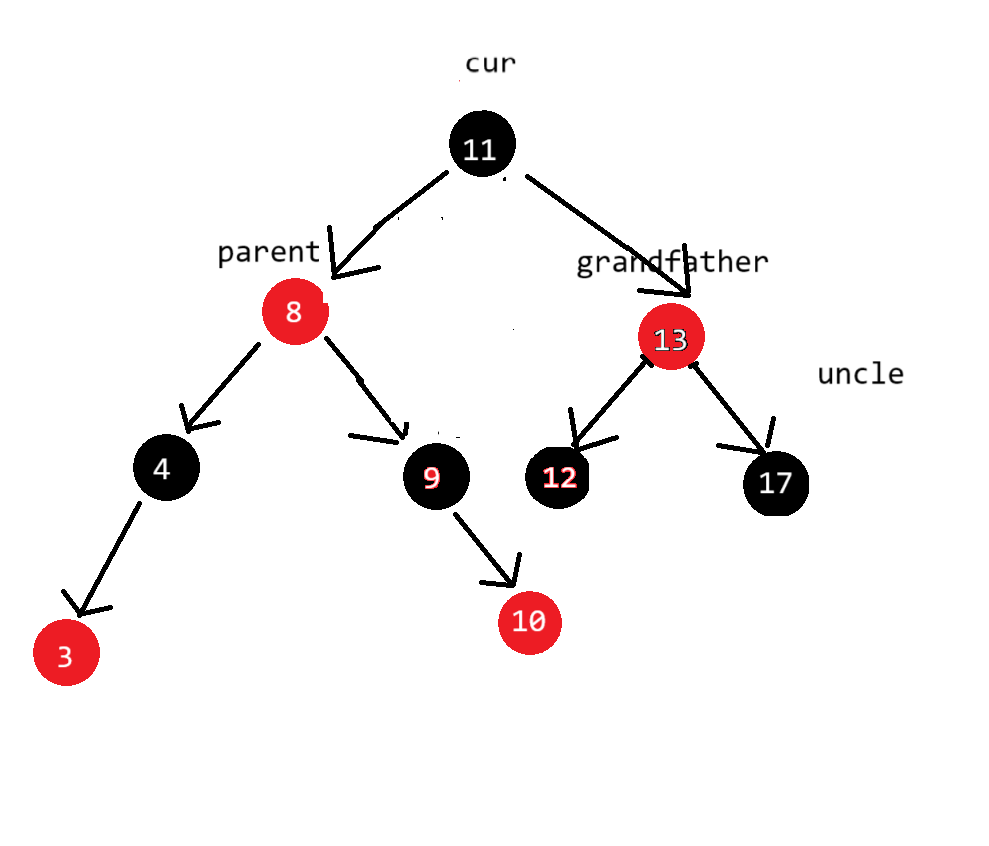
无论哪种情况的旋转，看是线性还是折线，线性使用单旋，折线型使用双旋

4.完整代码

#pragma once
#include <iostream>
#include <assert.h>using namespace std;enum color//颜色枚举
{RED,BLACK
};template<class K,class V>
struct RBTreeNode//节点结构体
{RBTreeNode<K, V>* _left;//左指针RBTreeNode<K, V>* _right;//右指针RBTreeNode<K, V>* _parent;//父亲指针color _color;//颜色标记位pair<K, V> _kv;//KV值RBTreeNode(const pair<K, V>& KV)//初始化列表构造:_left(nullptr), _right(nullptr), _parent(nullptr), _kv(KV), _color(RED){}
};template<class K,class V>
class RBTree
{typedef RBTreeNode<K, V> Node;//定义节点为Node
public:bool Insert(const pair<k, v>& kv){if (_root == nullptr){_root = new Node(kv);_root->_color = BLACK;//根节点是黑的return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first)//向右走{parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first)//向左走{parent = cur;cur = cur->_left;}else{return false;//相等就插入失败}}cur = new Node(kv);//链接if (parent->_kv.first < kv.first)parent->_right = cur;elseparent->_left = cur;//此时new出来的节点的parent还指向空cur->_parent = parent;//新插入节点的父亲 存在 且是 红色,再调整while (parent && parent->_color == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left)//新插入的节点其父节点在子树左侧{Node* uncle = grandfather->_right;if (uncle && uncle->_color == RED)//uncle存在且为红{uncle->_color = parent->_color = BLACK;grandfather->color = RED;cur = grandfather;parent = cur->_parent;}else//uncle不存在 或uncle是黑色{if (cur = parent->left)//grandfather和parent和cur是线性{RotateR(grandfather);grandfather->color = RED;parent->color = BLACK;}else//grandfather和parent和cur是折线型{RotateL(parent);RotateR(grandfather);cur->color = BLACK;grandfather->_color = RED;}break;//旋转后一定满足要求，跳出循环}}else//新插入的节点其父节点在子树右侧{Node* uncle = grandfather->_left;if (uncle && uncle->_color == RED)//uncle 存在 且为 红色{uncle->_color = parent->_color = BLACK;grandfather->color = RED;cur = grandfather;parent = cur->_parent;}else//uncle 不存在 或为 黑色{if (cur = parent->right)//grandfather和parent和cur是线性{RotateL(grandfather);grandfather->color = RED;parent->color = BLACK;}else//grandfather和parent和cur是折线型{RotateR(parent);RotateL(grandfather);cur->color = BLACK;grandfather->_color = RED;}break;//旋转后一定满足要求，跳出循环}}}_root->color = BLACK;return true;}void RotateL(Node* parent)//左单旋{Node* subR = parent->_right;Node* subRL = subR->_ + left;parent->_right = subRL;if (subRL){subRL->_parent = parent;}Node* parentparent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (parentparent->_left = parent){parentparent->_left = subR;}else{parentparent->_right = subR;}subR->_parent = parentparent;}subR->_bf = parent->_bf = 0;}void RotateR(Node* parent)//右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent)ppNode->_left = subL;elseppNode->_right = subL;subL->_parent = ppNode;}subL->_bf = parent->_bf = 0;}size_t size(){return _size(_root);}size_t _size(Node* root){if (root == nullptr)return 0;return _size(root->left) + _size(root->right) + 1;}Node* find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if(cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}void InOrder()//中序{_InOrder(_root);}int Height(){return _Height(_root);}
private:void _InOrder(Node* root)//中序{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}int _Height(Node* root){if (root == nullptr){return 0;}return max(_Height(root->left), _Height(root->right) + 1);}Node* _root = nullptr;
};