《通信原理》学习笔记——第二章
目录
确知信号
1.确知信号的类型
2.确知信号的频域性质
1.功率信号的频谱
2. 能量信号的频谱密度
3.能量信号的能量谱密度
4.功率信号的功率谱密度
3.确知信号的时域性质
1.能量信号的自相关函数
2.功率信号的自相关函数
3.能量信号的互相关函数
4.功率信号的互相关函数
确知信号
1.确知信号的类型
确知信号是指其取值在任何时间都是确定的和可预知的信号,通常可以用数学公式表示它在任何时间的取值
按照是否具有周期重复性,确知信号可以分为周期信号 (periodic signal) 和非周期信号 (nonperiodic signal)
在数学上,若信号 s(t) 满足下述条件:
![]()
式中 T0>0 ,为一常数,则称此信号为周期信号,否则为非周期信号,并将满足式 (2.1-1) 的最小 T0 称为此信号的周期,将 1/T0 称为基频 f0
按照能量是否有限区分,信号可以分为能量信号 (energy signal) 和功率信号 (power signal) 两类。在通信理论中,通常把信号功率定义为电流在单位电阻 (1Ω) 上消耗的功率,即归一化 (normalized) 功率 P 。因此,功率就等于电流或电压的平方:
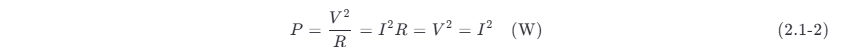
式中:V 为电压 (V);I 为电流 (A)。
可以认为,信号电流 I 或电压 V 的平方都等于功率。后面一般化为用 S 代表信号的电流或电压来计算信号功率。若信号电压和电流的值随时间变化,则 S 可以改写为时间 t 的函数 s(t) 。这时,信号能量 E 应当是信号瞬时功率的积分:
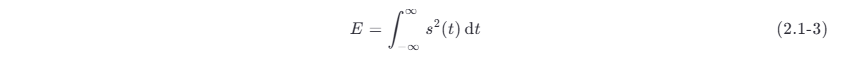
其中,E 的单位是焦耳 (J)。
若信号的能量是一个正的有限值,即
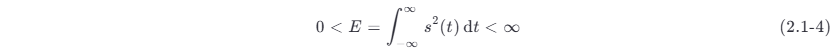
则称此信号为能量信号。
将信号的平均功率定义为
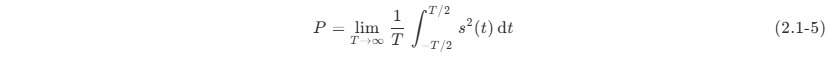
由式 (2.1-5) 看出,能量信号的平均功率 P=0 ,因为式 (2.1-5) 表示若信号的能量有限,则在被趋于无穷大的时间 T 去除后,所得平均功率趋近于零。
实际的通信系统中,信号都具有有限的功率、有限的持续时间,因而具有有限的能量。但是,若信号的持续时间非常长,如广播信号,则可以近似认为它具有无限长的持续时间。此时,认为由式 (2.1-5) 定义的信号平均功率是一个有限的正值,但是其能量近似等于无穷大。我们把这种信号称为功率信号
信号可以分成两类:
① 能量信号,其能量等于一个有限正值,但平均功率为零;
② 功率信号,其平均功率等于一个有限正值,但能量为无穷大。
顺便提醒,能量信号和功率信号的分类对于非确知信号也适用
2.确知信号的频域性质
信号的频率特性有 4 种,即功率信号的频谱、能量信号的频谱密度、能量信号的能量谱密度和功率信号的功率谱密度
1.功率信号的频谱
对于周期性的功率信号,很容易计算其频谱。设一个周期性功率信号 s(t) 的周期为 T0 ,则将其频谱 (frequency spectrum) 函数定义为下式积分:
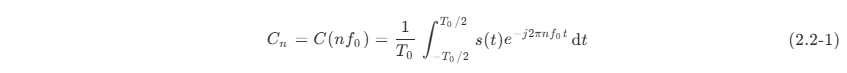
式中:f0=1/T0 ;n 为整数,−∞<n<+∞ ;C(nf0) 表示 C 是 nf0 的函数,并简记为 Cn 。
由傅里叶级数 (Fourier series) 理论可知,式 (2.2-1) 就是周期性函数展开成傅里叶级数的系数,即周期性信号可以展开成如下的傅里叶级数:
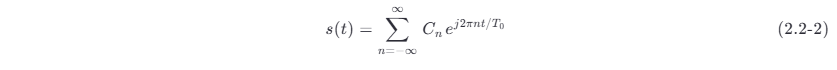
在数学上能将周期性函数展开成傅里叶级数的狄利克雷 (Dirichlet) 条件,一般信号都是能满足的。
当 n=0 时,式 (2.2-1) 变成
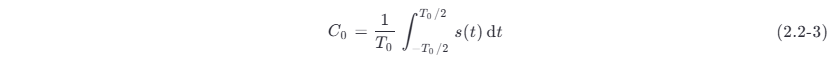
它是信号 s(t) 的时间平均值,即直流分量。
一般说来,式 (2.2-1) 中频谱函数 Cn 是一个复数,代表在频率 nf0 上信号分量的复振幅 (complex amplitude)。可以把它写作
![]()
式中:∣Cn∣ 为频率 nf0 的信号分量的振幅;θn 为频率 nf0 的信号分量的相位。
式 (2.2-4) 表示,对于周期性功率信号来说,其频谱函数 Cn 是离散的,只在 f0 的整数倍上取值。由于 n 可以取负值,所以在负频率上 Cn 也有值。通常称 Cn 为双边 (频) 谱。双边谱仅在数学上有意义;在物理上,并不存在负频率。但是可以找到物理上实信号的频谱和数学上的频谱函数之间的关系
对于物理可实现的实信号,由式 (2.2-1) 有
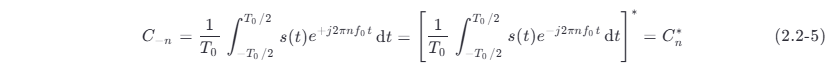
即频谱函数的正频率部分和负频率部分间存在复数共轭关系。这就是说,负频谱和正频谱的模是偶对称的,相位是奇对称的,如图所示。
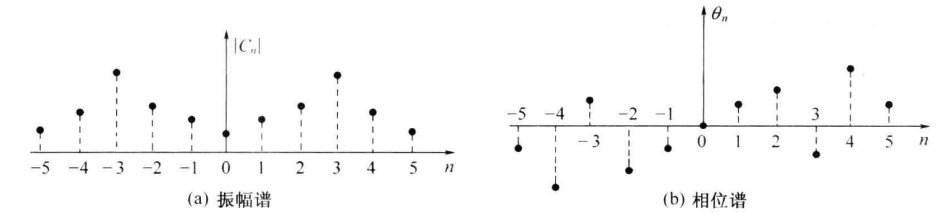
将式 (2.2-5) 代入式 (2.2-2),并利用欧拉公式,得到
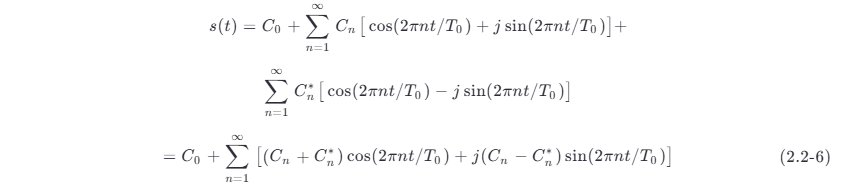
令
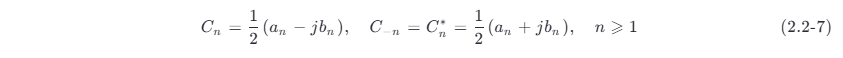
将式 (2.2-7) 关系代入式 (2.2-6),有
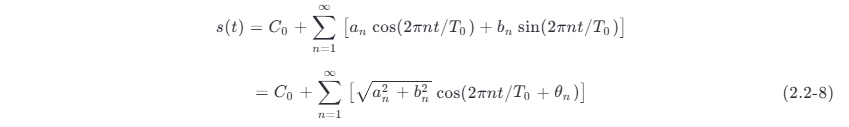
式中
![]()
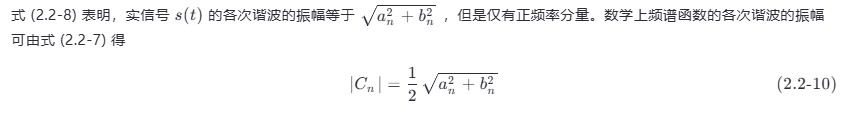

由式 (2.2-11) 可见,若 s(t) 是偶信号,则因被积函数是奇函数,使 Cn 的虚部等于 0,即
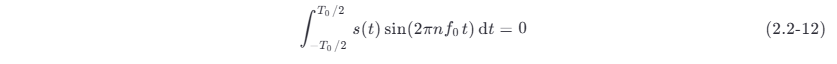
所以 Cn 为实函数。
2. 能量信号的频谱密度
设一个能量信号为 s(t) ,则将它的傅里叶变换 S(f) 定义为它的频谱密度 (frequency spectrum density)
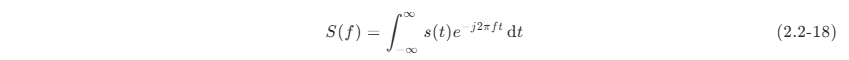
而 S(f) 的逆傅里叶变换就是原信号:
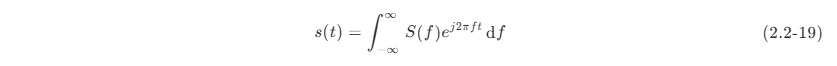
能量信号的频谱密度 S(f) 和周期性功率信号的频谱 Cn 的主要区别有两点:第一,S(f) 是连续谱,Cn 是离散谱;第二,S(f) 的单位是伏/赫 (V/Hz),而 Cn 的单位是伏 (V)。能量信号的能量有限,并分布在连续频率轴上,所以在每个频率点 f 上信号的幅度是无穷小;只有在一小段频率间隔 df 上才有确定的非零振幅。功率信号的功率有限,但能量无限,它在无限多的离散频率点上有确定的非零振幅。顺便指出,在后面章节,在针对能量信号讨论问题时,也常把频谱密度简称为频谱;这时在概念上不要把它和周期信号的频谱相混淆。
实能量信号的频谱密度和实功率信号的频谱有一个共同的特性,即其负频谱和正频谱的模偶对称。这可以从式 (2.2-20) 看出:
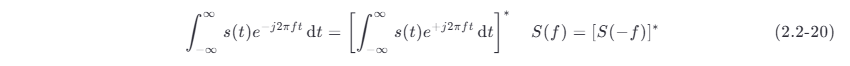
或者说,其频谱密度的正频率部分和负频率部分成复数共轭 (complex conjugate)关系。
3.能量信号的能量谱密度
设一个能量信号 s(t) 的能量为 E ,则此信号的能量为
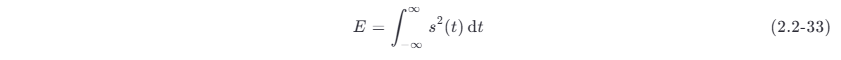
若此信号的傅里叶变换(频谱密度)为 S(f) ,则由巴塞伐尔 (Parseval) 定理得知
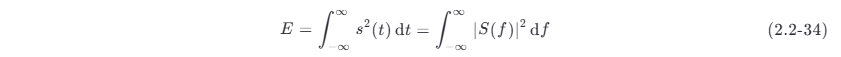
式 (2.2-34) 表示 ∣S(f)∣^2 在频率轴 f 上的积分等于信号能量,所以称 ∣S(f)∣^2 为能量谱密度 (energy spectrum density),它表示在频率 f 处宽度为 df 的频带内的信号能量,或者也可以看作是单位频带内的信号能量。式 (2.2-34) 可以改写为
![]()
式中
![]()
为能量谱密度
由于信号 s(t) 是一个实函数,所以 ∣S(f)∣ 是一个偶函数。因此,式 (2.2-35) 可以写为
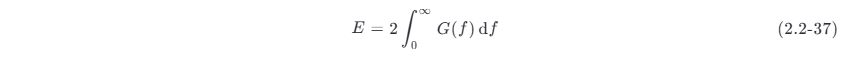
4.功率信号的功率谱密度
由于功率信号具有无穷大的能量,式 (2.2-33) 的积分不存在,所以不能计算功率信号的能量谱密度。但是,可以求出它的功率谱密度。为此,首先将信号 s(t) 截短为长度等于 T 的一个截短信号 sT(t) ,−T/2<t<T/2 。这样,sT(t) 就成为一个能量信号了。对于这个能量信号,就可以用傅里叶变换求出其能量谱密度 ∣ST(f)∣2 ,并由巴塞伐尔定理有
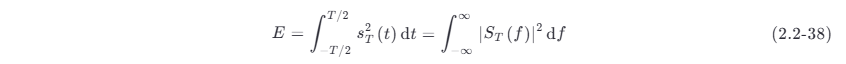
于是,可以将
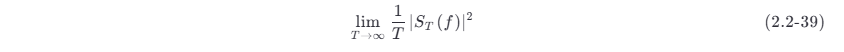
定义为信号的功率谱密度 (power spectrum density) P(f) ,即
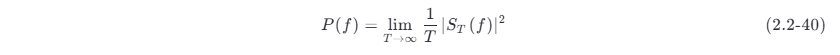
信号功率则为
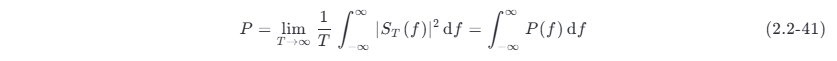
若此功率信号具有周期性,则可以将 T 选作等于信号的周期 T0 ,并且用傅里叶级数代替傅里叶变换,求出信号的频谱。这时,式 (2.1-5) 变成
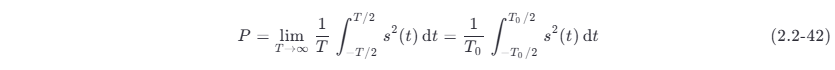
并且由周期函数的巴塞伐尔定理得知
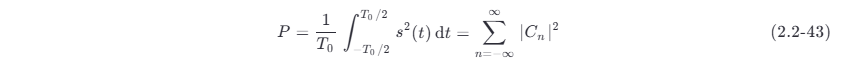
式中:Cn 为此周期信号的傅里叶级数的系数。
若 f0 是此信号的基波频率,则 Cn 是此信号的第 n 次谐波(其频率为 nf0 )的振幅;∣Cn∣2 为第 n 次谐波的功率,可以称为信号的(离散)功率谱。
若仍希望用连续的功率谱密度表示此离散谱(discrete spectrum),则可以利用上述的 δ 函数的特性(式 (2.2-27))将式 (2.2-43) 表示为
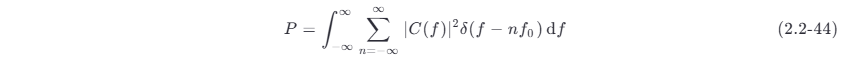
式中
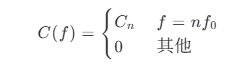
式 (2.2-44) 中的被积因子就是此信号的功率谱密度 P(f) ,即
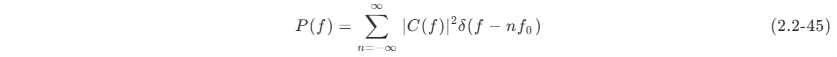
而
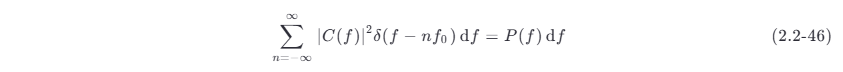
就是在频率间隔 df 内信号的功率。
3.确知信号的时域性质
确知信号在时域中的性质主要有自相关函数和互相关函数
1.能量信号的自相关函数
能量信号 s(t) 的自相关函数的定义为
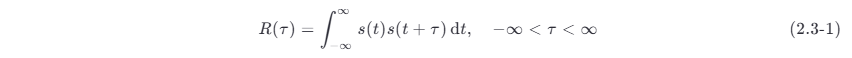
自相关函数反映了同一个信号与延迟 τ 后的同一信号间的相关程度。自相关函数 R(τ) 和时间 t 无关,只和时间差 τ 有关。当 τ=0 时,能量信号的自相关函数 R(0) 等于信号的能量,即
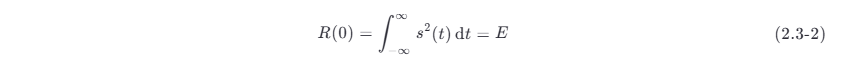
式中:E 为能量信号的能量。
此外,R(τ) 是 τ 的偶函数,即
![]()
能量信号的自相关函数和其能量谱密度之间有简单的关系。下面具体分析。对定义式 (2.3-1) 求傅里叶变换,即
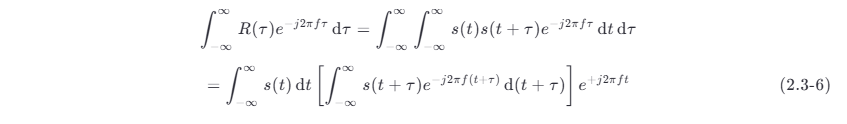
令 t′=t+τ 代入式 (2.3-6),得

因为一般说来 S(f) 是复函数,所以可以令
![]()
式中:A(f) 和 B(f) 为实函数。并且,对于实能量信号,其频谱密度的正频率部分和负频率部分有复数共轭关系。这样,式 (2.3-7) 变为
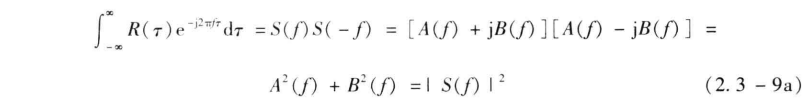
将式 (2.3-9a) 和式 (2.2-34) 比较表明,能量信号的自相关函数的傅里叶变换就是其能量谱密度。反之,能量信号的能量谱密度的逆傅里叶变换就是能量信号的自相关函数,即
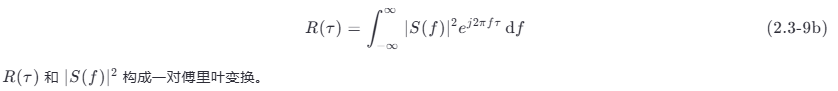
2.功率信号的自相关函数
功率信号 s(t) 的自相关函数的定义为
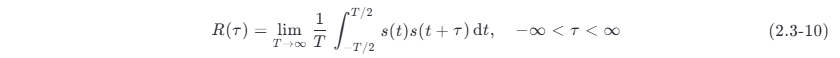
由定义式不难看出,当 τ=0 时,功率信号的自相关函数 R(0) 等于信号的平均功率,即
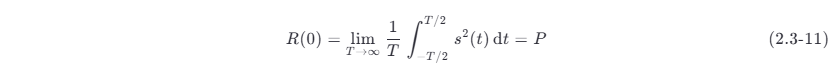
式中:P 为信号的功率
和能量信号的自相关函数类似,功率信号的自相关函数也是偶函数。
对于周期性功率信号,自相关函数的定义可以改写为
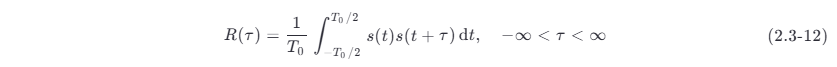
周期性功率信号的自相关函数和其功率谱密度之间也有简单的关系。下面具体分析。由式 (2.3-12),有
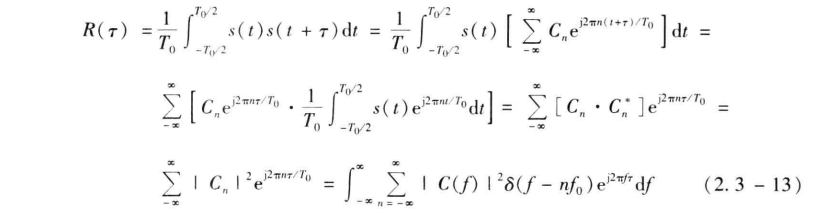
将式 (2.2-45) 代入式 (2.3-13),得
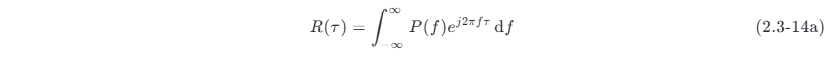
式 (2.3-14a) 表明,周期性功率信号的自相关函数 R(τ) 和其功率谱密度 P(f) 之间是傅里叶变换关系,即 P(f) 的逆傅里叶变换是 R(τ) ,而 R(τ) 的傅里叶变换是功率谱密度,即
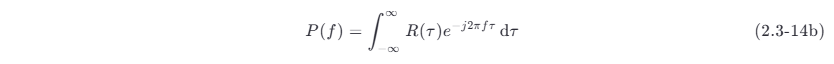
3.能量信号的互相关函数
两个能量信号 s1(t) 和 s2(t) 的互相关函数的定义为
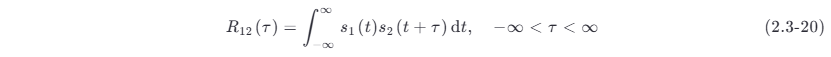
由式 (2.3-20) 看出,互相关函数反映了两个信号和延迟 τ 后的另一个信号间的相关程度。互相关函数 R12(τ) 和时间 t 无关,只和时间差 τ 有关。需要注意的是,互相关函数和两个信号相乘的前后次序有关,即有
![]()
考虑互相关函数和信号能量谱密度的关系。由定义式 (2.3-20),有
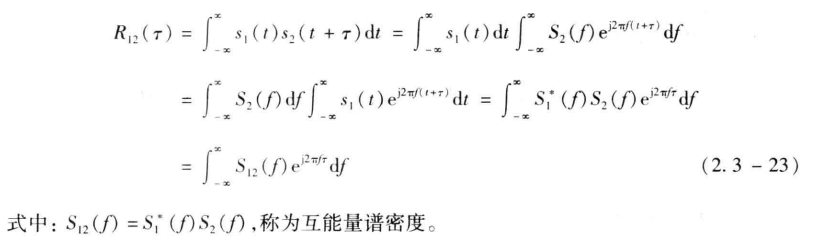
式 (2.3-23) 表示,R12(τ) 是 S12(f) 的逆傅里叶变换。故 S12(f) 是 R12(τ) 的傅里叶变换,即
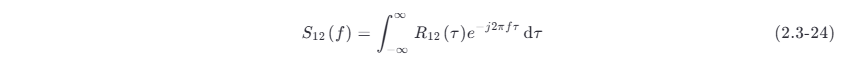
因此,互相关函数和互能量谱密度也是一对傅里叶变换。
4.功率信号的互相关函数
两个功率信号 s1(t) 和 s2(t) 的互相关函数的定义为
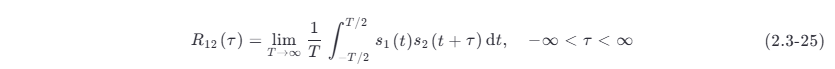
同样,功率信号的互相关函数 R12(τ) 也和时间 t 无关,只和时间差 τ 有关,并且互相关函数和两个信号相乘的前后次序有关。
若两个周期性功率信号的周期相同,则其互相关函数的定义可以写为
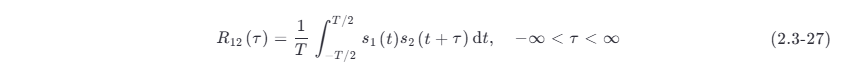
式中:T 为信号的周期
在功率信号的互相关函数和其功率谱之间也有如下的简单傅里叶变换关系:

式 (2.3-28) 表示,周期性功率信号的互功率谱 C12 是其互相关函数 R12(τ) 的傅里叶级数的系数。若用傅里叶变换表示,式 (2.3-28) 可以改写为