信息学奥赛一本通 1552：【例 1】点的距离

【题目链接】

ybt 1552：【例 1】点的距离

【题目考点】

1. 最近公共祖先（LCA）：倍增求LCA

知识点讲解见：洛谷 P3379 【模板】最近公共祖先（LCA）

【解题思路】

首先用邻接表保存输入的无权图。
使用倍增求LCA的解题方法：设dep数组，$de{p}_u$表示顶点u的深度。设fa数组，$f{a}_{i,j}$表示从结点i开始向上走$2^j$步可以到达的结点。
而后对该图做深度优先遍历，可以预处理求出dep数组和fa数组，同时也将该图变为了有根树。
该图是无权图，可以认为每条边长度为1。
无权有根树上，根结点到一个结点的路径长度为该结点的深度（根结点深度为0）。
树上任意两结点之间存在唯一的路径。记结点x到结点y的路径长度为$Dis(x,y)$。
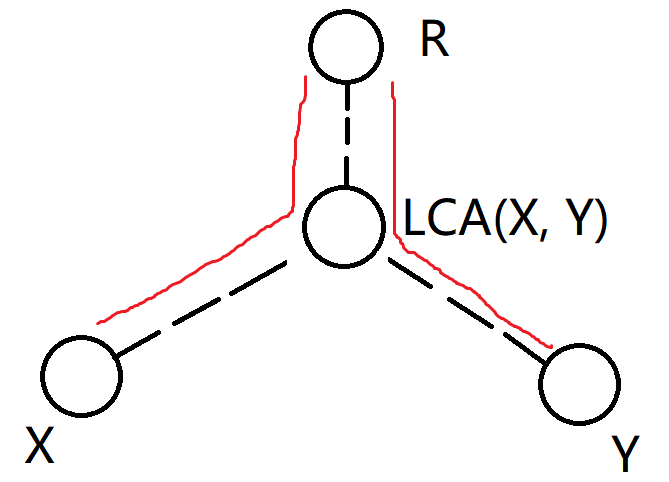
结点x到结点y的路径必然经过二者的最近公共祖先LCA(x, y)。
已知根结点r到x的路径长度为dep[x]，根结点r到y的路径长度为dep[y]。
根结点r到x的路径可以分为r到LCA(x,y)的路径，以及LCA(x, y)到x的路径。
根结点r到y的路径可以分为r到LCA(x,y)的路径，以及LCA(x, y)到y的路径。
二者相加后，总长度包括x到LCA(x, y)的路径长度，LCA(x, y)到y的路径长度，以及两倍的r到LCA(x, y)的路径长度。即x到y的路径长度加上两倍的LCA(x, y)的深度。
因此$de{p}_x+de{p}_y=Dis(x,y)+2de{p}_{LCA(x,y)}$
所以$Dis(x,y)=de{p}_x+de{p}_y-2de{p}_{LCA(x,y)}$

使用倍增求LCA算法，每次查询$Dis(x,y)$的时间复杂度为$O(\log n)$

【题解代码】

• 解法1：倍增求LCA

#include<bits/stdc++.h>
using namespace std;
#define N 100005
#define LN 25
vector<int> edge[N];
int n, lg[N], dep[N], fa[N][LN];//f[i][j]：顶点i向上走2^j到达的顶点 
void initLg()
{for(int i = 2; i <= n; ++i)lg[i] = lg[i/2]+1;
}
void dfs(int u)
{for(int v : edge[u]) if(v != fa[u][0])//v不是u的父亲 {fa[v][0] = u;dep[v] = dep[u]+1;for(int j = 1; 1<<j <= dep[v]; ++j)fa[v][j] = fa[fa[v][j-1]][j-1];dfs(v);}
}
int lca(int u, int v)
{if(dep[u] < dep[v])swap(u, v);while(dep[u] > dep[v])u = fa[u][lg[dep[u]-dep[v]]];if(u == v)//如果v本身为LCA(u, v)，那么当二者深度相同时，二者相同 return u;for(int k = lg[dep[u]]; k >= 0; --k)if(fa[u][k] != fa[v][k])u = fa[u][k], v = fa[v][k];return fa[u][0];
}
int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int q, x, y;cin >> n;for(int i = 1; i < n; ++i){cin >> x >> y;edge[x].push_back(y);edge[y].push_back(x);}initLg();dfs(1);cin >> q;while(q--){cin >> x >> y;cout << dep[x]+dep[y]-2*dep[lca(x, y)] << '\n';}return 0;
}