当前位置： 首页 > news >正文

估计随机行走的覆盖面积

news 2025/9/17 8:42:54

某次随机行走得到20个点，并把这20个点画到平面上

1

15

14

2

18

12

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

3

17

12

16

16

4

17

13

15

15

5

13

13

14

1

14

6

10

13

13

6

5

4

13

7

10

13

12

3

2

12

8

8

10

11

11

9

7

10

10

9

8

10

10

7

9

9

10

9

11

7

8

8

11

12

8

12

10

8

7

14

7

13

10

8

6

6

14

8

7

5

5

15

7

8

4

16

4

16

6

4

3

18

3

17

6

2

2

17

2

18

9

3

1

1

19

11

0

0

19

0

20

11

0

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

上下左右4点分别是1，19，16，2

这4个点围成的图形的面积为68，作为这次随机行走的面积。

 

设随机行走的移动步长r=2，a是一个[0,1),的随机数，移动的角度是360a，移动1，2，5，10万步得到面积为

2

360a

步数

总面积

平均

10000

7155.2

0.7155

20000

14111

0.7055

50000

34811

0.6962

100000

70904

0.709

由数据有理由猜测面积和步数之间的比值是一个常数

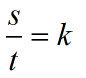
因为x和y的变化量为

x-x0=(int)(r*Math.cos(Math.PI*360*a/180) ) ;

y-y0=(int)(r*Math.sin(Math.PI*360*a/180) ) ;

java的（int）是向下取整

d

(int)d

-1.9

-1

-1.2

-1

-0.9

0

-0.2

0

0.2

0

0.9

0

1.2

1

1.9

1

因此x和y的变化量只有8种可能

sin

cos

30

-1

-1

210-240

60

-1

0

240-300

30

-1

1

300-330

60

0

-1

150-210

60

0

1

0--30

330-360

60

1

0

60-120

30

1

1

30-60

30

1

-1

120-150

由此得到单次移动的平均距离为

角度

sin

cos

距离

角度/360

占比

30

-1

-1

1.414

0.083333

0.1178

30

1

-1

1.414

0.083333

0.1178

30

1

1

1.414

0.083333

0.1178

30

-1

1

1.414

0.083333

0.1178

60

1

0

1

0.166667

0.1667

60

-1

0

1

0.166667

0.1667

60

0

-1

1

0.166667

0.1667

60

0

1

1

0.166667

0.1667

和

1.138

设单次移动形成一个锐角三角形，则360度随机取值平均值就是45度。以1.138为腰的等腰直角三角形的面积是1.138*1.138/2=0.6475，这个值是测量值的91.6%。

现在让单次移动的步长r=3，得到的数据为

3

360a

步数

总面积

平均

10000

24936

2.4936

20000

50521

2.526

50000

129536

2.5907

100000

254922

2.5492

首先统计角度占比

角度

sin

cos

6

-2

-2

222-228

11

-2

-1

229-240

59

-2

0

241-300

10

-2

1

301-311

6

-2

2

312-318

10

-1

-2

211-221

11

-1

2

319-330

59

0

-2

151-210

58

0

2

0-30

331-359

11

1

-2

139-150

10

1

2

31-41

6

2

-2

132-138

10

2

-1

121-131

59

2

0

61-120

11

2

1

49-60

6

2

2

42-48

精确到2位小数，计算单次移动的平均距离

角度

sin

cos

距离

角度/360

占比

6.37

-2

-2

2.828

0.017694

0.05

6.37

-2

2

2.828

0.017694

0.05

6.37

2

-2

2.828

0.017694

0.05

6.37

2

2

2.828

0.017694

0.05

11.8

-2

-1

2.236

0.032778

0.0733

11.8

-2

1

2.236

0.032778

0.0733

11.8

-1

-2

2.236

0.032778

0.0733

11.8

-1

2

2.236

0.032778

0.0733

11.8

1

-2

2.236

0.032778

0.0733

11.8

1

2

2.236

0.032778

0.0733

11.8

2

-1

2.236

0.032778

0.0733

11.8

2

1

2.236

0.032778

0.0733

60

-2

0

2

0.166667

0.3333

60

0

-2

2

0.166667

0.3333

60

0

2

2

0.166667

0.3333

60

2

0

2

0.166667

0.3333

和

2.12

等腰直角三角形的面积为2.12*2.12/2=2.24，这个值是实测值的88%。

步长r

2

3

平均距离

1.138

2.12

显然步长r越大，单次移动的距离越接近r。

让r=2，3，4，5，…，50得到数据

r

2

3

4

5

6

7

8

9

10

20

30

50

面积

0.7066

2.5399

5.4335

9.4481

14.76

20.65

27.914

36.027

46.044

196.68

456.9

1272.2

r*r/2

2

4.5

8

12.5

18

24.5

32

40.5

50

200

450

1250

比值

0.3533

0.5644

0.6792

0.7559

0.82

0.8428

0.8723

0.8896

0.9209

0.9834

1.0153

1.0178

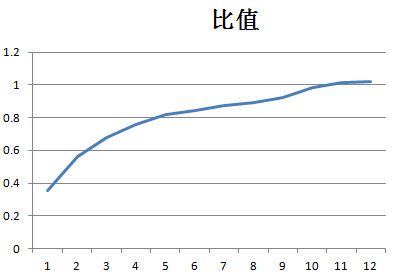
随着r变大，r*r/2得到的面积与测量得到的平均面积越接近。

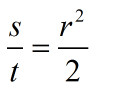
因此有理由猜测，当r足够大时，面积与步数的比就是步长平方的一半。

http://www.lryc.cn/news/570723.html

相关文章：

  • 基于NEON指令的图像旋转加速【armv7】
  • 基于ssm的学生作业管理系统
  • C#-从入门到精通-第12章 Windows应用程序高级控件
  • 如何使用deepseek编写测试计划
  • 科学计数法保留有效数字_分析化学中有效数字及其运算规则
  • C++题解(36) 2025年顺德区中小学生程序设计展示活动（初中组C++）换位（二）
  • 如何在ubuntu上安装flash_player
  • 本地安装discuz x2.5(论坛站)程序
  • BackTrack5(BT5)各版本下载
  • cd linux 镜像,解开 CDLinux 的iso映像文件
  • 战争
  • C语言空指针异常在Java中的解决方案
  • 各大搜索引擎网站提交入口
  • csdn博客登录不上-why?
  • mysql bulk update_Django bulk_create()、update()与数据库事务的效率对比分析
  • 超标量处理器设计9-执行
  • emule最新服务器地址,emule 国内服务器（最新emule服务器）
  • 关于2000W数据
  • 文件或目录损坏且无法读取怎么修复
  • Struts2中Action通配符的配置
  • [转]Linux下安装搜狗拼音输入法
  • 汇川SV660F伺服驱动器通过EtherCAT主站转Profinet网关接入到profinet系统
  • Qwen2.5-VL 是什么？
  • AI+预测3D新模型百十个定位预测+胆码预测+去和尾2025年6月15日第109弹
  • Linux下的优秀开源软件
  • css属性：图片使用filter属性使得position: fixed失效的情况
  • 如何使用github并且参与别人的开源项目
  • 用 Redis 都能实现哪些功能？这2万字+20张图给分析全了
  • WiFi基本知识
  • Nginx工作原理和优化总结。