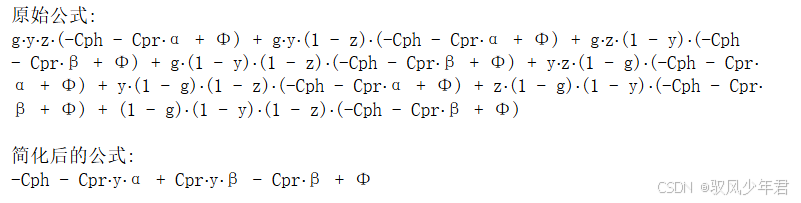【演化博弈】期望收益函数公式、复制动态方程——化简功能技巧
期望化简
在演化博弈论的研究中,期望收益函数和复制动态方程是核心工具。化简这些公式的功能技巧具有以下几个重要作用:
-
提高公式的可读性和理解度
复杂的数学表达式可能让人感到困惑。通过化简,公式变得更加简单和易读,使研究者能够更快地理解期望收益和策略动态的基本概念。这对于教学和研究都至关重要。 -
降低计算复杂度
在进行数值模拟或符号计算时,简化的表达式通常能显著减少计算量。这使得在处理复杂模型时,能够更高效地进行计算,减少计算资源的消耗。 -
揭示潜在的关系和模式
化简过程中,可能会发现原本复杂表达式中的重要关系和模式。这些新发现能够提供深入的见解,帮助研究者理解不同策略之间的相互作用。 -
便于推导和证明
在理论推导和证明过程中,化简公式可以使逻辑关系更加清晰,减少冗余步骤。这有助于提高论证的严谨性和说服力。
总结
化简【演化博弈】中期望收益函数公式和复制动态方程的功能技巧,不仅提高了公式的可读性和计算效率,还揭示了潜在关系,便于理论推导和实际应用。通过这些化简手段,研究者能够更深入地理解演化博弈的动态过程,从而在理论和实践中取得更好的成果。
用sympy中的simplify就可以实现这个函数化简
import sympy as sp# 定义变量
y, z, g, Φ, Cph, Cpr, α, β = sp.symbols('y z g Φ Cph Cpr α β')# 定义公式
Ux = (y*z*g*(Φ - Cph - α*Cpr) +y*z*(1 - g)*(Φ - Cph - α*Cpr) +y*(1 - z)*g*(Φ - Cph - α*Cpr) +y*(1 - z)*(1 - g)*(Φ - Cph - α*Cpr) +(1 - y)*z*g*(Φ - Cph - β*Cpr) +(1 - y)*z*(1 - g)*(Φ - Cph - β*Cpr) +(1 - y)*(1 - z)*g*(Φ - Cph - β*Cpr) +(1 - y)*(1 - z)*(1 - g)*(Φ - Cph - β*Cpr))# 简化公式
simplified_Ux = sp.simplify(Ux)# 输出结果
print("原始公式:")
sp.pprint(Ux)
print("\n简化后的公式:")
sp.pprint(simplified_Ux)