编译原理复习---正则表达式+有穷自动机
适用于电子科技大学编译原理期末考试复习。
1. 正则表达式
正则表达式(Regular Expression,简称regex或regexp)是一种用于描述、匹配和操作文本模式的强大工具。它由一系列字符和特殊符号组成,这些字符和符号定义了一种搜索模式,可以用来检查一个字符串是否包含某个子串、将匹配的子串进行替换或者从字符串中提取符合条件的子串等。
总结来说,正则表达式就是通过特定字符与文法符号的组合来描述一种语言的方式。
正则语言 == 上下文无关文法 == 正则表达式,三者之间可以相互转换
编译原理这门课中,正则表达式所使用的符号与标准的定义好像不太相同,我只能凭借做题的经验列举出大致的用法:
:表示集合{
,
,...,
}中的任意一个字符。
每一个单元(正则表达式中的一个字符或用括号包围起来的一组符号)后可加上" * "(克林闭包)、" + "(正闭包)。
" . "表示字母表中的任意字符。
例如:
2. 有穷自动机
有穷自动机(Finite Automaton, FA),也称为有限状态机,是一种计算模型,用于描述和识别特定类型的语言。它由以下几个基本组成部分构成:
状态集合(Q):有限个状态的集合。
字母表(Σ):有限个输入符号的集合。
转移函数(δ):定义了从一个状态和一个输入符号到另一个状态的映射,即 δ: Q × Σ → Q。
初始状态(q0):自动机开始处理输入前所在的状态,q0 ∈ Q。
接受状态集(F):状态集合的一个子集,表示当自动机停止时可以处于的状态,这些状态表明输入字符串被接受,F ⊆ Q。
通常,我们使用状态转换图来表示有穷自动机:

有穷自动机可以分为确定型有穷自动机(Deterministic Finite Automaton, DFA)和非确定型有穷自动机(Nondeterministic Finite Automaton, NFA)。
DFA的每一步操作都是确定的,即对于一个状态和一个输入符号,有唯一确定的下一个状态。

而NFA在某些状态下,对于一个输入符号可能有多个可能的下一个状态。
相对于DFA,NFA更加直观,但是对于计算机来说,DFA才方便其使用。
我们要将正则表达式转换为DFA并不好转换,可以先将其转换为更加直观的NFA,然后再将NFA转换为DFA。
3. 正则表达式转换为NFA
3.1 单个符号的NFA

3.2 (a|b)的NFA,并联
 3.3 ab的NFA,串联
3.3 ab的NFA,串联

3.4 a*的NFA
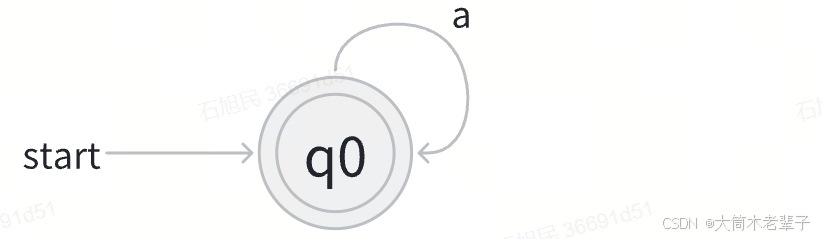
通过以上四种方式,我们可以逐步将一个正则表达式转换为NFA。
4. NFA转化为DFA
初始状态在遇到某个输入符号时能进入的所有状态的集合定义为一个新的状态,在DFA的状态图中,初始状态指向该新状态。
对每个输入符号都进行检查,定义出一系列新的状态。
对于每个新状态,将其当作初始状态并重复上面两步,直到不再有新状态产生。
注意,当通过某个输入符号到达某一状态时,新到达的状态如果可以通过空边到达其他状态,那么也视为在遇到该输入符号时能到达这些状态。
如果初始状态可以通过空边到达其他状态,那么应该把这几个状态连同初始状态当作DFA中的初始状态。
举例子太费劲了,就不举了。
