机器学习3_支持向量机_线性不可分——MOOC
线性不可分的情况
如果训练样本是线性不可分的，那么上一节问题的是无解的，即不存在 和
满足上面所有N个限制条件。
对于线性不可分的情况，需要适当放松限制条件，使得问题有解。
放松限制条件的基本思路：
对每个训练样本及标签
设置松弛变量（slack variable）
对于线性不可分情况，需适当放松限制条件
限制条件改写：
改造后的支持向量机优化版本
最小化： 或
限制条件：
（1）
（2）
- 以前的目标函数只需要最小化
，现在的目标函数增加了一项 所有
的和。
- 比例因子
平衡两项
比例因子 是人为设定的。
人为事先设定的参数叫做算法的超参数（Hyper Parameter）
实际中：不断变化 的值
同时测试算法的识别率
选取超参数
一个算法中，选取的超参数 越多，意味着算法需要手动调整优化的地方也就越多，这样算法的自动性也会降低。
支持向量机是超参数很少的算法模型。
超参数很多的算法模型，如人工神经网络、卷积神经网络等。
在线性不可分情况下应用支持向量机
取目标函数：
是为了超平面和线性可分情况保持基本一致
以下是训练数据以及解出的分类面的展示
可以看到这个分类面分开大多数的圆圈和叉，只在一个训练样本上存在分类的错误。
有了线性不可分情况下的支持向量机算法
如图，这个解分错了将近一半的样本，这个解远远不能让人满意。
问题在于我们的算法模型是线性的。也就是，我们假设分开两类的函数是直线或者超平面，我们是在一组直线和超平面中选择最合适分开这两类数据的直线或者超平面。但线性模型的表现力是不够的。
在下图这个例子中，可以看到能够分开这两类的是某种曲面，例如这个椭圆，而不是直线。
因此，我们只有想办法扩大可选函数的范围，使它超越线性，才有可能应对各种复杂的线性不可分的情况。
低维到高维的映射
支持向量机在扩大可选函数范围方面独树一帜。
其他算法，如人工神经网络、决策树等，采用的是直接产生更多可选函数的方式。
例如上图，在人工网络中，通过多层非线性函数的组合能够产生类似于椭圆这样的曲线，从而分开这幅图中的圆圈和叉。
而支持向量机却不是直接产生这样的函数，而是通过将特征空间由低维映射到高维，然后在高维的特征空间当中用线性超平面对数据进行分类。
、
是图中的❌，
、
是图中的⭕️
这个例子是线性不可分的
如果我们构造一个二维到五维到映射
按照这个映射，可以解出、
、
、
当映射变成五维时，、
、
、
线性可分
设：
可以算出
由于、
是同一类，
、
是同一类
人为二维到五维到映射 ，线性不可分的数据集
线性可分的数据集
假设：
在一个M维空间上随机取N个训练样本，随机的对每个训练样本赋予标签
或
假设：
这些训练样本线性可分的概率为
则
当
趋于无穷大时，
即，当我们增加特征空间的维度 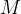的时候，超平面待估计的参数 
的维度也会增加。也就是整个算法模型的自由度会增加。
这个定理告诉我们，将训练样本由低维映射到高维 增大线性可分的概率。