深度学习:简单计算图的反向传播传递导数计算
问题:
太郎在超市买了2个100日元一个的苹果,消费税是10%,请计算支付金额。
 反向传播使用与正方向相反的箭头(粗线)表示。反向传播传递“局部导数”,将导数的值写在箭头的下方。在这个例子中,反向传播从右向左传递导数的值(1 → 1.1 → 2.2)。从这个结果中可知,“支付金额关于苹果的价格的导数”的值是2.2。这意味着,如果苹果的价格上涨1日元,最终的支付金额会增加2.2日元。
反向传播使用与正方向相反的箭头(粗线)表示。反向传播传递“局部导数”,将导数的值写在箭头的下方。在这个例子中,反向传播从右向左传递导数的值(1 → 1.1 → 2.2)。从这个结果中可知,“支付金额关于苹果的价格的导数”的值是2.2。这意味着,如果苹果的价格上涨1日元,最终的支付金额会增加2.2日元。
讲解:
反向传播的目的是计算支付金额关于苹果价格的导数。我们从右向左传递导数的值。
步骤1:支付金额关于消费税的导数
支付金额是苹果总价加上消费税,所以支付金额关于消费税的导数是1。
∂支付金额/∂消费税=1
∂支付金额/∂苹果总价=1
步骤2:消费税关于苹果总价的导数
消费税是苹果总价的10%,所以消费税关于苹果总价的导数是0.1。
∂消费税/∂苹果总价=0.1
步骤3:苹果总价关于苹果单价的导数
苹果总价是2个苹果的价格之和,所以苹果总价关于苹果价格的导数是2。
∂苹果总价/∂苹果单价=2
-
反向传播传递导数的值
支付金额 = 苹果总价 + 消费税
消费税 = 苹果总价*0.1
我们从右向左传递导数的值:支付金额关于 支付金额的导数是1
支付金额关于苹果总价的导数是
∂支付金额/∂苹果总价 + ∂支付金额/∂消费税 * ∂消费税/∂苹果总价 = 1 + 0.1 = 1.1支付金额关于苹果单价的导数是
∂支付金额/∂苹果总价 * ∂苹果总价/∂苹果单价+ ∂支付金额/∂消费税 * ∂消费税/∂苹果总价 * ∂苹果总价/∂苹果单价 = 1 * 2 + 1 * 0.1 * 2 = 2.2 这是正常算法
向前传递的话会更简便
可以直接用 支付金额关于苹果总价的导数 * ∂苹果总价/∂苹果单价 ,这样会使计算导数更为高效 即1.1*2 = 2.2
从这个结果中可知,“支付金额关于苹果的价格的导数”的值是2.2。这意味着,如果苹果的价格上涨1日元,最终的支付金额会增加2.2日元。
补两个知识点:
1、乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游,
如下图所示:
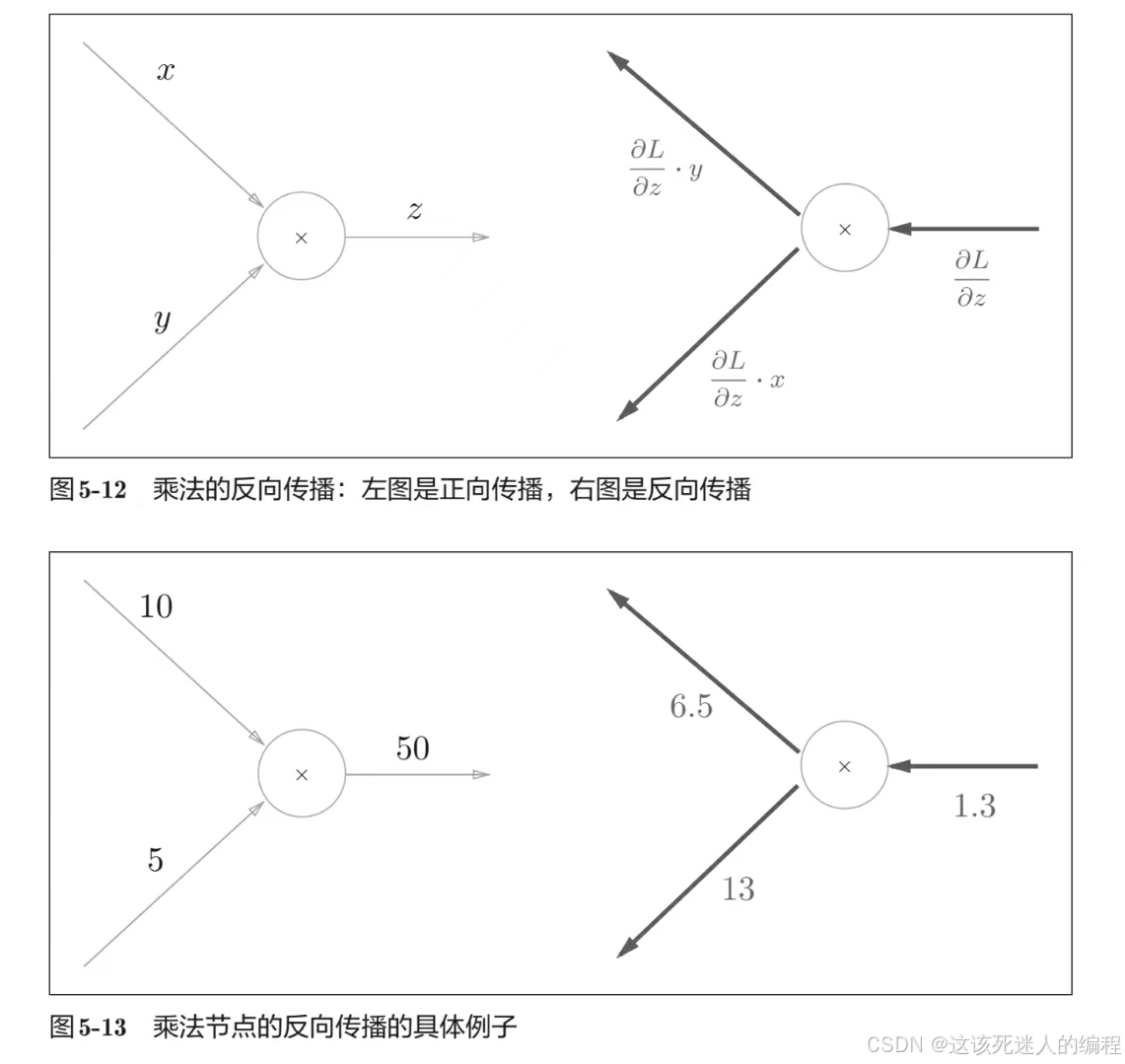 因此,实现乘法节点的反向传播时,要保存正向传播的输入信号。
因此,实现乘法节点的反向传播时,要保存正向传播的输入信号。
而一开始的问题中求“支付金额关于苹果的价格的导数”“支付金额关于苹果的个数的导数”“支付金额关于消费税的导数”。用计算图的反向传播来解的话,求解过程如下图:
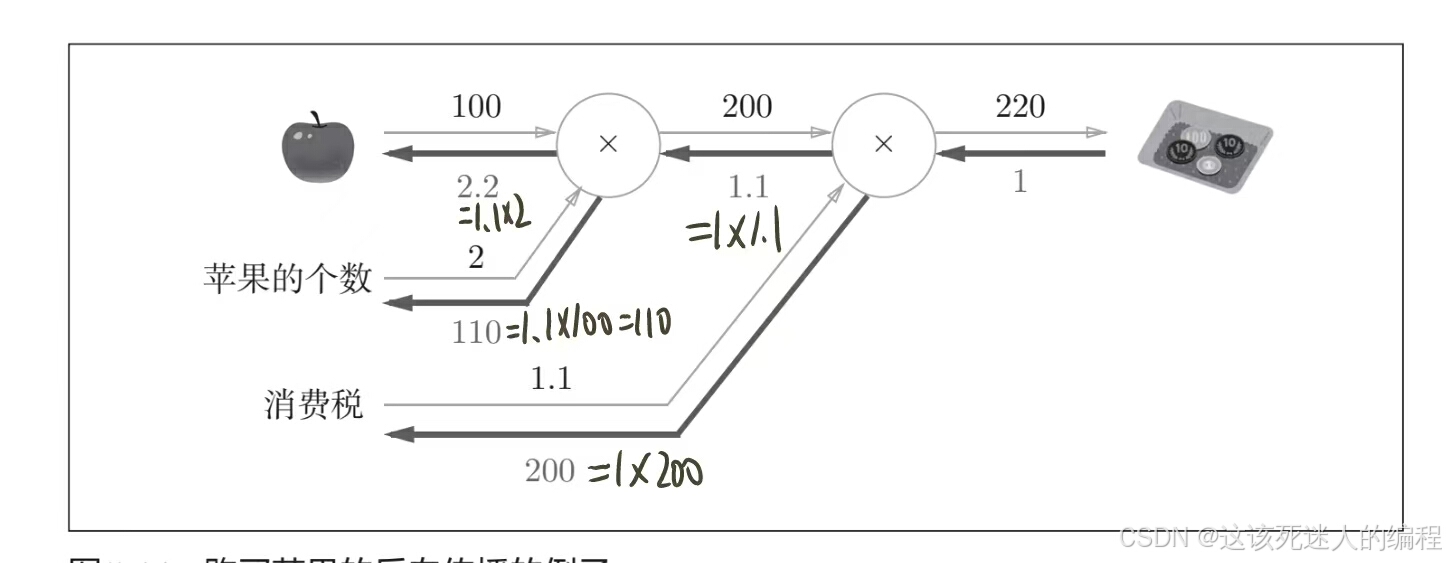 可以很快求解。
可以很快求解。
2、加法节点的反向传播只乘以1,所以输入的值会原封不动地流向下一个节点,
如下图所示:
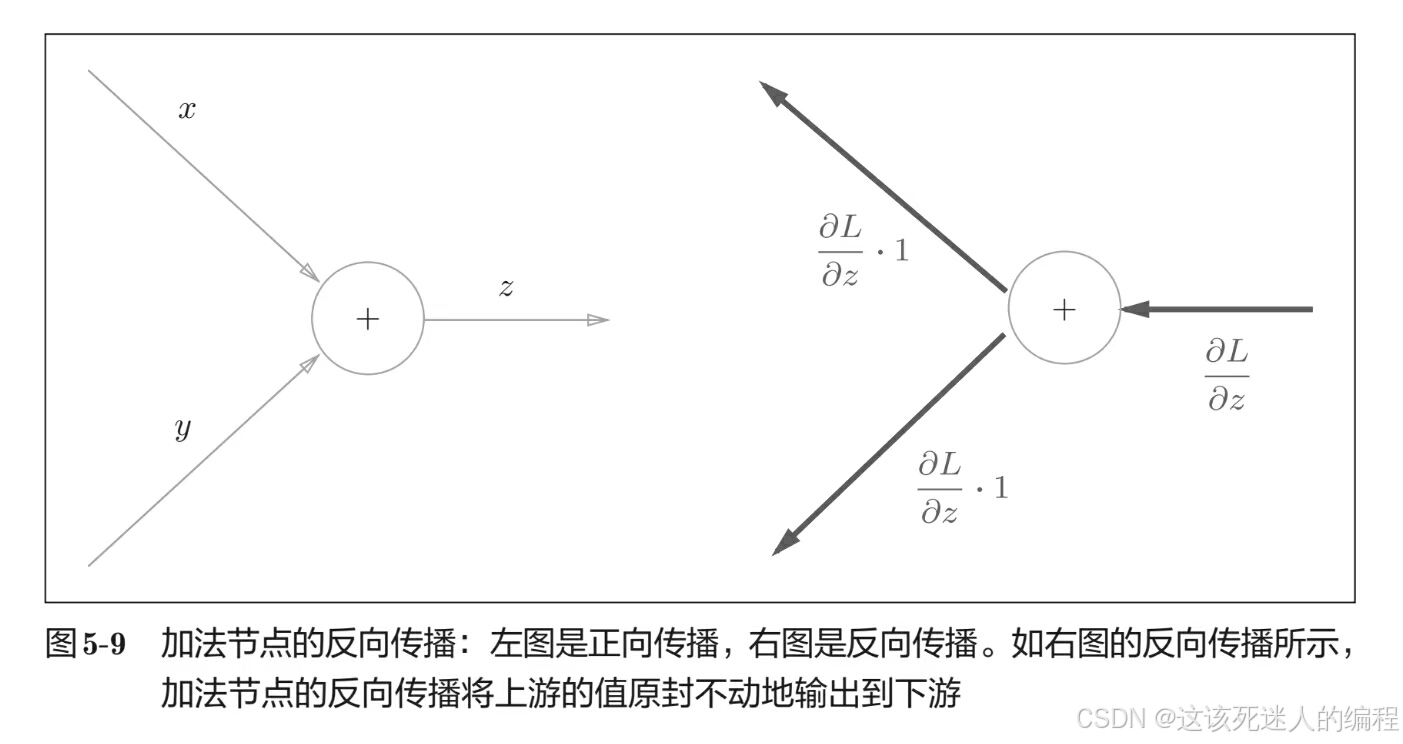
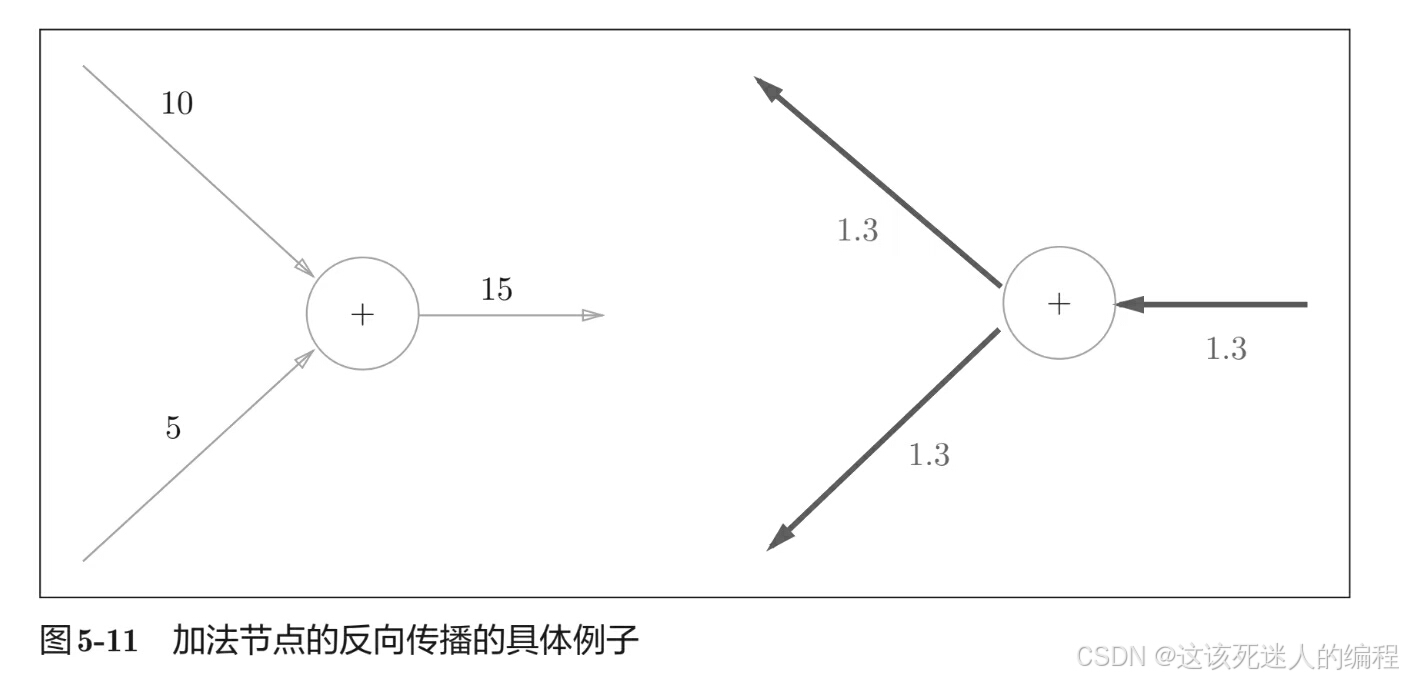
 文章开头的问题代码实现:
文章开头的问题代码实现:
定义乘法层:
class MulLayer:def __init__(self):self.x = Noneself.y = Nonedef forward(self, x, y):self.x = xself.y = yout = x * yreturn outdef backward(self, dout):dx = dout * self.ydy = dout * self.xreturn dx, dy
apple = 100
apple_num = 2
tax = 1.1mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax)
print(price)
运行结果:220.00000000000003
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)
print(dapple, dapple_num, dtax)
运行结果:2.2 110.00000000000001 200
