1282:最大子矩阵
题目:
已知矩阵的大小定义为矩阵中所有元素的和。给定一个矩阵,你的任务是找到最大的非空(大小至少是1 × 1)子矩阵。
比如,如下4 × 4的矩阵
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
的最大子矩阵是
9 2
-4 1
-1 8
这个子矩阵的大小是15。
【输入】
输入是一个N×N的矩阵。输入的第一行给出N(0<N≤100)。再后面的若干行中,依次(首先从左到右给出第一行的N个整数,再从左到右给出第二行的N个整数……)给出矩阵中的N2个整数,整数之间由空白字符分隔(空格或者空行)。已知矩阵中整数的范围都在[−127,127]。
【输出】
输出最大子矩阵的大小。
【输入样例】
4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
【输出样例】
15
题意:
找出梓矩阵最大和
思路:
-
暴力模拟就是就是遍历求x1-x2行最值,再遍历y1-y2列的最值, 四层循环容易超时
-
-只看一行求最值就是最大连续子序列,但是有很多行,现在求未知连续的k行的矩阵,所以就需要遍历1-2,1-3,1-4,2-3,2-4行,,,,
-
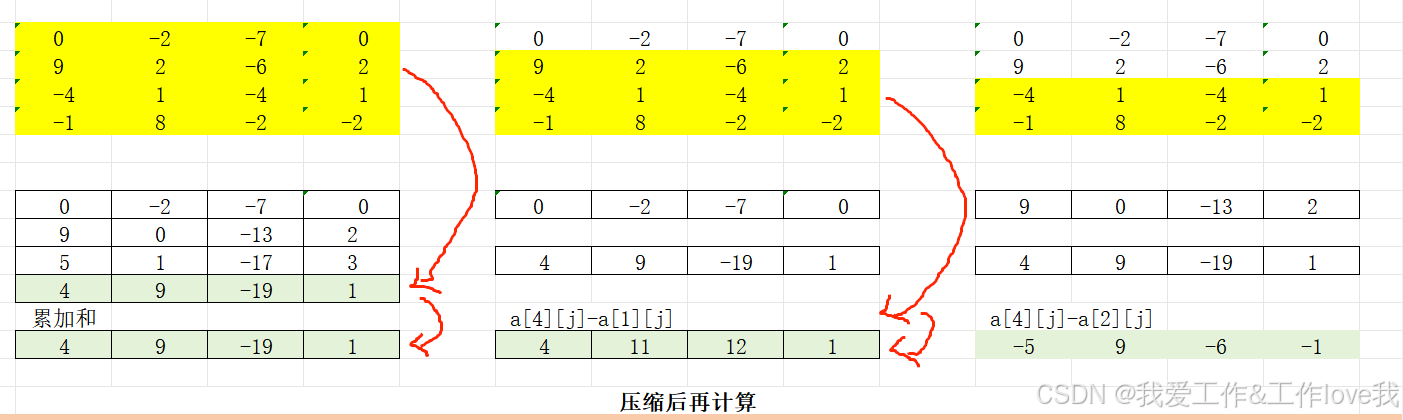
求矩阵和,所以利用前缀和的知识,可以累加前一行的数据直到最后一行,要求区间K行的子矩阵遍历即可-即要求k行直接压缩成一维数组,变成了一个一维数组的最长子序列问题
-
确定状态/选择:累加行/列以后直接利用最大字段和的做法 dp[i] = max(dp[i-1]+k,dp[i])
-
确定状态转移方程
-
边界条件:
-①dp都初始化为0,每次遍历完两行,求出矩阵和,计算了dp数组后求出当前的最值,dp初始化一下。
②存储最值的变量应该初始化:<-128 因为数据范围在【-127,127】。
③遍历时,后一行减去前一行,所以i 为【1,n】,j为【1,n】,j不能是【i+1,n】,因为有可能矩阵第一行就是有最值!
数据约束:
无
注意:
①:数组边界/遍历范围要注意!!
②:数据初始化要注意数据边界
参考代码一
#include<bits/stdc++.h>
#define N 105
using namespace std;
int a[N][N],dp[N],ans=-128; //初始化#。。。。。。。。。。! int main(){int n;cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];a[i][j] += a[i-1][j];//各行的值累加 }} for(int i=1;i<=n;i++){ //开始行 for(int j=i;j<=n;j++){ //结束行 for(int k=1;k<=n;k++){ //处理两行之前列的数据-做最大连续子序列 dp[k] = a[j][k]-a[i-1][k];dp[k] = max(dp[k],dp[k-1]+a[j][k]-a[i-1][k]); //选择两行 并处理dp数组ans = max(ans,dp[k]); }memset(dp,0,sizeof(dp));}} cout<<ans;return 0;}
参考代码二
#include<bits/stdc++.h>
#define N 105
using namespace std;
N],dp[N],ans=-128; //初始化#。。。。。。。。。。! int main(){int n;cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];a[i][j] += a[i][j-1];//各列的值累加}} for(int i=1;i<=n;i++){ //开始列 for(int j=i;j<=n;j++){ //结束列 不能从第二行开始,不然第一行怎么办!! memset(dp,0,sizeof(dp));for(int k=1;k<=n;k++){ //处理两列之前列的数据-做最大连续子序列 dp[k] = a[k][j]-a[k][i-1];dp[k] = max(dp[k],dp[k-1]+a[k][j]-a[k][i-1]); //选择两行 并处理dp数组ans = max(ans,dp[k]); }}} cout<<ans;return 0;}
