当前位置：首页 > news >正文

【算法题】62. 不同路径(LeetCode)

news 2025/8/19 7:33:27

【算法题】62. 不同路径(LeetCode)

1.题目

下方是力扣官方题目的地址

62. 不同路径

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：
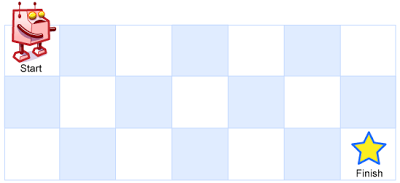
```
输入：m = 3, n = 7
输出：28
```
示例 2：
```
输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
```
示例 3：
```
输入：m = 7, n = 3
输出：28
```
示例 4：
```
输入：m = 3, n = 3
输出：6
```
提示：
- 1 <= m, n <= 100
- 题目数据保证答案小于等于 2 * 109

2.题解

思路一(公式)

机器人无论怎么走到终点，向下向右的步数是固定的，都是向右n-1格，向下m-1格。

所以我们可以使用组合数，一共走m+n-2次，再其中选出m-1次向下走，其余的自然就是向右走了，所以有：

所以有
$C (m + n - 2, m - 1)$
如何计算它呢？

$\frac{n!}{k!(n-k)!}$

所以有：

Python代码

class Solution(object):def uniquePaths(self, m, n):""":type m: int:type n: int:rtype: int"""from math import factorialreturn factorial(m+n-2)//(factorial(m-1)*factorial(n-1))

思路二(深度优先)

我们有深度优先搜索模拟所有情况，然后来个计数器计数

Python代码

class Solution(object):def uniquePaths(self, m, n):""":type m: int:type n: int:rtype: int"""global ansans=0def dfs(d,x,y):             # d 为深度global ansif d==(m+n-2):ans+=1returndirec=[[1,0],[0,1]]     # 向下或者向右for dx,dy in direc:if 0<=x+dx<m and 0<=y+dy<n:dfs(d+1,x+dx,y+dy)dfs(0,0,0)return ans

这种思路好想到，不过显然超时了

在这里插入图片描述

思路三(动态规划)

我们用dp[i][j]表示到达位置(i,j)时的总路径数。

很显然，当i=0或者j=0时，总路径数都是1

先把这些情况预处理了

其他情况遵循状态转移方程：

dp[i][j]=dp[i-1][j]+dp[i][j-1]

即当前位置的总数是它上方和左方总数之和

Python代码

class Solution(object):def uniquePaths(self, m, n):""":type m: int:type n: int:rtype: int"""dp=[[0]*n for _ in range(m)]    # 初始化dp数组for i in range(n):dp[0][i]=1                  # 预处理for i in range(m):dp[i][0]=1for i in range(1,m):for j in range(1,n):dp[i][j]=dp[i-1][j]+dp[i][j-1]return dp[-1][-1]