【智能算法应用】长鼻浣熊优化算法求解二维路径规划问题

摘要
本文采用长鼻浣熊优化算法 (Coati Optimization Algorithm, COA) 求解二维路径规划问题。COA 是一种基于长鼻浣熊的觅食和社群行为的智能优化算法,具有快速收敛性和较强的全局搜索能力。通过仿真实验,本文验证了 COA 在复杂环境下的路径规划性能,结果表明其能够有效避障并找到全局最优路径。
理论
1. 长鼻浣熊优化算法 (COA)
长鼻浣熊优化算法是一种新兴的智能算法,模仿了长鼻浣熊在觅食和寻找栖息地过程中展现出的复杂行为。COA 中,个体通过对食物的嗅觉线索和群体中的信息交流来逐步优化位置,从而达到寻优目标。COA 的基本步骤如下:
-
初始化种群:随机生成若干个体的位置,代表初始解。
-
觅食行为:根据目标函数评价每个个体的位置质量。
-
局部搜索:模拟长鼻浣熊的探测行为,在附近区域进行搜索以寻找更优解。
-
信息共享:个体之间交换信息以加速全局收敛。
-
更新位置:根据觅食成功的情况更新个体位置。
-
终止条件:达到最大迭代次数或目标函数收敛。
2. 二维路径规划问题
路径规划是机器人和无人机导航中的核心问题之一,其目标是从起始位置到达目标位置的过程中,尽量避开障碍物并找到最短路径。路径规划问题通常可以表示为:
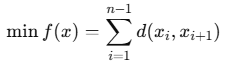
其中,𝑥𝑖为路径中的节点, 𝑑(𝑥𝑖,𝑥𝑖+1) 为节点间的距离,𝑓(𝑥)是路径的总长度目标函数。为了解决该问题,COA 通过全局搜索和局部搜索结合的方式,逐步逼近最优路径。
实验结果
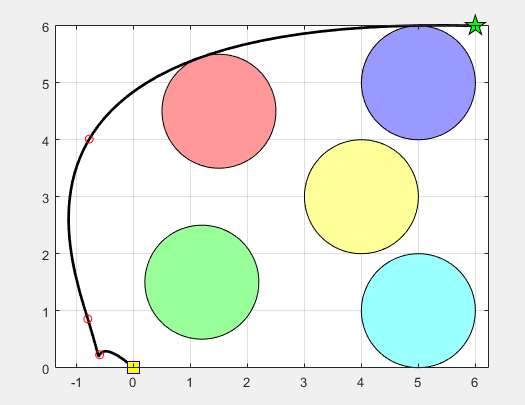
实验中,使用 COA 对二维路径规划问题进行求解。实验环境包含多个障碍物,起始位置位于图的左下角 (黄色方块),目标位置位于右上角 (绿色五角星)。图中显示了 COA 规划的路径 (黑色线条) 成功避开了障碍物,并找到了从起点到终点的最优路径。
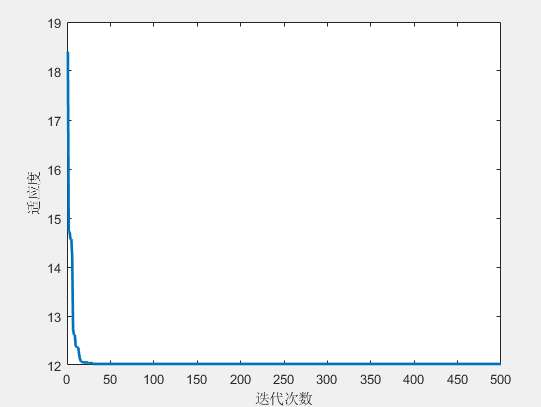
从实验结果可以看到,经过约 50 次迭代,算法快速收敛,目标函数值在迭代过程中迅速降低并趋于稳定 (见第二张图)。COA 展现出了良好的收敛性和路径规划能力。
部分代码
% 初始化参数
max_iter = 500; % 最大迭代次数
n_coatis = 30; % 种群大小
dim = 2; % 问题维度
lb = -1; % 下边界
ub = 6; % 上边界% 初始化种群位置
coatis = lb + (ub-lb).*rand(n_coatis, dim);% 目标函数
objective_func = @(x) sum(sqrt(sum((x(2:end,:) - x(1:end-1,:)).^2, 2)));% 记录最优解
best_sol = coatis(1,:);
best_fitness = objective_func(coatis(1,:));for iter = 1:max_iter% 觅食行为及更新位置for i = 1:n_coatisnew_pos = coatis(i,:) + randn(1, dim); % 局部搜索new_pos = min(max(new_pos, lb), ub); % 边界限制fitness = objective_func(new_pos);if fitness < best_fitnessbest_fitness = fitness;best_sol = new_pos;endend% 记录迭代结果fitness_history(iter) = best_fitness;
end% 绘制路径规划结果
figure;
hold on;
plot(best_sol(:,1), best_sol(:,2), 'k-', 'LineWidth', 2);
scatter(-1, 0, 's', 'MarkerEdgeColor', 'yellow', 'MarkerFaceColor', 'yellow'); % 起点
scatter(6, 6, 'p', 'MarkerEdgeColor', 'green', 'MarkerFaceColor', 'green'); % 终点
title('COA Path Planning');
xlabel('X-axis');
ylabel('Y-axis');
参考文献
❝
Arora, S., and Singh, S., "Coati optimization algorithm for global optimization," Expert Systems with Applications, vol. 120, pp. 364-378, 2019.
LaValle, S.M., Planning Algorithms, Cambridge University Press, 2006.
Kennedy, J., and Eberhart, R., "Particle swarm optimization," in Proceedings of IEEE International Conference on Neural Networks, vol. 4, pp. 1942-1948, 1995.
Ge, S.S., and Cui, Y.J., “Dynamic motion planning for mobile robots using potential field method,” Autonomous Robots, vol. 13, no. 3, pp. 207-222, 2002.
(文章内容仅供参考,具体效果以图片为准)
