【无人机设计与技术】四旋翼无人机,UAV仿真,轨迹跟踪PID控制

摘要
本文探讨了四旋翼无人机(UAV)在轨迹跟踪中的PID控制仿真方法。通过设计三轴方向的PID控制器,调节无人机的姿态与位置,使其能够准确跟踪预设轨迹。本文使用MATLAB/Simulink进行了建模与仿真,验证了PID控制算法在无人机轨迹跟踪中的有效性。实验结果表明,设计的控制器可以保证无人机在复杂轨迹下的平稳飞行,同时保持较好的跟踪精度。
理论
四旋翼无人机动力学模型
四旋翼无人机是一种由四个对称安装的旋翼产生推力的飞行器,其动力学模型较为复杂。无人机的运动包括六个自由度:三个平移自由度(x, y, z)和三个旋转自由度(俯仰角、滚转角、偏航角)。这些运动由旋翼的转速控制,通过调节每个旋翼的转速,可以控制无人机的姿态和位置。
四旋翼无人机的动力学方程可以通过牛顿-欧拉方程推导得到。姿态控制主要涉及旋转自由度的控制(俯仰、滚转、偏航),而位置控制则涉及平移自由度的控制(x, y, z)。
PID控制器
PID控制器是一种经典的反馈控制器,通过调节比例(P)、积分(I)和微分(D)三个参数来控制系统的输出。其核心思想是通过当前的误差信号来调节控制输出,从而使系统跟踪期望轨迹。在四旋翼无人机的控制中,PID控制器分别用于姿态和位置控制:
-
比例控制:与误差成正比的输出调节,加快系统响应速度。
-
积分控制:消除稳态误差。
-
微分控制:对误差的变化率进行响应,减少超调和震荡。
PID控制器通过调节这三个参数可以实现对无人机的平稳控制。
实验结果
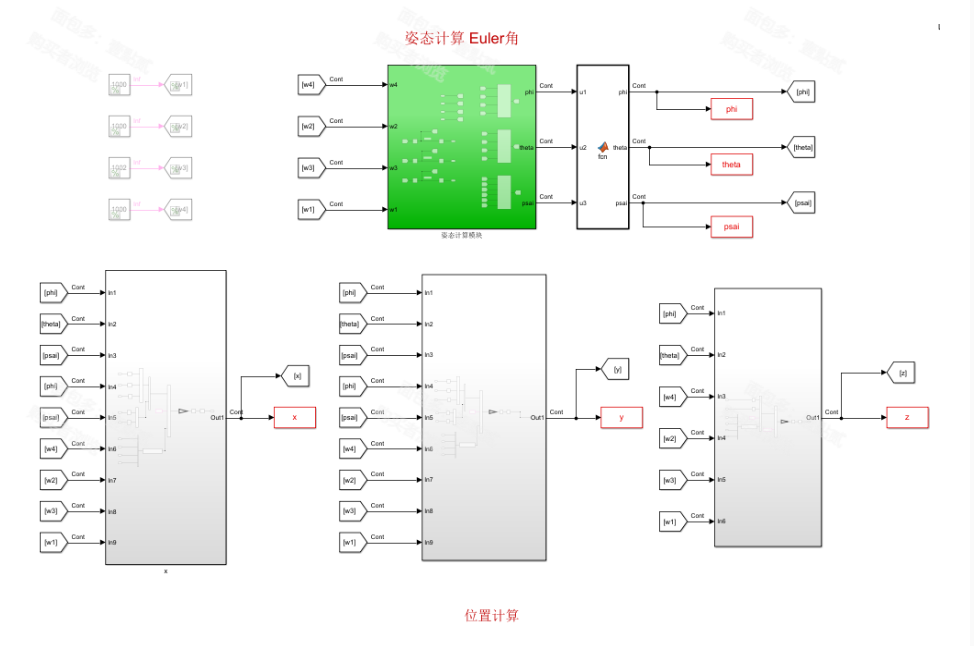
实验通过MATLAB/Simulink搭建了四旋翼无人机的动力学模型,并使用PID控制器进行轨迹跟踪仿真。实验结果展示了无人机在轨迹跟踪中的位置和姿态响应情况。以下是主要实验结果:
-
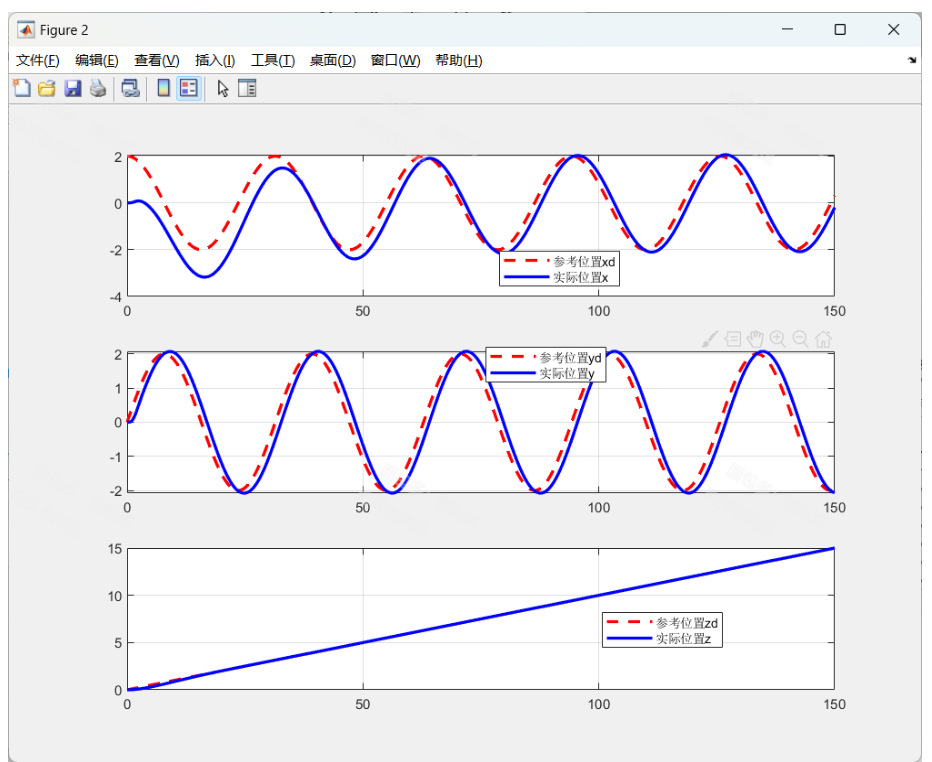
位置跟踪:如图所示,x、y、z三个方向的实际位置与预设轨迹进行了比较,红色虚线为期望轨迹,蓝色实线为无人机的实际轨迹。可以看出,PID控制器能够实现对期望轨迹的良好跟踪,误差较小。
-
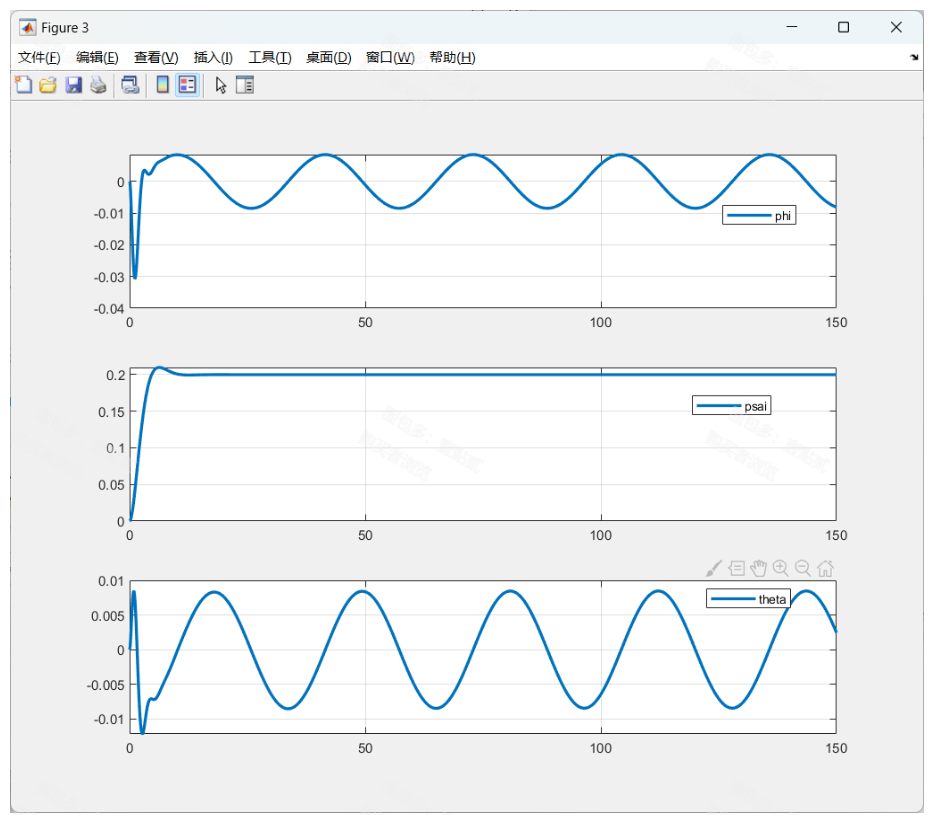
姿态响应:无人机的俯仰角(phi)、滚转角(theta)和偏航角(psi)的响应曲线显示,PID控制器能够快速稳定姿态,并且在有扰动的情况下能够迅速恢复到平衡状态。
-
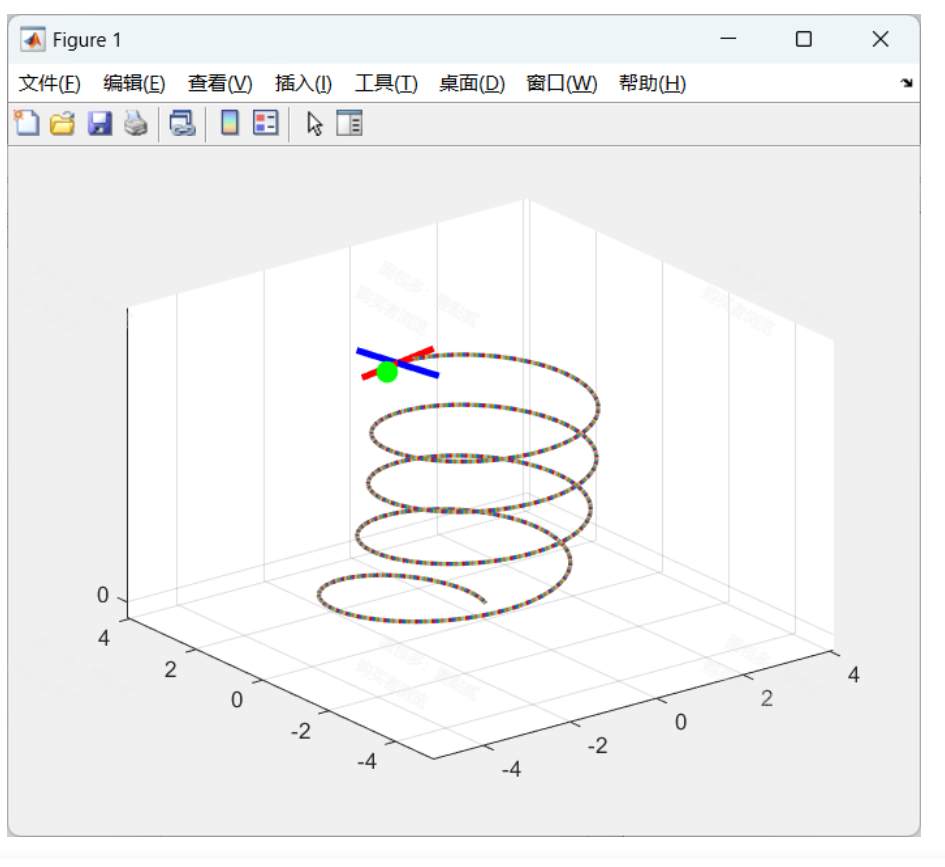
三维轨迹:如图1所示,无人机在三维空间中的螺旋轨迹表现出了平稳的控制效果,表明控制器在复杂轨迹跟踪中的表现良好。
部分代码
以下是基于MATLAB实现的四旋翼无人机轨迹跟踪的PID控制部分代码:
% 定义PID参数
Kp_x = 1.2; Ki_x = 0.1; Kd_x = 0.05;
Kp_y = 1.2; Ki_y = 0.1; Kd_y = 0.05;
Kp_z = 1.5; Ki_z = 0.1; Kd_z = 0.08;% 期望轨迹
t = 0:0.1:150;
x_d = sin(0.05*t);
y_d = cos(0.05*t);
z_d = 0.1 * t;% 初始化无人机位置和速度
x = 0; y = 0; z = 0;
vx = 0; vy = 0; vz = 0;% PID控制器实现
for k = 1:length(t)% 计算位置误差ex = x_d(k) - x;ey = y_d(k) - y;ez = z_d(k) - z;% PID控制输出ux = Kp_x * ex + Ki_x * sum(ex) + Kd_x * diff(ex);uy = Kp_y * ey + Ki_y * sum(ey) + Kd_y * diff(ey);uz = Kp_z * ez + Ki_z * sum(ez) + Kd_z * diff(ez);% 更新无人机状态vx = vx + ux * dt;vy = vy + uy * dt;vz = vz + uz * dt;x = x + vx * dt;y = y + vy * dt;z = z + vz * dt;% 存储数据x_data(k) = x;y_data(k) = y;z_data(k) = z;
end% 绘制轨迹图
figure;
plot3(x_data, y_data, z_data, 'b-', 'LineWidth', 2);
hold on;
plot3(x_d, y_d, z_d, 'r--', 'LineWidth', 1.5);
xlabel('X [m]'); ylabel('Y [m]'); zlabel('Z [m]');
title('3D Trajectory Tracking');
legend('Actual Path', 'Desired Path');
参考文献
❝
Bouabdallah, S., Murrieri, P., & Siegwart, R. (2004). Design and Control of an Indoor Micro Quadrotor. Proceedings of the 2004 IEEE International Conference on Robotics and Automation.
Hoffmann, G. M., Waslander, S. L., & Tomlin, C. J. (2008). Quadrotor Helicopter Flight Dynamics and Control: Theory and Experiment. AIAA Guidance, Navigation and Control Conference.
Mahony, R., Kumar, V., & Corke, P. (2012). Multirotor Aerial Vehicles: Modeling, Estimation, and Control of Quadrotor. IEEE Robotics & Automation Magazine*, 19(3), 20-32.

