【算法】反向传播算法
David Rumelhart 是人工智能领域的先驱之一,他与 James McClelland 等人在1986年通过其著作《Parallel Distributed Processing: Explorations in the Microstructure of Cognition》详细介绍了反向传播算法(Backpropagation),这一算法为多层神经网络的训练提供了有效的途径,是深度学习发展的重要里程碑之一。
反向传播算法的核心思想:
反向传播(Backpropagation)算法是基于梯度下降法的一种优化算法,用来训练多层感知器(MLP)等神经网络模型。它的主要思想是,通过逐层计算误差的梯度,并向网络的反方向传播这些误差,更新神经网络的权重,以最小化损失函数。
以下是反向传播算法的基本步骤及其对应的数学公式:
一、前向传播(Forward Propagation)
前向传播的目的是计算神经网络的输出。对于第 l 层的线性组合和激活值:
1. 线性组合:

这里,W(l) 是权重矩阵,a(l−1) 是第 l−1 层的激活值,b(l) 是偏置项。
2. 激活值:
然后通过激活函数 g,得到第 l 层的激活值:

二、 损失函数计算(Loss Function Calculation)
网络的输出和真实标签(目标值)之间的差异通过损失函数来度量。例如,对于回归问题常用均方误差(MSE),对于分类问题常用交叉熵损失(Cross Entropy)。假设损失函数为 L,我们的目标是最小化 L。
三、 反向传播(Backpropagation)
在反向传播阶段,我们通过链式法则计算损失函数对各层权重 W(l) 和偏置 b(l) 的梯度,即:

这些梯度表示每个权重和偏置对最终损失 L 的影响。它们通过链式法则逐层向前回传,详细步骤如下:
1. 损失相对于第 l 层输出的导数:

2. 损失相对于权重的导数:
前向传播中线性组合的公式,可以看到,z(l) 是由 W(l)和 a(l−1) 相乘得到的。因此,z(l) 对 W(l) 的导数为:

通过链式法则计算损失函数对权重 W(l) 的导数:

得到结果:

这里,a{(l-1)}T 是上一层的激活值的转置,目的是确保矩阵的维度正确。由于 W(l) 是一个矩阵,通常 a(l−1) 是一个列向量,因此 a{(l-1)}T 是一个行向量。
3. 损失相对于偏置的导数:
在线性组合公式中,偏置 b(l) 是直接加到每个神经元的线性组合 z(l) 中的。因此,z(l) 对 b(l) 的导数是 1:

通过链式法则,我们可以计算损失函数 L 对偏置 b(l) 的导数:

所以:

4. 损失相对于第 l−1层线性组合 z(l−1)的导数:
根据线性组合的公式,z(l) 对 a(l−1) 的导数是权重矩阵 W(l):

通过链式法则,损失函数对上一层激活值 a(l−1) 的导数可以表示为损失函数对当前层线性组合 z(l) 的导数乘以 z(l) 对 a(l−1) 的导数:
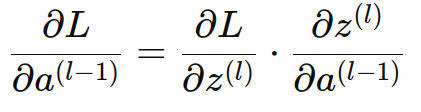
代入前面推导出的公式:

为了保持一致性,我们通常将 W(l) 转置,使得矩阵运算中的维度保持一致:
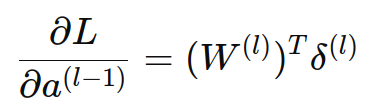
因为每一层的激活值 a(l−1) 是通过激活函数 g(z(l−1)) 得到的:

所以:

即:

⊙ 表示逐元素相乘(Hadamard 乘积),激活函数是逐元素应用到每个神经元输出的,而不是对整个向量进行操作。因此,第 l 层的每个神经元在反向传播时都会依赖于其对应的激活函数导数。
四、 权重和偏置更新(Weight and Bias Update)
使用梯度下降法,根据反向传播计算得到的梯度更新权重和偏置。
1. 权重更新公式:
对于第 l 层的权重 W(l),更新公式为:

其中:
- η 是学习率。
- ∂W(l)∂E=δ(l)(a(l−1))T 是损失函数对第 l 层权重的梯度。
2. 偏置更新公式:
类似地,第 l 层的偏置 b(l) 更新公式为:

五、 循环迭代
通过多次迭代(通常称为训练迭代(epochs)),重复进行前向传播、损失函数计算、反向传播以及权重和偏置的更新,直到网络收敛,即损失函数的值不再显著下降,或者达到了预设的迭代次数。
Rumelhart 对反向传播算法的贡献:
David Rumelhart 及其同事的主要贡献在于:
- 他们系统化地提出了反向传播算法,使得该算法可以有效应用于多层神经网络的训练,解决了之前单层感知器模型的局限性。
- 他们展示了如何通过反向传播算法训练深层网络,使得网络能够从数据中学习复杂的模式表示。这为后来的深度学习发展奠定了基础。
反向传播的意义与局限:
反向传播算法是现代深度学习的核心之一,它使得多层神经网络能够成功训练,解决了许多复杂的任务(如图像识别、语音识别等)。但是,它也有一些局限性,例如:
- 梯度消失问题(vanishing gradient):在深层神经网络中,反向传播的梯度逐渐减小,导致前几层权重更新非常缓慢。
- 训练时间长:当网络层数增加或数据集规模扩大时,训练时间可能会变得非常长。
尽管如此,反向传播算法依然是当今神经网络训练的基础,配合现代改进的优化方法(如Adam、RMSprop等)和技术(如Batch Normalization、Dropout等),反向传播已经极大地提升了神经网络的学习效率和表现。
