三次样条样条：Bézier样条和Hermite样条
总结 What is the Difference Between Natural Cubic Spline, Hermite Spline, Bézier Spline and B-spline?
1.多项式拟合中的 Runge Phenomenon
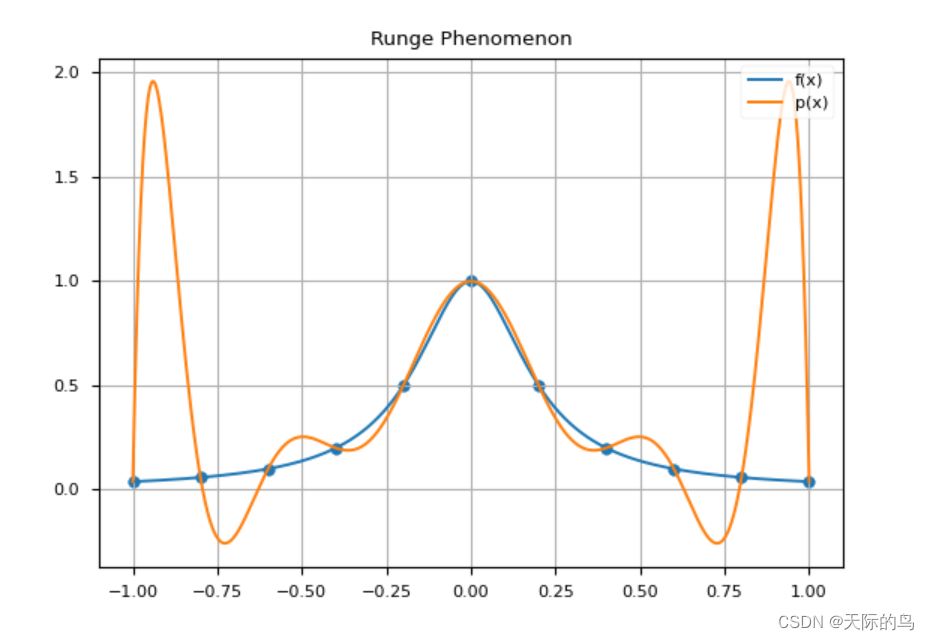
找到一条通过N+1个点的多项式曲线 ，需要N次曲线。通过两个点的多项式曲线为一次，三个点的多项式曲线为二次。当点数较多时，曲线阶数增高，在端点处易出现 Runge Phenomenon。这种现象是指，在曲线阶数较高时，拟合的结果可能在端点处与实际产生很大的误差。比如下图中，蓝色曲线是实际曲线，橙色是对11个点拟合产生得到10次多项式，在端点处发生了很大的抖动。
2.Bernstein Polynomials（伯恩斯坦多项式）and Bézier Curves（贝塞尔曲线）
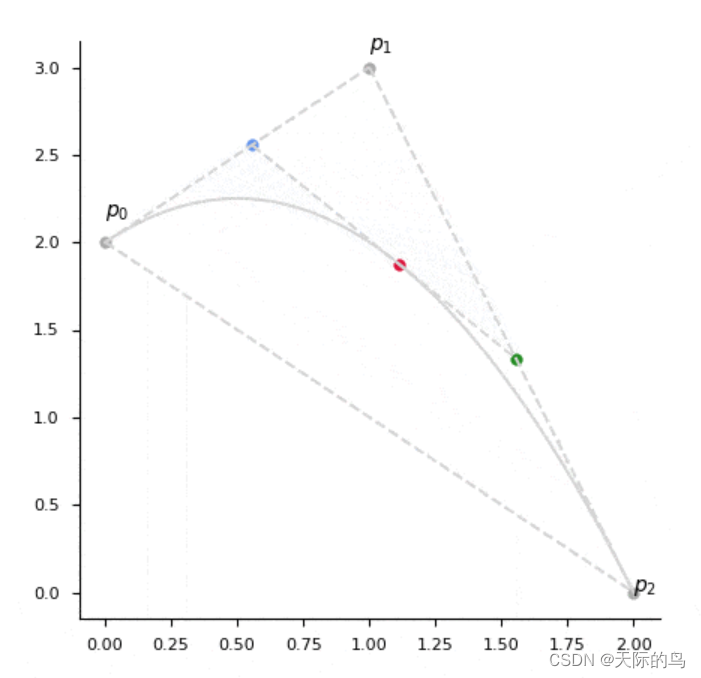
伯恩斯坦多项式的图解：下图中，黄蓝色点从P0往P1匀速前进，在0时刻位于P0，在1时刻位于P1；类似地绿色点从P1匀速朝着P2前进，那么蓝点和绿点就是一条位置和长度都动态变化的线段。在这个前提下，红色点沿着动态的蓝绿线段“匀速”前进，“匀速”的含义是蓝红线段长度除以蓝绿线段的长度的值，等于时间t，即这个值在0时刻等于0，在1时刻等于1。
根据上边的情况，可以推导出红点的位置与时间t的关系为下图。可以得出，红点的位置，是P0，P1，P2的一个组合。红点的位置曲线随着三个控制点P0P1P2的变化而唯一确定。
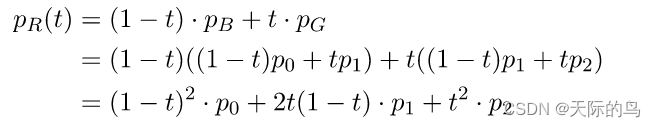
三个控制点前的系数叫做Bernstein basis polynomials，红点的位置曲线叫做二次贝塞尔曲线。可以注意到，二次贝塞尔曲线的三个控制点中，有两个在曲线上，作为曲线的起点和终点，一般是固定的。那么曲线就由第三个控制点唯一确定，在Bezier tool上通过拖动这个控制点，可以方便地获得自己想要的二次贝塞尔曲线。
伯恩斯坦二次多项式基底，注意这个基地是可以扩展到更高次的，详见bezier + spline。即对于三个控制点可以用二次贝萨尔曲线拟合，四个控制点可以用三次拟合，以此类推。高阶的贝萨尔曲线可能会比较复杂，使用分段贝萨尔曲线就可以得到B-样条。具体参考贝萨尔曲线和B样条
3.Hermite Basis Polynomials and Cubic Hermite Interpolation
Hermite曲线：考虑一个关于时间t的三次多项式 p(t) = at^3 + bt^2 + ct + d，他有四个未知数，那么找到找到四个等式，那么就能解析出四个未知数。首尾端点可以构造出两个等式，Hermite曲线假设首尾端点处的斜率也是已知的，那么就有四个不相关的条件构造出四个等式，唯一地解出多项式。
Hermite多项式的**四个条件**
解析出的Hermite三次多项式
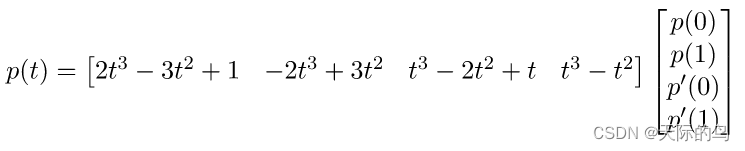
注意Hermite曲线与贝塞尔曲线有一个共同点 ：首尾端点固定的情况下，利用某些额外的条件，寻找一条平滑的曲线。
4.三次样条
样条函数是使用最多的分段多项式插值方法，k次样条由多段k次多项式曲线组成。一个k次样条，除了函数值连续，在曲线区间内，也是k-1次可微（k-2次导数连续），并且k-1次导数连续。使用最多的是三次样条，相较于一次和二次样条，它具有平滑和变化的二阶导数，具有更多的变换性质。
自然样条：得到的曲线通过所有的节点，一个控制点位置的改变，会影响其他段的曲线，是非local的
B-spline：得到的曲线是节点的加权平均，不保证通过节点，是一种拟合，能保证二阶导连续 。且优点是移动一个控制点，其他点不一定会变化
贝塞尔曲线：由控制点确定，通过起点和终点，能保证一阶导连续
分段Hermite：给定每一段曲线起点和终点的一阶导数，就可以确定曲线，可以控制一阶导数连续。
###6. 个人总结
三次样条：得到的曲线通过每一个节点，一阶导二阶导都连续，不过当一个节点发生变化时，整个曲线需要重新计算。
B-样条：把节点认为是控制点，曲线不一定经过节点，是一个近似的拟合。优点是，可以单独改变某一段曲线，而不影响其他段。