引言

上一节介绍了$\text{M-P}$神经元模型，并介绍了感知机算法$(\text{Perceptron})$的参数调整过程。本节将介绍多层前馈神经网络，并介绍反向传播算法。

回顾：感知机算法

关于感知机算法，它本质上是一个仅包含一个$\text{M-P}$神经元的神经网络模型。以基本逻辑运算与为例，它们对应感知机算法的网络模型表示如下：
需要注意的是，这里的$x_1,x_2$是输入层，它们均表示‘样本特征的随机变量’，因而它们仅是‘接收外部信号的载体’，并不是$\text{M-P}$神经元模型。

对应计算流程表示如下：
$${\mathcal{Y}}_{out}=f\left({\mathcal{W}}_1\cdot x_1+{\mathcal{W}}_2\cdot x_2-\theta \right)$$
对于上述计算流程中的权重${\mathcal{W}}_1,{\mathcal{W}}_2$和阈值$\theta$，可将阈值$\theta$视作一个固定输入的哑结点($\text{Dummy Node}$)与对应权重的线性组合，从而使学习过程可统一为权重的学习过程：
$${\mathcal{Y}}_{out}=f({\mathcal{W}}_1\cdot x_1+{\mathcal{W}}_2\cdot x_2+{\mathcal{W}}_{\text{Dum}}\cdot \underset{\text{Fixed}}{\underbrace{x_{\text{Dum}}}})$$
关于感知机算法权重学习过程的参数调整使用梯度下降法。针对逻辑计算与，本质上是二分类问题。感知机算法关于策略的构建动机是策略驱动：
$$\begin{array}{rl}& \{\begin{array}{l}{\mathcal{L}}_{\text{True}}(\mathcal{W})={\sum }_{(x^{(i)},y^{(i)})\in \mathcal{D}}{\hat{y}}^{(i)}\left({\mathcal{W}}^T{x}^{(i)}\right)\\ \underset{\mathcal{W}}{\mathrm{argmax}}{\mathcal{L}}_{\text{True}}(\mathcal{W})\end{array}\\ & \{\begin{array}{l}{\mathcal{L}}_{\text{False}}(\mathcal{W})=-{\sum }_{(x^{(i)},y^{(i)})\in \mathcal{D}}{y}^{(i)}\left({\mathcal{W}}^T{x}^{(i)}\right)\\ \underset{\mathcal{W}}{\mathrm{argmin}}{\mathcal{L}}_{\text{False}}(\mathcal{W})\end{array}\end{array}$$
关于感知机权重的调整过程可表示为：
$$\begin{array}{rl}{\mathcal{W}}^{(t+1)}& \Leftarrow {\mathcal{W}}^{(t)}-\eta \cdot {\nabla }_{\mathcal{W}}\mathcal{L}(\mathcal{W})\\ & ={\mathcal{W}}^{(t)}-\eta \cdot \left[\frac{\partial {\mathcal{L}}_{\text{False}}(\mathcal{W})}{\partial \mathcal{W}}+\frac{\partial {\mathcal{L}}_{\text{True}}(\mathcal{W})}{\partial \mathcal{W}}\right]\\ & ={\mathcal{W}}^{(t)}-\eta \cdot \sum _{(x^{(i)},y^{(i)})\in \mathcal{D}}\left({\hat{y}}^{(i)}-y^{(i)}\right)x^{(i)}\\ & ={\mathcal{W}}^{(t)}+\eta \cdot \sum _{(x^{(i)},y^{(i)})\in \mathcal{D}}\left(y^{(i)}-{\hat{y}}^{(i)}\right)x^{(i)}\end{array}$$

其中$\eta$表示学习率($\text{Learning Rate}$)。关于迭代结束的标志：当关于样本特征$x^{(i)}$的预测结果${\hat{y}}^{(i)}$与真实标签$y^{(i)}$相等，此时${\mathcal{W}}^{(t)}\Rightarrow {\mathcal{W}}^{(t+1)}$不会发生变化，迭代可以停止。

非线性问题与多层感知机

在前馈神经网络——非线性问题中已经对解决非线性问题的方式进行了介绍，这里不再赘述。这里仅从$\text{M-P}$神经元模型的角度重温一下处理亦或问题的多层感知机结构：

很明显，这是一个两层感知机，其中包含输入层结点$x_1,x_2$，输出层结点$\mathcal{Y}$以及隐含层($\text{Hidden Layer}$)结点$h_1,h_2$。

相比于感知机算法，上述多层感知机明显由$3$个$\text{M-P}$神经元模型嵌套组合的结构。并且神经元之间不存在同层连接，也不存在跨层连接。这种神经网络结构被称作多层前馈神经网络($\text{Multi-Layer Feed-Forward Neural Network}$)。
以上述结构为例，输入层不算网络层数，因而上述结构被称作‘两层网络’。但如果将隐藏层、输出层区分开，也可以将其称作：单隐层网络。

上述模型需要学习的权重参数有：
Θ={W11,W12,W21,W22,θ1,θ2,θ3}\Theta = \{\mathcal W_{11},\mathcal W_{12},\mathcal W_{21},\mathcal W_{22},\theta_1,\theta_2,\theta_3\}Θ={W11​,W12​,W21​,W22​,θ1​,θ2​,θ3​}

反向传播算法($\text{BackPropagation,BP}$)

虽然上述的神经网络结构能够处理非线性问题，但关于权重参数$\Theta$的学习过程，仅使用如错误驱动这种简单策略是不够的。
由于$\text{M-P}$神经元的嵌套，使得网络结构变得更加复杂，仅通过随机调整参数去观察$y^{(i)}-{\hat{y}}^{(i)}$的计算代价是极大的。

针对于多层神经网络，反向传播算法就是其中最杰出的代表。下面通过示例对梯度的反向传播过程进行描述。

场景构建

关于数据集合$\mathcal{D}$的描述表示如下：
这里为了泛化起见，并没有将标签$y^{(i)}(i=1,2,\cdots ,N)$约束为标量，而是一个包含$l$个随机变量的向量形式。
D={x(i),y(i)}i=1Nx(i)∈Rd;y(i)∈Rl\mathcal D = \{x^{(i)},y^{(i)}\}_{i=1}^N \quad x^{(i)} \in \mathbb R^{d};y^{(i)} \in \mathbb R^lD={x(i),y(i)}i=1N​x(i)∈Rd;y(i)∈Rl
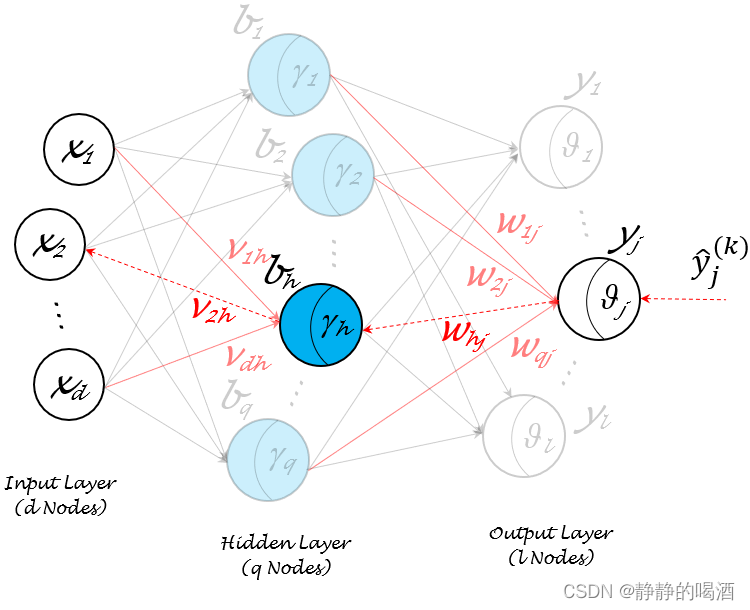
上述条件已经给出了输入层、输出层的规模分别是$d,l$，基于此构建一个含一个隐藏层的、隐藏层内神经元个数为$q$的单隐层前馈神经网络：

观察上图，除了输入层，隐藏层、输出层的结点均是$\text{M-P}$神经元模型：

• 其中隐藏层神经元的阈值分别表示为：{γ1,γ2,⋯,γq}\{\gamma_1,\gamma_2,\cdots,\gamma_q\}{γ1​,γ2​,⋯,γq​}；输出层神经元的阈值分别表示为：{θ1,θ2,⋯,θl}\{\theta_1,\theta_2,\cdots,\theta_l\}{θ1​,θ2​,⋯,θl​}；
• 输入层结点{x1,x2,⋯,xd}\{x_1,x_2,\cdots,x_d\}{x1​,x2​,⋯,xd​}指向隐藏层第$h$个神经元$b_h$的权重分别表示为：{v1h,v2h,⋯,vdh}\{v_{1h},v_{2h},\cdots,v_{dh}\}{v1h​,v2h​,⋯,vdh​}；同理，隐藏层神经元{b1,b2,⋯,bq}\{b_1,b_2,\cdots,b_q\}{b1​,b2​,⋯,bq​}指向输出层第$j$个神经元$y_j$的权重分别表示为：{w1j,w2j,⋯,wqj}\{w_{1j},w_{2j},\cdots,w_{qj}\}{w1j​,w2j​,⋯,wqj​}；
• 关于隐藏层神经元$b_h$接收到的输入${\alpha }_h$可表示为：
  $${\alpha }_h=v_{1h}\cdot x_1+\cdots +v_{dh}\cdot x_d=\sum _{i=1}^d{v}_{ih}\cdot x_i$$
• 关于输出层神经元$y_j$接收到的输入${\beta }_j$可表示为：
  $${\beta }_j=w_{1j}\cdot b_1+\cdots +w_{qj}\cdot b_q=\sum _{i=1}^q{w}_{ij}\cdot b_i$$

这里假设隐藏层、输出层神经元使用$\text{Sigmoid}$函数作为激活函数。并以回归任务为例，针对某一具体样本$(x^{(k)},y^{(k)})\in \mathcal{D}$进行计算。

求解各权重更新量

针对具体样本$(x^{(k)},y^{(k)})$，将样本特征$x^{(k)}=(x_1^{(k)},x_2^{(k)},\cdots ,x_d^{(k)}{)}^T$带入到神经网络中，从$\text{M-P}$神经元的角度观察，对应神经网络的输出${\hat{y}}^{(k)}=({\hat{y}}_1^{(k)},{\hat{y}}_2^{(k)},\cdots ,{\hat{y}}_l^{(k)}{)}^T$表示为：

• 这里实际上描述的并不准确，因为${\beta }_j,{\theta }_j$仅表示泛化的样本$x$作为输入层的输入，对应的接收结果和阈值。如果针对真实样本$(x^{(k)},y^{(k)})$,应该写作${\beta }_j^{(k)},{\theta }_j^{(k)}$，这里为了节约符号，直接用${\beta }_j,{\theta }_j$替代。
• 这里仅描述了神经元$y_j$的输出信息。
  $${\hat{y}}_j^{(k)}=f({\beta }_j-{\theta }_j)=f\left(\sum _{i=1}^q{w}_{ij}\cdot b_i-{\theta }_j\right)j=1,2,\cdots ,l$$

由于是回归任务，因而这里使用 均方误差($\text{Mean-Square Error,MSE}$)来描述神经网络输出${\hat{y}}^{(k)}$与真实标签$y^{(k)}$之间的误差关系。关于$(x^{(k)},y^{(k)})$的误差结果${\mathcal{E}}^{(k)}$表示如下：

• 这里由于只有$1$个样本，均值部分$\frac{1}{1}$就直接省略掉了。
• 系数$\frac{1}{2}$仅是为后续求导便利使用。对其求解梯度过程中，仅改变梯度大小，梯度方向不会发生变化。
  $$\begin{array}{rl}{\mathcal{E}}^{(k)}& =\frac{1}{2}(y^{(k)}-{\hat{y}}^{(k)}{)}^2\\ & =\frac{1}{2}\sum _{j=1}^l(y_j^{(k)}-{\hat{y}}_j^{(k)}{)}^2\end{array}$$

重新观察${\hat{y}}^{(k)}$，想通过上述神经网络得到一个具体预测结果，需要学习的权重有：
这里说的权重，包含阈值。

• 输入层与隐藏层之间所有连接的权重信息：一共$q\times d$个；
• 隐藏层与输出层之间所有连接的权重信息：一共$q\times l$个；
• 隐藏层自身的阈值数量：$q$个；
• 输出层自身的阈值数量：$l$个；

总共包含$(d+l+1)\times q+l$个权重需要学习。这里以输出层某神经元$y_j$与隐藏层某神经元$b_h$之间的连接权重${\mathcal{W}}_{h_j}$为例，计算该权重的更新量：
需要注意的是，该操作仅仅是梯度下降的操作，而不是反向传播算法。
$$\{\begin{array}{l}{\mathcal{W}}_{hj}^{(t+1)}={\mathcal{W}}_{hj}^{(t)}+△{\mathcal{W}}_{hj}^{(t)}\\ △{\mathcal{W}}_{hj}^{(t)}=-\eta \cdot \frac{\partial {\mathcal{E}}^{(k)}}{\partial {\mathcal{W}}_{hj}^{(t)}}\end{array}$$

观察上图，${\mathcal{W}}_{hj}$首先影响的是输出层的第$j$个$\text{M-P}$神经元$y_j$，基于神经元$y_j$接收到的输入是${\beta }_j$，对应输出特征是${\hat{y}}_j^{(k)}$。使用链式求导法则，将$\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\mathcal{W}}_{hj}^{(t)}}$表示为如下形式：
$$\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\mathcal{W}}_{hj}^{(t)}}=\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\hat{y}}_j^{(k)}}\cdot \frac{\partial {\hat{y}}_j^{(k)}}{\partial {\beta }_j}\cdot \frac{\partial {\beta }_j}{\partial {\mathcal{W}}_{hj}^{(t)}}$$
插一句，由于激活函数是$\text{Sigmoid}$函数，关于它的导数可以表示为如下形式：
$$\begin{array}{rl}{f}^{\prime }(x)& ={\left[\frac{1}{1+e^{-x}}\right]}^{\prime }\\ & =\frac{1+e^{-x}-1}{{\left[1+e^{-x}\right]}^2}\\ & =\frac{1}{1+e^{-x}}\cdot \left[1-\frac{1}{1+e^{-x}}\right]\\ & =f(x)\cdot [1-f(x)]\end{array}$$
因而关于链式求导法则中的各项表示如下：

• 第一项$\begin{array}{r}\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\hat{y}}_j^{(k)}}\end{array}$：
  将不含${\hat{y}}_j^{(k)}$的项，视作常数。
  $$\begin{array}{rl}\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\hat{y}}_j^{(k)}}& =\frac{\partial }{\partial {\hat{y}}_j^{(k)}}\left[\frac{1}{2}\sum _{j=1}^l{\left(y_j^{(k)}-{\hat{y}}_j^{(k)}\right)}^2\right]\\ & =\frac{\partial }{\partial {\hat{y}}_j^{(k)}}\left\{\frac{1}{2}\left[\underset{=0}{\underbrace{\sum _{\ne j}^l{\left(y_j^{(k)}-{\hat{y}}_j^{(k)}\right)}^2}}+{\left(y_j^{(k)}-{\hat{y}}_j^{(k)}\right)}^2\right]\right\}\\ & =\frac{\partial }{\partial {\hat{y}}_j^{(k)}}\left[\frac{1}{2}{\left(y_j^{(k)}-{\hat{y}}_j^{(k)}\right)}^2\right]\\ & =-(y_j^{(k)}-{\hat{y}}_j^{(k)})\end{array}$$
• 第二项$\begin{array}{r}\frac{\partial {\hat{y}}_j^{(k)}}{\partial {\beta }_j}\end{array}$：
  需要注意的点，不要将阈值忘掉，并且${\hat{y}}_j^{(k)}=\text{Sigmoid}({\beta }_j-{\theta }_j)$
  $$\begin{array}{rl}\frac{\partial {\hat{y}}_j^{(k)}}{\partial {\beta }_j}& =\frac{\partial }{\partial {\beta }_j}\left[\text{Sigmoid}({\beta }_j-{\theta }_j)\right]\\ & ={\hat{y}}_j^{(k)}\cdot \left[1-{\hat{y}}_j^{(k)}\right]\end{array}$$
• 第三项$\begin{array}{r}\frac{\partial {\beta }_j}{\partial {\mathcal{W}}_{hj}}\end{array}$。根据${\beta }_j$与${\mathcal{W}}_{hj}$之间的关系：
  其中只有一项${\mathcal{W}}_{hj}\cdot b_h$和${\mathcal{W}}_{hj}$相关.
  $$\begin{array}{rl}{\beta }_j& =\sum _{i=1}^q{\mathcal{W}}_{ij}\cdot b_i\\ & ={\mathcal{W}}_{1j}\cdot b_1+\cdots +{\mathcal{W}}_{hj}\cdot b_h+\cdots +{\mathcal{W}}_{qj}\cdot b_q\end{array}$$
  因而有：
  $$\begin{array}{r}\frac{\partial {\beta }_j}{\partial {\mathcal{W}}_{hj}}=b_h\end{array}$$

至此，关于${\mathcal{W}}_{hj}$的更新量$△{\mathcal{W}}_{hj}$可表示为：
$$\begin{array}{rl}△{\mathcal{W}}_{hj}& =-\eta \cdot \frac{\partial {\mathcal{E}}^{(k)}}{\partial {\mathcal{W}}_{hj}}\\ & =-\eta \cdot \frac{\partial {\mathcal{E}}^{(k)}}{\partial {\hat{y}}_j^{(k)}}\cdot \frac{\partial {\hat{y}}_j^{(k)}}{\partial {\beta }_j}\cdot \frac{\partial {\beta }_j}{\partial {\mathcal{W}}_{hj}^{(t)}}\\ & =-\eta \cdot \left[-(y_j^{(k)}-{\hat{y}}_j^{(k)})\right]\cdot {\hat{y}}_j^{(k)}\cdot \left[1-{\hat{y}}_j^{(k)}\right]\cdot b_h\\ & =\eta \cdot {\hat{y}}_j^{(k)}\cdot (1-{\hat{y}}_j^{(k)})\cdot (y_j^{(k)}-{\hat{y}}_j^{(k)})\cdot b_h\end{array}$$
同理，其他权重更新量$△{\theta }_j,△{\gamma }_h,△v_{ih}^{(k)}$的求解过程分别表示为：

• ${\theta }_j$的权重更新量$△{\theta }_j$：
  ${\theta }_j$和$△{\mathcal{W}}_{hj}$仅相差一个$-b_h$项.
  $$\begin{array}{rl}△{\theta }_j& =-\eta \cdot \frac{\partial {\mathcal{E}}^{(k)}}{\partial {\theta }_j}\\ & =-\eta \cdot \frac{\partial {\mathcal{E}}^{(k)}}{\partial {\hat{y}}_j^{(k)}}\cdot \frac{\partial {\hat{y}}_j^{(k)}}{\partial {\theta }_j}\\ & =-\eta \cdot \left[-(y_j^{(k)}-{\hat{y}}_j^{(k)})\right]\cdot {\hat{y}}_j^{(k)}\cdot \left(1-{\hat{y}}_j^{(k)}\right)\cdot (0-1)\\ & =-\eta \cdot {\hat{y}}_j^{(k)}\cdot (1-{\hat{y}}_j^{(k)})\cdot (y_j^{(k)}-{\hat{y}}_j^{(k)})\end{array}$$
• ${\gamma }_h$的权重更新量$△{\gamma }_h$：
  其中$b_h^{(k)}$表示隐藏层的输出,其与${\alpha }_h,{\gamma }_h$之间的关系如下：
  $$\begin{array}{rl}{b}_h^{(k)}& =\text{Sigmoid}({\alpha }_h-{\gamma }_h)\\ & =\text{Sigmoid}\left(\sum _{i=1}^d{v}_{ih}^{(k)}\cdot x_i^{(k)}\right)\end{array}$$
  同上，关于隐藏层第$h$个神经元的阈值${\gamma }_h$具体是指${\gamma }_h^{(k)}$,这里为简化符号，不做修改.
  并且隐藏层神经元输出$b_h$与输出层的所有神经元之间均存在关联关系，因此需要加上${\sum }_{j=1}^l$.
  $$\begin{array}{rl}△{\gamma }_h& =-\eta \cdot \frac{\partial {\mathcal{E}}^{(k)}}{\partial {\gamma }_h}\\ & =-\eta \cdot \frac{\partial {\mathcal{E}}^{(k)}}{\partial b_h^{(k)}}\cdot \frac{\partial b_h^{(k)}}{\partial {\gamma }_h}\\ & =-\eta \cdot \sum _{j=1}^l\left(\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\hat{y}}_j^{(k)}}\cdot \frac{\partial {\hat{y}}_j^{(k)}}{\partial {\beta }_j}\cdot \frac{\partial {\beta }_j}{\partial b_h^{(k)}}\right)\cdot \frac{\partial b_h^{(k)}}{\partial {\gamma }_h}\\ & =-\eta \cdot \sum _{j=1}^l{\hat{y}}_j^{(k)}\cdot \left(1-{\hat{y}}_j^{(k)}\right)\cdot \left[-(y_j^{(k)}-{\hat{y}}_j^{(k)})\right]\cdot {\mathcal{W}}_{hj}\cdot \left[-b_h\cdot (1-b_h)\right]\\ & =-\eta \cdot [b_h\cdot (1-b_h)]\cdot \sum _{j=1}^l\left[{\mathcal{W}}_{hj}\cdot {\hat{y}}_j^{(k)}\cdot (1-{\hat{y}}_j^{(k)})\cdot (y_j^{(k)}-{\hat{y}}_j^{(k)})\right]\end{array}$$
• $v_{ih}^{(k)}$的权重更新量$△v_{ih}^{(k)}$：
  需要注意的点：$\begin{array}{r}\frac{\partial b_h^{(k)}}{\partial {\alpha }_h}\end{array}$与$\begin{array}{r}\frac{\partial b_h^{(k)}}{\partial {\gamma }_h}\end{array}$都是$\text{Sigmoid}$函数的导数，只不过差一个负号;$\begin{array}{r}\frac{\partial {\hat{y}}_j^{(k)}}{\partial {\beta }_j}\end{array}$和$\begin{array}{r}\frac{\partial {\hat{y}}_j^{(k)}}{\partial {\theta }_j}\end{array}$也是如此。
  $$\begin{array}{rl}△v_{ih}^{(k)}& =-\eta \cdot \frac{\partial {\mathcal{E}}^{(k)}}{\partial v_{ih}^{(k)}}\\ & =-\eta \cdot \frac{\partial {\mathcal{E}}^{(k)}}{\partial {\alpha }_h}\cdot \frac{\partial {\alpha }_h}{\partial v_{ih}^{(k)}}\\ & =-\eta \cdot \sum _{j=1}^l\left(\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\hat{y}}_j^{(k)}}\cdot \frac{\partial {\hat{y}}_j^{(k)}}{\partial {\beta }_j}\cdot \frac{\partial {\beta }_j}{\partial b_h^{(k)}}\cdot \frac{\partial b_h^{(k)}}{\partial {\alpha }_h}\right)\cdot \frac{\partial {\alpha }_h}{\partial v_{ih}^{(k)}}\\ & =\eta \cdot [b_h\cdot (1-b_h)]\cdot \sum _{j=1}^l\left[{\mathcal{W}}_{hj}\cdot {\hat{y}}_j^{(k)}\cdot (1-{\hat{y}}_j^{(k)})\cdot (y_j^{(k)}-{\hat{y}}_j^{(k)})\right]\cdot x_i^{(k)}\end{array}$$

图示描述反向传播过程

假设第$t$次迭代隐藏层神经元$b_h$、输出层神经元$y_j$的正向执行过程表示如下：
依然以某一具体样本$(x^{(k)},y^{(k)})\in \mathcal{D}$，并以预测结果的第$j$个分量$y_j^{(k)}$的反向传播作为示例进行描述.
$$\begin{array}{r}\{\begin{array}{l}{\alpha }_h={\sum }_{i=1}^d{v}_{ih}^{(k)}\cdot x_i^{(k)}\\ b_h^{(k)}=\text{Sigmoid}({\alpha }_h-{\gamma }_h)\\ {\beta }_j={\sum }_{h=1}^q{\mathcal{W}}_{hj}\cdot b_h\\ {\hat{y}}_j^{(k)}=\text{Sigmoid}({\beta }_j-{\theta }_j)\end{array}\end{array}$$

• 首先，针对预测结果${\hat{y}}_j^{(k)}$和真实标签$y_j^{(k)}$之间的误差结果对${\hat{y}}_j^{(k)}$的梯度$\begin{array}{r}\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\hat{y}}_j^{(k)}}\end{array}$进行计算：
  
• 梯度$\begin{array}{r}\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\hat{y}}_j^{(k)}}\end{array}$计算完成后，神经元$y_j$获取相应梯度，将该梯度传递给阈值${\theta }_j$以及各隐藏层神经元与$y_j$的连接权重$\begin{array}{r}\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\theta }_j},\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\mathcal{W}}_{hj}^{(k)}}\end{array}$：
  这里以隐藏层神经元$b_h$为关注点描述反向传播过程，因而仅点亮一条连接权重${\mathcal{W}}_{hj}$;但实际上与$y_j$相关联的权重均被点亮。
  
• 传递到神经元$b_h$后，首先对该神经元的预测结果$b_h^{(k)}$求解梯度；紧接着对神经元的阈值${\gamma }_h$和连接权重${\alpha }_h$求解梯度$\begin{array}{r}\frac{\partial {\mathcal{E}}^{(k)}}{\partial b_h^{(k)}},\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\gamma }_h},\frac{\partial {\mathcal{E}}^{(k)}}{\partial {\alpha }_h}\end{array}$：
  
  最终，当梯度传递至${\alpha }_h$后，对输入层与隐藏层的连接权重求解梯度$\begin{array}{r}\frac{\partial {\mathcal{E}}^{(k)}}{\partial v_{ih}^{(k)}}\end{array}$：
  这里以$i=2$为例，实际上所有与神经元$b_h$相关联的权重均被点亮。
  
  至此，经过上述过程后，所有神经元结点以及相关权重，均更新了梯度。而且该示例中每个隐藏层的神经元结点每次计算过程中均更新了$l$次权重，这与下一层结点(这里是指输出层结点)数量相关。

下一次迭代($t+1$)使用更新后的权重参数进行正向传播过程。

总结

总观反向传播算法，实际上就是一个链式求导法则的工具：

• 它自身没有具体的目标函数/策略，这里的目标函数是均方误差${\mathcal{E}}^{(k)}(k=1,2,\cdots ,N)$提供的；
• 它自身也不属于算法，这里的算法(更新量的作用，使用学习率$\eta$)是梯度下降法；

因此，反向传播算法是将传播过程的更新量计算出来，其余操作并未参与。因而，它并不算是真正意义上的算法，它的迭代次数是人为决定的；它自身也不存在收敛性。

相关参考：
机器学习(周志华著)