23.3.26总结
康托展开
是一个全排列与自然数的映射关系,康托展开的实质是计算当前序列在所有从小到大的全排列中的顺序,跟其逆序数有关。
例如:对于 1,2,3,4,5 来说,它的康托展开值为 0*4!+0*3!+0*2!+0*1!
对于 4,3,1,5,2 来说:
3 * 4!+2 * 3!+0 * 2!+1 * 1!+0 * 0!=85
c++中加快读入:
ios_base::sync_with_stdio(0);cin.tie(0); cout.tie(0);//加快读入
红黑树:
是一种高效的查找树,可以在 O(logN)时间内完成查找,增加和删除。
红黑树的平衡过程跟魔方复原非常像,大致过程就是:遇到什么样的节点排布,我们就对应怎么去调整。
1.节点是红色或黑色,根是黑色
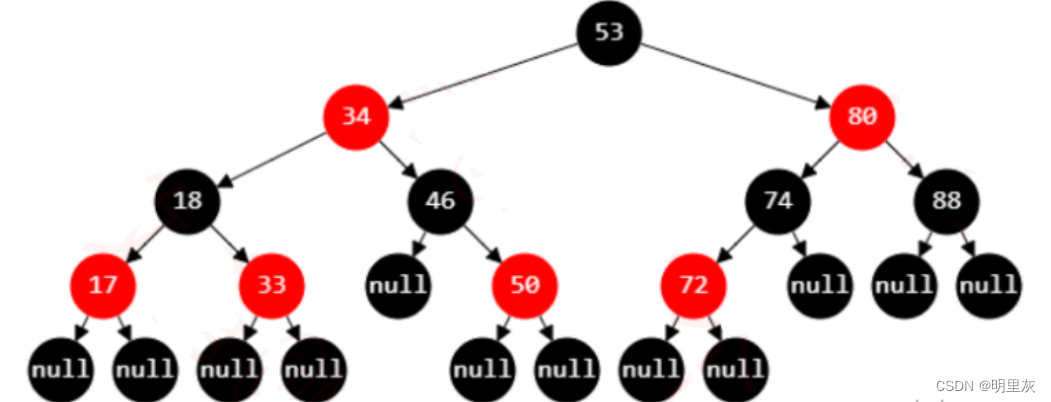
2.叶子节点(外部节点,空节点)都是黑色,这里的叶子节点指的是最底层的空节点(外部节点),下图中的那些null节点才是叶子节点,叶子节点不存储数据,null 节点的父节点在红黑树里不将其看作叶子节点
2.红色节点的子节点都是黑色,红色节点的父节点都是黑色
3.从根节点到叶子节点的所有路径上不能有 2 个连续的红色节点
5.从任一节点到叶子节点的所有路径都包含相同数目的黑色节点
简单搜索&&进阶搜索 - Virtual Judge (vjudge.net)
http://t.csdn.cn/xmPLc
简单搜索&&进阶搜索 - Virtual Judge (vjudge.net)
http://t.csdn.cn/zMf4v
cf补题:
Problem - G2 - Codeforces
http://t.csdn.cn/hWQx5
