当前位置： 首页 > news >正文

吴恩达机器学习课后题-01线性回归

news 2025/8/3 5:37:42

线性回归

  • 一.单变量线性回归
    • 题目
    • 损失函数（代价函数）
    • 梯度下降函数
    • 代价函数可视化
    • 整体代码
  • 二.多变量线性回归
    • 特征归一化（特征缩放）
    • 不同学习率比较
  • 正规方程
    • 正规方程与梯度下降比较
  • 使用列表创建一维数组
  • 使用嵌套列表创建二维数组（矩阵）
  • 创建一个3x3的零矩阵
  • 创建一个3x3的1矩阵
  • 创建一个3x3的矩阵，所有元素都是42
  • 使用arange生成一个一维数组
  • 使用linspace在指定间隔内生成均匀间隔的数值
  • 生成一个3x3的随机浮点数矩阵
  • 生成一个3x3的随机整数矩阵，元素范围在0到10之间

一.单变量线性回归

题目

在这里插入图片描述

numpy:科学计算库，处理多维数组，进行数据分析
pandas :是基于NumPy的一种工具，该工具是为了解决数据分析任务而创建的
Matplotlib:Python 的2D绘图库
matplotlib.pyplot:提供一个类似matlab的绘图框架

在这里插入图片描述
在这里插入图片描述
dataframe转数组三种方式
dataframe - > ndarray.
1.df.xalues,
2.df.as_matrix()
3.np.array(df)

绘制散点图
在这里插入图片描述

import numpy as np
import pandas as pd
import matplotlib.pyplot as pltdata=pd.read_csv("E:/学习/研究生阶段/python-learning/吴恩达机器学习课后作业/code/ex1-linear regression/ex1data1.txt",names=["population","profit"])
#print(data.describe())
data.plot.scatter("population","profit",label="population")
plt.show()

损失函数（代价函数）

在这里插入图片描述

def costfunction(x,y,theta):inner=np.power ( x @ theta-y,2)return np.sum(inner)/(2*len(x))

这个函数 costfunction 是用来计算线性回归中的成本（或损失）函数的，具体来说是均方误差（Mean Squared Error, MSE）成本函数。这个函数接受三个参数：x（特征矩阵），y（目标变量向量），和theta（参数向量，即线性模型的权重和偏置项）。下面是该函数的详细解释：

参数解释：
x：特征矩阵，其形状通常为 (m, n)，其中 m 是样本数量，n 是特征数量（不包括偏置项）。
y：目标变量向量，其形状为 (m,)，即每个样本对应一个目标值。
theta：参数向量，其长度应与 x 的特征数量加1相等（如果 x 不包含偏置项的话），因为我们需要一个额外的偏置项。theta 的第一个元素通常被认为是偏置项（截距），而其余元素对应于每个特征的权重。
函数逻辑：
x @ theta：这是矩阵乘法操作，计算 x 和 theta 的点积。如果 theta 的第一个元素是偏置项，那么 x 应该包含一列全为1的列（通常作为第一列），以对应偏置项。这样，x @ theta 的结果就是一个预测值向量，其形状与 y 相同（(m,)）。
np.power(x @ theta - y, 2)：计算预测值与实际值之间的差的平方。这是计算误差的一种方式，平方是为了确保所有误差都是正的，并且能够放大较大的误差。
np.sum(inner)：将上一步得到的误差平方向量中的所有元素相加，得到总误差。
return np.sum(inner)/(2len(x))：将总误差除以 2m（其中 m 是样本数量），得到平均误差的平方的一半。除以2主要是为了在求导时简化表达式，因为在实际应用中，我们经常需要计算成本函数的梯度，而这个操作可以简化梯度的计算。
注意事项：
在使用这个函数之前，需要确保 x 包含了偏置项（即一列全为1的列），除非你的 theta 已经被相应地调整过（例如，theta 的第一个元素不代表偏置项）。
确保 np（NumPy库）已经被正确导入，因为函数中用到了 np.power 和 np.sum 等NumPy库中的函数。
这个函数是线性回归模型训练过程中的一个重要组成部分，通过最小化这个成本函数，我们可以找到最佳的 theta 值，使得模型的预测值尽可能接近实际值。

[[0.]  [0.]]

这个数据是一个二维的浮点数列表（或可以视为一个2x1的矩阵），用Python的列表表示法来表示。每个子列表都包含一个浮点数 0.，表示0.0（即0的浮点数表示）。具体来说，数据是这样的：

python
[
[0.], # 第一个子列表，包含一个浮点数0.0
[0.] # 第二个子列表，也包含一个浮点数0.0
]
在Python中，这种数据结构是一个嵌套的列表（list of lists），外层列表包含两个元素，每个元素都是一个包含一个浮点数的内层列表。这种数据结构可以很方便地用numpy库转换成矩阵（numpy array）进行处理。

例如，使用numpy可以这样转换：

python
import numpy as np

data = [[0.], [0.]]
matrix = np.array(data)
print(matrix)
这段代码会输出：

[[0.]
[0.]]
这就是一个2x1的浮点数矩阵。在数据分析、机器学习或科学计算中，这种数据结构非常常见，特别是当使用numpy、pandas或其他科学计算库时。

梯度下降函数

"""
定义梯度下降函数
alpha:学习速率
inters:迭代次数
"""
def gradientDescent(x,y,theta,alpha,inters):for i in range(inters):costs=[]theta=theta-(x.T @ (x@theta-y))*alpha/len(x)cost=costfunction(x,y,theta)costs.append(cost)if i%100==0:print(cost)return theta,costs

代价函数可视化

在这里插入图片描述
fig是整张图
ax是

import numpy as np
import pandas as pd
import matplotlib.pyplot as pltfig, ax =plt.subplots()
ax.plot()
plt.show()

在这里插入图片描述
在这里插入图片描述

import numpy as np
import pandas as pd
import matplotlib.pyplot as pltfig, ax =plt.subplots(2,2)
ax1=ax[0,1]
ax1.plot()
plt.show()

整体代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt#定义代价函数
def costfunction(x,y,theta):inner=np.power ( x @ theta-y,2)return np.sum(inner)/(2*len(x))"""
定义梯度下降函数
alpha:学习速率
inters:迭代次数
"""
def gradientDescent(x,y,theta,alpha,inters):costs=[]for i in range(inters):theta=theta-(x.T @ (x@theta-y))*alpha/len(x)cost=costfunction(x,y,theta)costs.append(cost)# if i%100==0:#     print(cost)return theta,coststheta=np.zeros((2,1))#theta初始值2x1零矩阵
alpha=0.02#学习速率初始化
inters=2000#迭代次数初始化
data=pd.read_csv("E:/学习/研究生阶段/python-learning/吴恩达机器学习课后作业/code/ex1-linear regression/ex1data1.txt",names=["population","profit"])
#print(data.describe())
#data.plot.scatter("population","profit",label="population")
#plt.show()
data.insert(0,"ones",1)
x=data.iloc[:,0:-1]#取数据的0-倒数第二列，取所有行
#print(x)
y=data.iloc[:,-1:]
x=x.valuesy=y.values#y.shape,求矩阵大小
theta,costs=gradientDescent(x,y,theta,alpha,inters)fig,ax=plt.subplots(1,2)
ax1=ax[0]
ax1.plot(np.arange(inters),costs)
ax1.set(xlabel="inters",ylabel="costs",title="costs Vs inters")x_=np.linspace(y.min(),y.max(),100)
print(x_)
y_=theta[0,0]+theta[1,0]*x_
ax2=ax[1]
ax2.scatter(x[:,1],y,label="training data")
ax2.plot(x_,y_,"r",label="predect")
ax2.legend()
plt.show()

在这里插入图片描述

二.多变量线性回归

在这里插入图片描述

特征归一化（特征缩放）

1. 消除特征值之间的量纲影响,各特征值处于同一数量级提升
2. 模型的收敛速度
3. 提升模型的精度

在我们面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛。

在这里插入图片描述

不同学习率比较

#多变量线性回归
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt#定义代价函数
def costfunction(x,y,theta):inner=np.power ( x @ theta-y,2)return np.sum(inner)/(2*len(x))"""
定义梯度下降函数
alpha:学习速率
inters:迭代次数
"""
def gradientDescent(x,y,theta,alpha,inters):costs=[]for i in range(inters):theta=theta-(x.T @ (x@theta-y))*alpha/len(x)cost=costfunction(x,y,theta)costs.append(cost)# if i%100==0:#     print(cost)return theta,coststheta=np.zeros((3,1))#theta初始值2x1零矩阵
alpha=[0.0003,0.003,0.03,0.3,0.0001,0.001,0.1]#学习速率初始化
inters=2000#迭代次数初始化"""
归一化函数
data.mean平均值
data.std标准差
"""
def normalize_feature(data):return (data-data.mean())/data.std()
data=pd.read_csv("E:/学习/研究生阶段/python-learning/吴恩达机器学习课后作业/code/ex1-linear regression/ex1data2.txt",names=["size","bedrooms","price"])
data=normalize_feature(data)
# data.plot.scatter("size","price",label="price")
# plt.show()
data.insert(0,"ones",1)
x=data.iloc[:,0:-1]#取数据的0-倒数第二列，取所有行
y=data.iloc[:,-1:]
x=x.values#datafram转数组格式
y=y.values#y.shape,求矩阵大小
fig,ax1=plt.subplots()
for _alpha in alpha:_theta, costs = gradientDescent(x, y, theta, _alpha, inters)ax1.plot(np.arange(inters),costs,label=_alpha)
ax1.legend()#显示图例标签
ax1.set(xlabel="inters",ylabel="costs",title="costs Vs inters")
plt.show()

在这里插入图片描述

正规方程

在这里插入图片描述

正规方程与梯度下降比较

在这里插入图片描述

"""
单变量线性回归为例
"""
import numpy as npimport pandas as pd
import matplotlib.pyplot as plt
#定义正规方程
def normalequation(x,y):theta = np.linalg.inv(x.T @ x) @ x.T @ yreturn thetadata=pd.read_csv("E:/学习/研究生阶段/python-learning/吴恩达机器学习课后作业/code/ex1-linear regression/ex1data1.txt",names=["population","profit"])
#print(data.describe())
#data.plot.scatter("population","profit",label="population")
#plt.show()
data.insert(0,"ones",1)
x=data.iloc[:,0:-1]#取数据的0-倒数第二列，取所有行
#print(x)
y=data.iloc[:,-1:]
x=x.values
y=y.values
theta=normalequation(x,y)
print(theta)
#线性回归求得的参数
theta1=np.array([[-3.8928815],[1.19274237]])
print(theta1)
print(type(theta),type(theta1))
fig,ax=plt.subplots()
x_=np.linspace(y.min(),y.max(),100)
# print(x_)
y_1=theta1[0,0]+theta1[1,0]*x_
y_2=theta[0,0]+theta[1,0]*x_
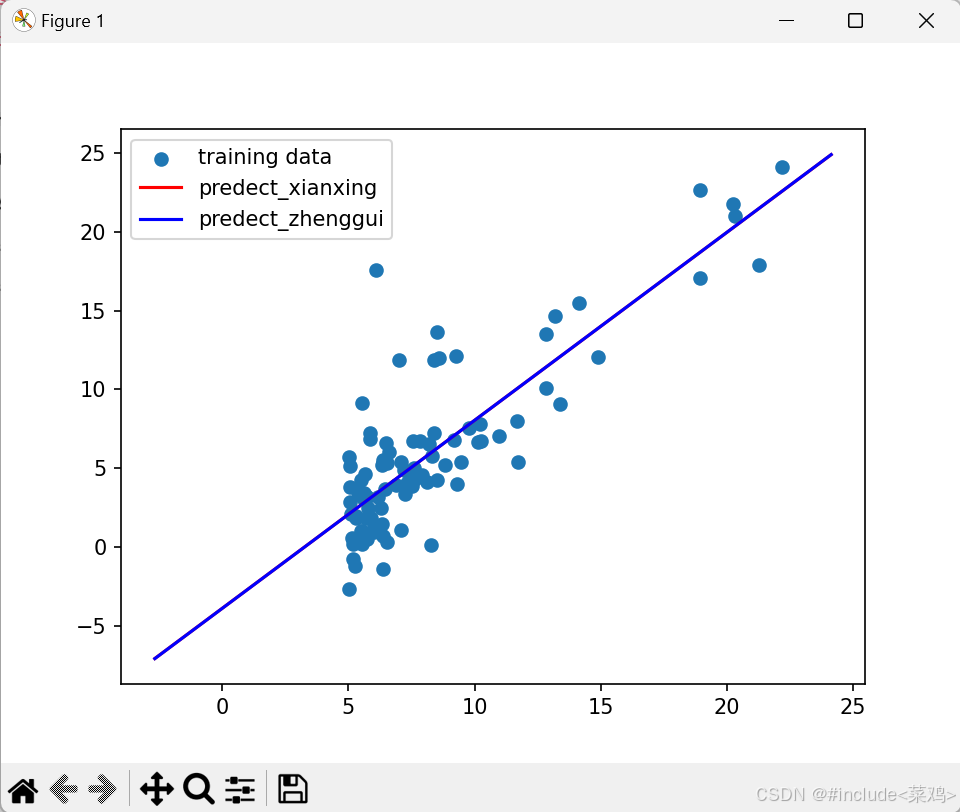
ax.scatter(x[:,1],y,label="training data")
ax.plot(x_,y_1,"r",label="predect_xianxing")
ax.plot(x_,y_2,"b",label="predect_zhenggui")
ax.legend()
plt.show()

结果
线性回归：theta1=[[-3.8928815],[1.19274237]]
正规方程：theta=[[-3.89578088]， [ 1.19303364]]
基本差不多
在这里插入图片描述

在Python中，numpy.ndarray是NumPy库提供的一个用于存储和操作大型多维数组和矩阵的核心对象。NumPy是Python的一个库，它提供了大量的数学函数工具，特别是针对数组的操作。要定义一个numpy.ndarray类型的矩阵，你首先需要安装并导入NumPy库，然后使用NumPy提供的函数或方法来创建数组。

以下是一些创建numpy.ndarray类型矩阵的基本方法：

  1. 使用numpy.array()
    这是最直接的方法，你可以将Python的列表（list）或其他序列类型转换为NumPy数组。

python
import numpy as np

使用列表创建一维数组

arr_1d = np.array([1, 2, 3, 4, 5])

使用嵌套列表创建二维数组（矩阵）

arr_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

print(arr_1d)
print(arr_2d)
2. 使用numpy.zeros(), numpy.ones(), numpy.full()
这些函数分别用于创建指定形状和类型，但所有元素分别为0、1或指定值的数组。

python

创建一个3x3的零矩阵

zero_matrix = np.zeros((3, 3))

创建一个3x3的1矩阵

ones_matrix = np.ones((3, 3))

创建一个3x3的矩阵，所有元素都是42

full_matrix = np.full((3, 3), 42)

print(zero_matrix)
print(ones_matrix)
print(full_matrix)
3. 使用numpy.arange(), numpy.linspace()
这些函数用于生成具有特定间隔的数值数组。

python

使用arange生成一个一维数组

arr_arange = np.arange(0, 10, 2) # 从0开始到10（不包括10），步长为2

使用linspace在指定间隔内生成均匀间隔的数值

arr_linspace = np.linspace(0, 10, 5) # 从0到10生成5个均匀间隔的数

print(arr_arange)
print(arr_linspace.reshape((2, -1))) # 将其重塑为2x2矩阵（注意：这里5个元素不能完美重塑为2x2，仅为示例）
4. 使用numpy.random模块
NumPy的random模块提供了多种生成随机数组的函数。

python

生成一个3x3的随机浮点数矩阵

random_matrix = np.random.rand(3, 3)

生成一个3x3的随机整数矩阵，元素范围在0到10之间

random_int_matrix = np.random.randint(0, 11, size=(3, 3))

print(random_matrix)
print(random_int_matrix)
以上就是在Python中使用NumPy库定义numpy.ndarray类型矩阵的几种基本方法。NumPy提供了丰富的函数和特性，使得数组和矩阵的操作变得既高效又方便。

http://www.lryc.cn/news/427610.html

相关文章：

  • 白盒报告-jacoco
  • 【MySQL】SQL语句执行流程
  • Selenium自动化防爬技巧：从入门到精通，保障爬虫稳定运行，通过多种方式和add_argument参数设置来达到破解防爬的目的
  • 从数据类型到变量、作用域、执行上下文
  • 一文读懂：AI时代到底需要什么样的网络？
  • 基于HarmonyOS的宠物收养系统的设计与实现（一）
  • 严格模式报错
  • nginx: [emerg] the “ssl“ parameter requires ngx_http_ssl_module in nginx.conf
  • Docker 部署loki日志 用于微服务
  • [Day 57] 區塊鏈與人工智能的聯動應用：理論、技術與實踐
  • 06结构型设计模式——代理模式
  • 《深入浅出多模态》（九）多模态经典模型：MiniGPT-v2、MiniGPT5
  • 调试和优化大型深度学习模型 - 0 技术介绍
  • 华为S3700交换机配置VLAN的方法​
  • 学懂C++（三十八）：深入详解C++网络编程：套接字（Socket）开发技术
  • SpringBoot-配置加载顺序
  • 第八周：机器学习笔记
  • 音乐怎么剪切掉一部分？5个方法，轻松学会音频分割！（2024全新）
  • 洛谷 CF295D Greg and Caves
  • 【图像处理】在图像处理算法开发中，有哪些常见的主观评价指标和客观评价指标？
  • 从零开始学cv-6：图像的灰度变换
  • 使用Apache POI和POI-OOXML实现word模板文档自动填充功能
  • 【HarmonyOS NEXT星河版开发学习】综合测试案例-各平台评论部分
  • 垂直行业数字化表现抢眼 亚信科技全年利润展望乐观
  • EmguCV学习笔记 VB.Net 4.1 颜色变换
  • 【MySQL进阶之路】表结构的操作
  • 3分钟搞定PDF转PPT！你一定要知道的3款转换神器！
  • 【EasyExcel】导出excel-设置动态表头并导出数据
  • 深入探索 Elasticsearch 8：新特性与核心原理剖析（上）
  • 瑜伽馆预约小程序，在线预约，提高商业价值