【刷题之路Ⅱ】牛客 NC107 寻找峰值
【刷题之路Ⅱ】牛客 NC107 寻找峰值
- 一、题目描述
- 二、解题
- 1、方法1——直接遍历
- 1.1、思路分析
- 1.2、代码实现
- 2、方法2——投机取巧的求最大值
- 2.1、思路分析
- 2.2、代码实现
- 3、方法3——二分法
- 3.1、思路分析
- 3.2、代码实现
一、题目描述
原题连接: NC107 寻找峰值
题目描述:
给定一个长度为n的数组nums,请你找到峰值并返回其索引。数组可能包含多个峰值,在这种情况下,返回任何一个所在位置即可。
1.峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于
2.假设 nums[-1] = nums[n] =−∞
3.对于所有有效的 i 都有 nums[i] != nums[i + 1]
4.你可以使用O(logN)的时间复杂度实现此问题吗?
数据范围:1≤nums.length≤2×10^5
-231<=nums[i]<=231 −1
示例1
输入:[2,4,1,2,7,8,4]
返回值: 1
说明:4和8都是峰值元素,返回4的索引1或者8的索引5都可以
示例2
输入:[1,2,3,1]
返回值: 2
说明:3 是峰值元素,返回其索引 2
二、解题
1、方法1——直接遍历
1.1、思路分析
我们可以直接遍历数组,但有两个情况需要特殊考虑。
当i等于0时,判断nums[i]是否大于nums[i + 1],若大于,则返回i;
当i等于numsLen - 1时,判断nums[i]是否大于nums[i - 1],若大于,则返回i;
其他情况判断是否有nums[i] > nums[i - 1] && nums[i] > nums[i + 1],如果成立,则返回i。
1.2、代码实现
有了以上思路,那我们写起代码来也就水到渠成了:
int findPeakElement1(int* nums, int numsLen) {assert(nums);if (1 == numsLen) {return 0;}int i = 0;for (i = 0; i < numsLen; i++) {if (0 == i) {if (nums[i] > nums[i + 1]) {return i;}}else if (numsLen - 1 == i) {if (nums[i] > nums[i - 1]) {return i;}}else if (nums[i] > nums[i - 1] && nums[i] > nums[i + 1]) {return i;}}return -1;
}
时间复杂度:O(n),n为数组元素个数。
空间复杂度:O(1),我们只需要用到常数级的额外空间
2、方法2——投机取巧的求最大值
2.1、思路分析
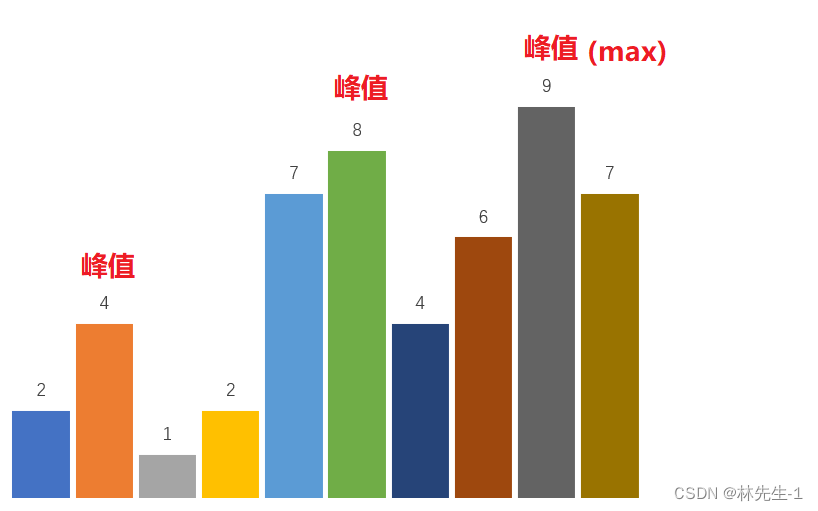
根据题目的描述:“对于所有有效的 i 都有 nums[i] != nums[i + 1]”,且返回任意一个就行。
就有一个非常投机取巧的方法就是直接找到数组中的最大值,返回其下标就行了。
这个方法之所有有效是因为峰值不一定是最大值,但最大值一定是峰值。😏
2.2、代码实现
有了以上思路,那我们写起代码来也就水到渠成了:
int findPeakElement2(int* nums, int numsLen) {assert(nums);if (1 == numsLen) {return 0;}int max = nums[0];int index = 0;int i = 0;for (i = 1; i < numsLen; i++) {if (nums[i] > max) {max = nums[i];index = i;}}return index;
}
时间复杂度:O(n),n为数组元素个数,我们只需要遍历一遍数组即可。
空间复杂度:O(1),我们只需要用到常数级的额外空间。
3、方法3——二分法
3.1、思路分析
我们其实可以使用二分法来是我们的left和right每一次都向"峰值"靠近。
当left和right重合时即找到了峰值。
具体做法如下:
1、当nums[mid] < nums[mid + 1]时,说明从下标mid到下标mid + 1是在走上坡路:
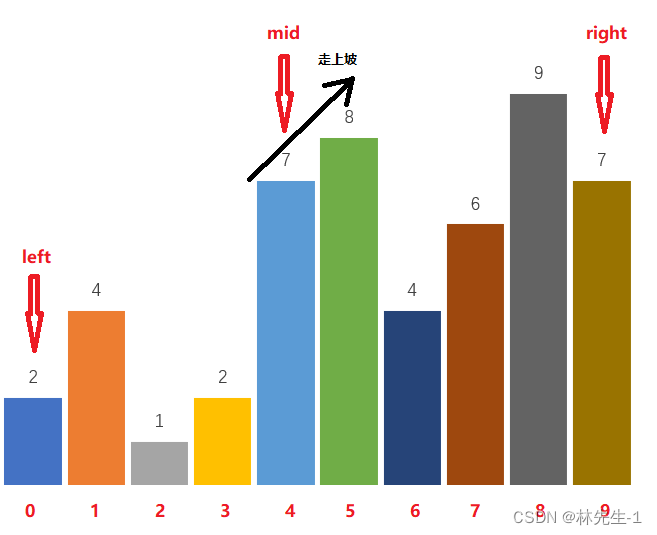
则可以肯定此时的mid一定不是峰值,所以执行left = mid + 1,使区间向峰值靠近。
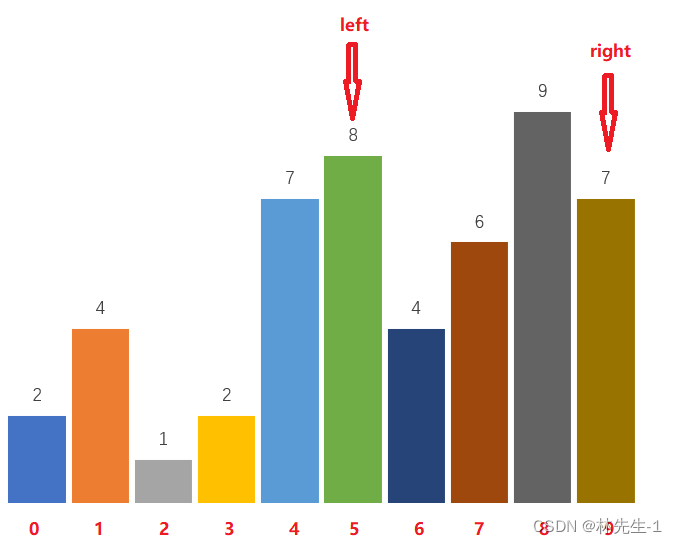
2、当nums[mid] > nums[mid + 1]时,说明从下标mid到下标mid + 1是在走下坡路:
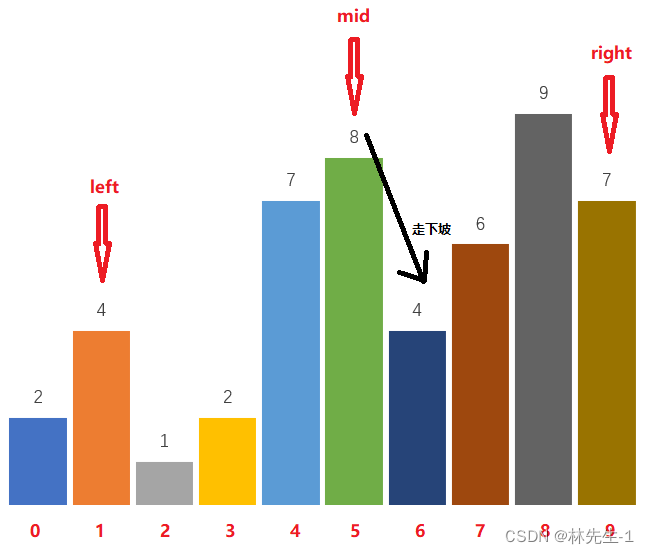
则mid可能是峰值,此时应该执行right = mid(不能跳过mid,因为mid可能是峰值),使区间向峰值靠近。
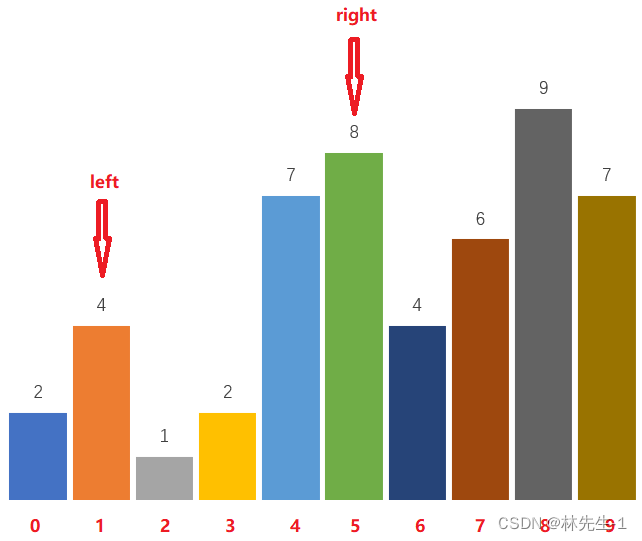
最后当left和right重合时,说明我们已经找到了峰值。
3.2、代码实现
有了以上思路,那我们写起代码来也就水到渠成了:
int findPeakElement3(int* nums, int numsLen) {assert(nums);int left = 0;int right = numsLen - 1;int mid = 0;while (left < right) {mid = left + (right - left) / 2;if (nums[mid] < nums[mid + 1]) {left = mid + 1;}else {right = mid;}}return left;
}
时间复杂度:O(log2N),其中N为数组元素个数,最坏情况下,我们要对整个数组进行二分,所以时间复杂度为O(log2N)。
空间复杂度:O(1),我们只需要用到常数级的额外空间。
