当前位置：首页 > news >正文

使用太极taichi写一个只有一个三角形的有限元

news 2025/7/14 15:19:07

公式来源

https://blog.csdn.net/weixin_43940314/article/details/128935230

GAME103
https://games-cn.org/games103-slides/

初始化我们的三角形

全局的坐标范围为0-1

我们的三角形如图所示

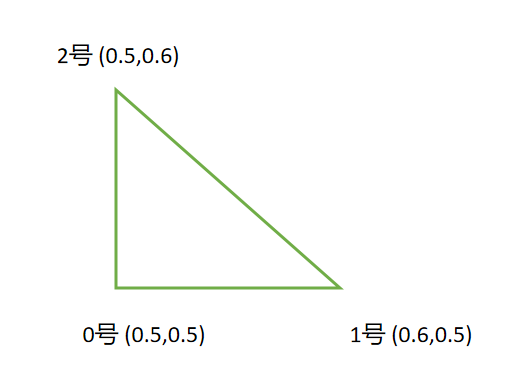
在这里插入图片描述

@ti.kernel
def init():X[0] = [0.5, 0.5]X[1] = [0.5, 0.6]X[2] = [0.6, 0.5]x[0] = X[0] + [0, 0.01]x[1] = X[1]x[2] = X[2]

X是rest pos
x是current pos

这里给一个小的增量是为了看出来被拉了，否则产生不了弹性力

公式抄录

$[f1f2]=−ArefFS[X10X20]−T\begin{bmatrix} \mathbf{f_1} & \mathbf{f_2} \end{bmatrix}= -A^{ref} \mathbf{F} \mathbf{S } \begin{bmatrix} \mathbf{X_{10}} & \mathbf{X_{20}} \end{bmatrix}^{-T}$

$F=[x10x20][X10X20]−1F=\begin{bmatrix} x_{10} & x_{20} \end{bmatrix}\begin{bmatrix} X_{10} & X_{20} \end{bmatrix}^{-1}$

$\mu G + \lambda trace(C) I$

$\frac{1}{2} (F^T F -I)$

0. 设定一下材料参数

dim=2
n_particles = 3
n_elements = 1
area = 0.1*0.1*0.5
dt = 1e-4
E, nu = 1e3, 0.33  # Young's modulus and Poisson's ratio
mu, lam = E / 2 / (1 + nu), E * nu / (1 + nu) / (1 - 2 * nu)  # Lame parameters

1 计算F

根据上面的公式，我们要先算F

@ti.kernel
def substep():#compute deformation gradientfor i in range(n_elements):Dm =ti.Matrix([[x[1][0]-x[0][0], x[2][0]-x[0][0]], [x[1][1]-x[0][1], x[2][1]-x[0][1]]])Dm_inv[i] = Dm.inverse()Ds = ti.Matrix([[X[1][0]-X[0][0], X[2][0]-X[0][0]], [X[1][1]-X[0][1], X[2][1]-X[0][1]]])F[i] = Ds @ Dm_inv[i]

2 计算格林应变

#compute green strain
for i in range(n_elements):G[i] = 0.5 * (F[i].transpose() @ F[i] - ti.Matrix([[1, 0], [0, 1]]))

3 计算PK1

#compute second Piola Kirchhoff stress
for i in range(n_elements):S[i] = 2 * mu *G[i] + lam * (G[i][0,0]+G[i][1,1]) * ti.Matrix([[1, 0], [0, 1]])

4 计算粒子上的力

#compute force(先暂且就计算一个三角形的力，后面再考虑多个三角形的情况)
force_matrix =  F[0] @ S[0] @ Dm_inv[0].transpose() * area
force[1] = ti.Vector([force_matrix[0, 0], force_matrix[1, 0]])
force[2] = ti.Vector([force_matrix[0, 1], force_matrix[1, 1]])
force[0] = -force[1] - force[2]

5 加个重力

    #gravityfor i in range(n_particles):force[i][1] -= 0.1

6 时间积分同时处理边界条件

    #time integration(with boundary condition)eps = 0.01for i in range(n_particles):vel[i] += dt * force[i]#boundary conditioncond = (x[i] < eps) & (vel[i] < 0) | (x[i] > 1) & (vel[i] > eps)for j in ti.static(range(dim)):if cond[j]:vel[i][j] = 0  x[i] += dt * vel[i]

完整的程序

# ref: https://blog.csdn.net/weixin_43940314/article/details/128935230import taichi as ti
import numpy as npti.init(arch=ti.cpu, debug=True)dim=2
n_particles = 3
n_elements = 1
area = 0.1*0.1*0.5
# lam = 1
# mu = 1
dt = 1e-4
E, nu = 1e3, 0.33  # Young's modulus and Poisson's ratio
mu, lam = E / 2 / (1 + nu), E * nu / (1 + nu) / (1 - 2 * nu)  # Lame parametersx = ti.Vector.field(dim, dtype=float, shape=n_particles) #deformed position
force = ti.Vector.field(dim, dtype=float, shape=n_particles)
vel = ti.Vector.field(dim, dtype=float, shape=n_particles)
X = ti.Vector.field(dim, dtype=float, shape=n_particles) #undeformed position
S = ti.Matrix.field(n=dim, m=dim, dtype=float, shape=n_elements) #Second Piola Kirchhoff stress
F = ti.Matrix.field(n=dim, m=dim, dtype=float, shape=n_elements) #deformation gradient
G = ti.Matrix.field(n=dim, m=dim, dtype=float, shape=n_elements) #green strain@ti.kernel
def init():X[0] = [0.5, 0.5]X[1] = [0.5, 0.6]X[2] = [0.6, 0.5]x[0] = X[0] + [0, 0.01]x[1] = X[1]x[2] = X[2]Dm_inv = ti.Matrix.field(n=dim, m=dim, dtype=float, shape=n_elements) 
@ti.kernel
def substep():#compute deformation gradientfor i in range(n_elements):Dm =ti.Matrix([[x[1][0]-x[0][0], x[2][0]-x[0][0]], [x[1][1]-x[0][1], x[2][1]-x[0][1]]])Dm_inv[i] = Dm.inverse()Ds = ti.Matrix([[X[1][0]-X[0][0], X[2][0]-X[0][0]], [X[1][1]-X[0][1], X[2][1]-X[0][1]]])F[i] = Ds @ Dm_inv[i]# print(F[0])#compute green strainfor i in range(n_elements):G[i] = 0.5 * (F[i].transpose() @ F[i] - ti.Matrix([[1, 0], [0, 1]]))#compute second Piola Kirchhoff stressfor i in range(n_elements):S[i] = 2 * mu *G[i] + lam * (G[i][0,0]+G[i][1,1]) * ti.Matrix([[1, 0], [0, 1]])#compute force(先暂且就计算一个三角形的力，后面再考虑多个三角形的情况)force_matrix =  F[0] @ S[0] @ Dm_inv[0].transpose() * areaforce[1] = ti.Vector([force_matrix[0, 0], force_matrix[1, 0]])force[2] = ti.Vector([force_matrix[0, 1], force_matrix[1, 1]])force[0] = -force[1] - force[2]# print(force[0])#gravityfor i in range(n_particles):force[i][1] -= 0.1#time integration(with boundary condition)eps = 0.01for i in range(n_particles):vel[i] += dt * force[i]#boundary conditioncond = (x[i] < eps) & (vel[i] < 0) | (x[i] > 1) & (vel[i] > eps)for j in ti.static(range(dim)):if cond[j]:vel[i][j] = 0  x[i] += dt * vel[i]def main():init()gui = ti.GUI('my', (1024, 1024))while gui.running:for e in gui.get_events():if e.key == gui.ESCAPE:gui.running = Falseelif e.key == 'r':init()for i in range(30):substep()vertices_ = np.array([[0, 1, 2]], dtype=np.int32)particle_pos = x.to_numpy()a = vertices_.reshape(n_elements * 3)b = np.roll(vertices_, shift=1, axis=1).reshape(n_elements * 3)gui.lines(particle_pos[a], particle_pos[b], radius=1, color=0x4FB99F)gui.circles(particle_pos, radius=5, color=0xF2B134)gui.show()if __name__ == '__main__':main()