线性代数之矩阵
一、思维导图
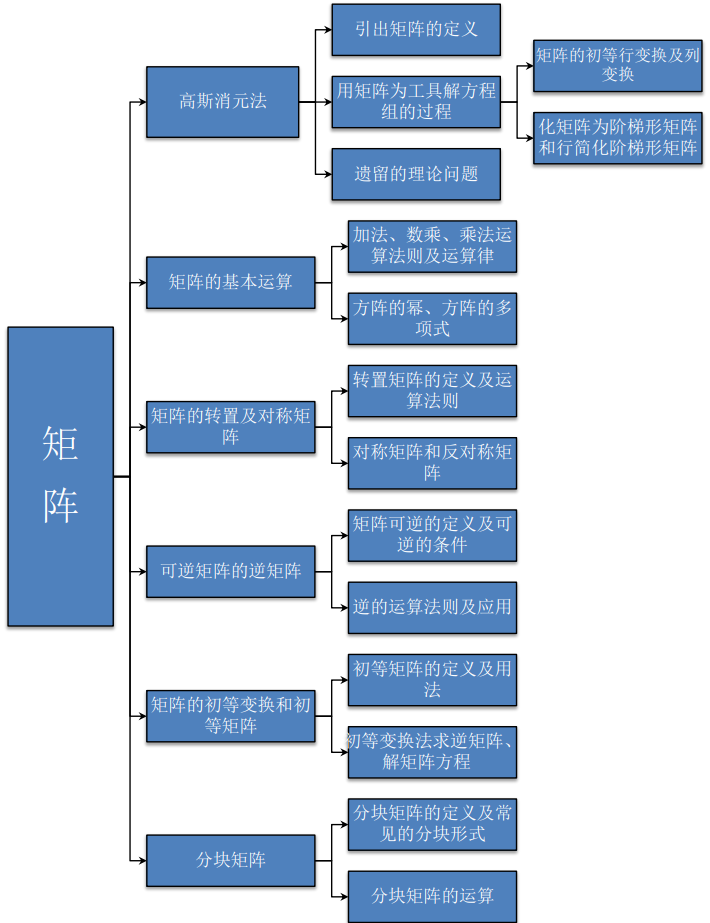
二、矩阵及其运算
1、矩阵的定义

注:

零矩阵:元素均为0 的矩阵,通常记作0
m*n称为矩阵的类型。
满足阶梯形矩阵
行简化的阶梯形矩阵即满足如下条件的矩阵: (1)阶梯形; (2)非零首元所在列其余元素均为0 ; (3) 非零首元均是1.

2、运算法则
2.1 矩阵加法

2.2 矩阵的数量乘法

2.3 矩阵的乘积
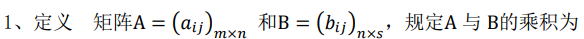

3、几个特别的矩阵
3.1 𝑛阶单位矩阵
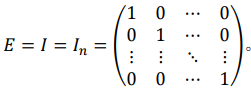
3.2 𝑛阶数量矩阵
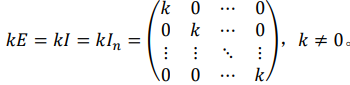
3.3 对角矩阵

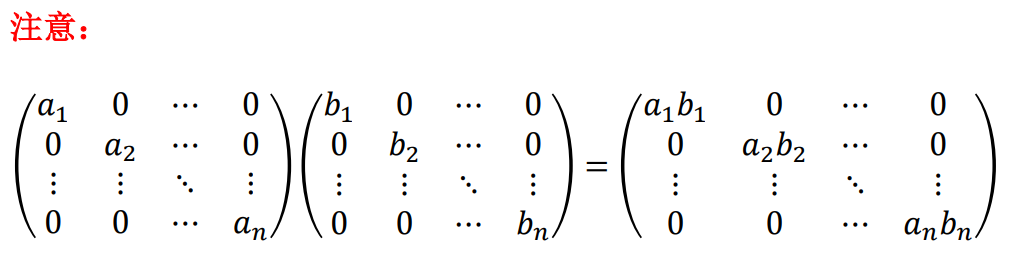
3.4 上(下)三角矩阵


3.5 结论

4、定理 若矩阵𝑨,𝑩为同阶方阵,则 𝑨𝑩 = |𝑨 | | �� |。
5、方阵的幂和方阵的多项式

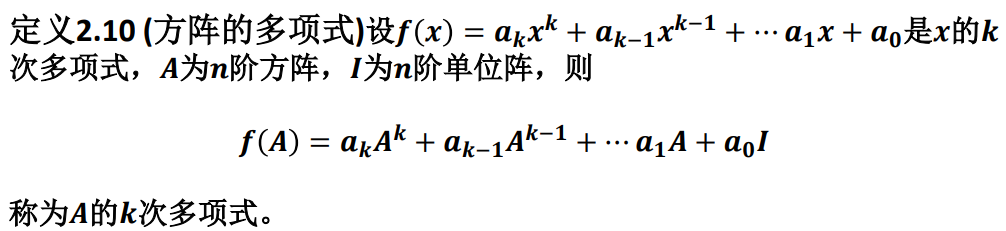

6、转置与对称




7、可逆矩阵
7.1 逆矩阵

定理 若𝑨是可逆矩阵,则𝑨的逆矩阵是唯一的
7.2 伴随矩阵


7.3 运算律

三、矩阵的初等变换和初等矩阵
1、初等变换

2、初等矩阵
初等矩阵:单位矩阵经过一次初等变换所得到的矩阵



作用
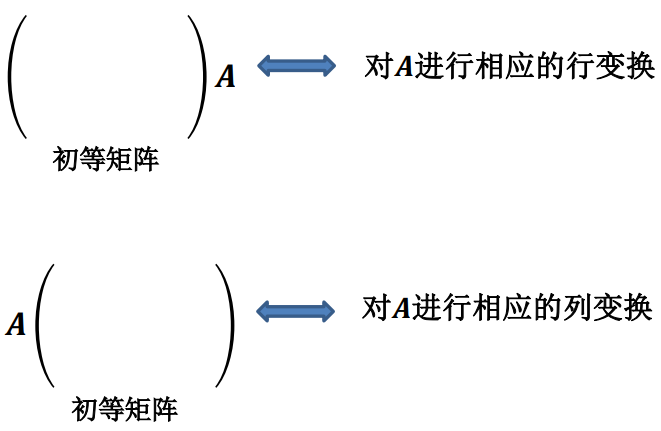
3、初等变换法求逆矩阵

4、初等变换法解矩阵方程


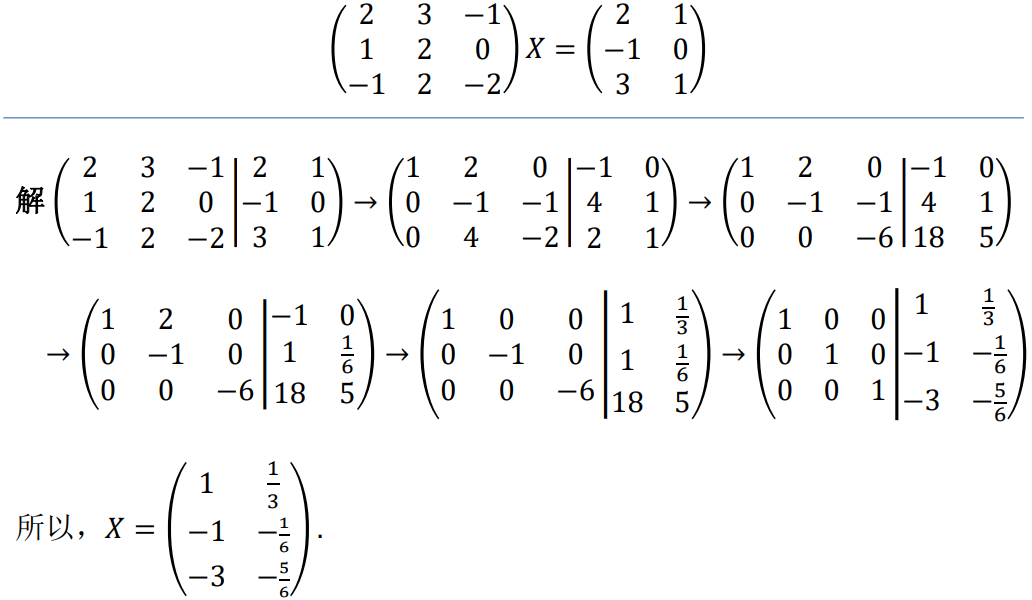

四、复习题

