当前位置：首页 > news >正文

【Python实战因果推断】31_双重差分2

news 2025/7/13 17:00:32

Canonical Difference-in-Differences

Diff-in-Diff with Outcome Growth

Canonical Difference-in-Differences

差分法的基本思想是，通过使用受治疗单位的基线，但应用对照单位的结果（增长）演变，来估算缺失的潜在结果 $E[Y(0)|D=1,Post=1]$ ：

$\begin{aligned}E[Y(0)|D=1,Post=1]&=E[Y|D=1,Post=0]\\&+(E[Y|D=0,Post=1]-E[Y|D=0,Post=0])\end{aligned}$

其中，用样本平均数代替右侧期望值，就可以估计出 $E[Y(0)|D=1,Post=1]$ 。之所以称其为 "差异-差分（DID）估计法"，是因为如果将前述表达式替换为 ATT 中的 $E[Y(0)|D=1,Post=1]$ ，就会得到 "差异中的差异"：

$\begin{aligned}ATT&=(E[Y|D=1,Post=1]-E[Y|D=1,Post=0])\\&-(E[Y|D=0,Post=1]-E[Y|D=0,Post=0])\end{aligned}$

不要被这些期望吓倒。以其典型形式，您可以很容易地得到 DID 估计值。首先，将数据的时间段分为干预前和干预后。然后，将单位分为治疗组和对照组。最后，您可以简单地计算所有四个单元的平均值：干预前与对照组、干预前与干预组、干预后与对照组、干预后与干预组：

 did_data = (mkt_data.groupby(["treated", "post"]).agg({"downloads":"mean", "date": "min"}))did_data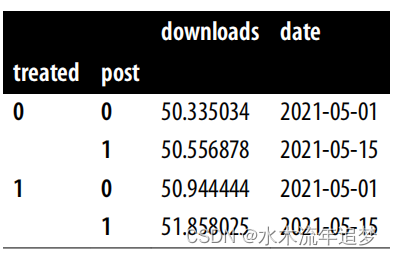

这些就是获得 DID 估计值所需的全部数据。对于干预基线 $E[Y|D=1,Post=0]$ ，您可以使用 did_data.loc[1] 将其索引到干预中，然后使用 follow up .loc[0] 将其索引到干预前。要得到对照组结果的变化，即 $E[Y|D=0,Post=1]-E[Y|D=0,Post=0]$ ，可以用 did_data.loc[0] 索引到对照组，用 .diff() 计算差值，然后用后续 .loc[1] 索引到最后一行。将对照组趋势与治疗基线相加，就得到了反事实 $E[ Y(0) |D=1,Post=1 ]$ 的估计值。要得到 ATT，可以用干预后期间受治疗者的平均结果减去 ATT：

 y0_est = (did_data.loc[1].loc[0, "downloads"] # treated baseline# control evolution+ did_data.loc[0].diff().loc[1, "downloads"])att = did_data.loc[1].loc[1, "downloads"] - y0_estatt0.6917359536407233

如果将这个数字与真实 ATT（过滤干预单位和干预后时期）进行比较，可以发现 DID 估计值与其试图估计的结果相当接近：

 mkt_data.query("post==1").query("treated==1")["tau"].mean()0.7660316402518457

Diff-in-Diff with Outcome Growth

对 DID 的另一个非常有趣的理解是，它是在时间维度上对数据进行区分。让我们把单位 i 在不同时间的结果差异定义为 $\Delta y_{i}=E\Big[y_{i}\Big|t>T_{pre}\Big]-E\Big[y_{i}\Big|t\leq T_{pre}\Big]$ 。现在，让我们把按时间和单位划分的原始数据转换成一个带有 Δyi 的数据框架，其中时间维度已被区分出来：

 pre = mkt_data.query("post==0").groupby("city")["downloads"].mean()post = mkt_data.query("post==1").groupby("city")["downloads"].mean()delta_y = ((post - pre).rename("delta_y").to_frame()# add the treatment dummy.join(mkt_data.groupby("city")["treated"].max()))delta_y.tail()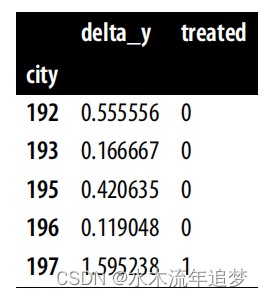

接下来，您可以使用潜在的结果符号来根据Δy来定义ATT $ATT=E[\Delta y_1-\Delta y_0],$

DID试图通过用控制单元的平均值替换Δy0来识别哪个控制单元： $ATT=E[\Delta y|D=1]-E[\Delta y|D=0]$

如果你用样本平均值来代替这些期望，你会看到你得到了和之前相同的估计：

 (delta_y.query("treated==1")["delta_y"].mean()- delta_y.query("treated==0")["delta_y"].mean())0.6917359536407155

这是对 DID 的一个有趣的解释，因为它非常清楚地说明了它的假设，即 $E[\Delta y_{0}]=E[\Delta y|D=0]$ ，但我们稍后会进一步讨论这个问题。

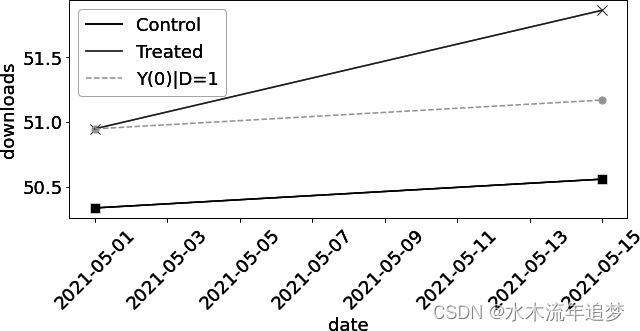
由于这些都是非常专业的数学知识，我想通过绘制治疗组和对照组随时间变化的观察结果，以及治疗组的估计反事实结果，让大家对 DID 有更直观的理解。在下图中， $E[Y(0)|D=1]$ 的 DID 估计结果以虚线表示。它是通过将对照组的轨迹应用到干预基线中得到的。因此，估计的 ATT 将是估计的反事实结果 $Y(0)$ 与观察到的结果 $Y(1)$ 之间的差值，两者均处于干预后时期（圆点与十字之间的差值）：