当前位置：首页 > news >正文

【深度学习】第3章——回归模型与求解分析

news 2025/8/3 22:51:37

一、回归分析

1.定义

分析自变量与因变量之间定量的因果关系，根据已有的数据拟合出变量之间的关系。

2.回归和分类的区别和联系

3.线性模型

4.非线性模型

5.线性回归※

面对回归问题，通常分三步解决

第一步：选定使用的model，即确定函数模型是一次函数还是二次函数，甚至是更高的三次四次或者五次函数。

第二步：确定模型的损失函数loss function。

均方误差损失函数（MSE）的公式如下：

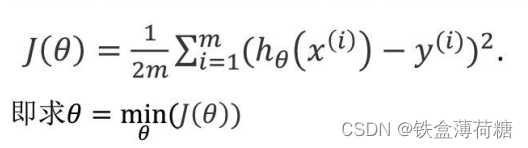
第三步：采用梯度下降，优化损失函数 (可以使用梯度下降的前提是损失函数可微分)。

二、多元回归与多项式回归

1.Sklearn的一元线性回归

在scikit-learn中，所有的估计器都带有fit( )方法和predict( )方法

fit()用来拟合模型，predict()利用拟合出来的模型对样本进行预测。

例如：

from sklearn.linear_model import LinearRegression# 创建并拟合模型
model = LinearRegression()
X = [[6], [8], [10], [14], [18]]
y = [[7], [9], [13], [17.5], [18]]
model.fit(X, y)# 预测12英寸披萨的价格
predict方法的输入应当是一个2D数组，而不是一个单独的整数。
#例如：predicted = model.predict([[12], [16]])
#predicted_price_12 = predicted[0][0]  # 15.0
#predicted_price_16 = predicted[1][0]  # 20.0predicted_price = model.predict([[12]])[0][0]
print('预测12英寸披萨价格: $%.2f' % predicted_price)

2.多元线性回归

from sklearn.linear_model import LinearRegressionX = [[6, 2], [8, 1], [10, 0], [14, 2], [18, 0]]
# 特征数据集，包含两个特征：披萨尺寸和其他因素（例如配料数量）
y = [[7], [9], [13], [17.5], [18]]
# 目标数据集，披萨价格model = LinearRegression()
# 创建线性回归模型实例
model.fit(X, y)
# 使用特征数据X和目标数据y训练模型X_test = [[8, 2], [9, 0], [11, 2], [16, 2], [12, 0]]
# 测试数据集，包含待预测的披萨尺寸和其他因素
y_test = [[11], [8.5], [15], [18], [11]]
# 测试目标数据集，对应测试数据集的实际披萨价格predictions = model.predict(X_test)
# 使用训练好的模型预测测试数据集的披萨价格for i, prediction in enumerate(predictions):# 遍历预测结果print('Predicted: %s, Target: %s' % (prediction, y_test[i]))# 输出预测价格和实际目标价格print('R-squared: %.2f' % model.score(X_test, y_test))
# 计算并输出模型在测试数据集上的R-squared值，表示模型的拟合优度

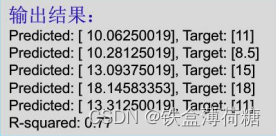
其中，model.score(X_test, y_test)是在计算模型在 X_test 数据集上预测的 y_test 值与实际 y_test 值之间的拟合优度，即R-squared 值（决定系数），它表示目标变量的方差有多少可以通过特征变量来解释。

3.多项式回归

三、损失函数的正则化

from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score# 加载数据集
data = load_iris()
X, y = data.data, data.target# 定义模型
model = LogisticRegression(max_iter=200)# 定义正则化参数的网格
param_grid = {'C': [0.01, 0.1, 1, 10, 100]
}# 使用 GridSearchCV 进行超参数搜索
grid_search = GridSearchCV(model, param_grid, cv=5, scoring='accuracy')
grid_search.fit(X, y)# 输出最佳参数和最佳分数
print("Best parameters found: ", grid_search.best_params_)
print("Best cross-validation score: ", grid_search.best_score_)# 使用最佳参数训练模型
best_model = grid_search.best_estimator_
best_model.fit(X, y)# 预测并计算准确率
y_pred = best_model.predict(X)
print("Training accuracy: ", accuracy_score(y, y_pred))