Python28-7.5 降维算法之t-分布邻域嵌入t-SNE
t-分布邻域嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)是一种用于数据降维和可视化的机器学习算法,尤其适用于高维数据的降维。t-SNE通过将高维数据嵌入到低维空间(通常是二维或三维)中,使得在高维空间中相似的点在低维空间中仍然保持相似,而不相似的点被分离开来。
t-SNE的基本原理
t-SNE通过两步将高维数据降维:
-
计算高维空间中的相似性:在高维空间中,t-SNE使用高斯分布来计算数据点之间的相似性。给定数据点x_i和 x_j,其相似性 p_ij定义为:
这里,sigma_i 是根据Perplexity参数自动确定的。
-
计算低维空间中的相似性:在低维空间中,t-SNE使用t分布来计算数据点之间的相似性。给定低维数据点 y_i和 y_j,其相似性 q_ij定义为:
-
最小化KL散度:t-SNE通过最小化高维相似性分布 (P) 和低维相似性分布 (Q) 之间的Kullback-Leibler (KL) 散度来优化低维嵌入:
t-SNE的特点
-
保持局部结构:t-SNE在保持数据局部结构(局部相似性)方面表现非常好,能够揭示数据中的细节模式。
-
非线性降维:t-SNE是非线性降维方法,适合处理具有复杂非线性结构的数据。
-
高计算量:t-SNE计算量较大,尤其是在处理大规模数据集时。
t-SNE的应用
t-SNE广泛应用于数据可视化,特别是以下领域:
-
图像处理:用于高维图像特征的可视化。
-
自然语言处理:用于文本和词嵌入的可视化。
-
生物信息学:用于基因表达数据的可视化。
-
聚类分析:用于聚类结果的可视化。
示例代码
以下是使用Python库scikit-learn实现t-SNE的示例代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from sklearn.datasets import load_digits# 加载数据
digits = load_digits()
X = digits.data
y = digits.target# 使用t-SNE降维
tsne = TSNE(n_components=2, perplexity=30, n_iter=300)
X_embedded = tsne.fit_transform(X)# 可视化结果
plt.figure(figsize=(10, 8))
scatter = plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c=y, cmap='viridis')
plt.colorbar(scatter)
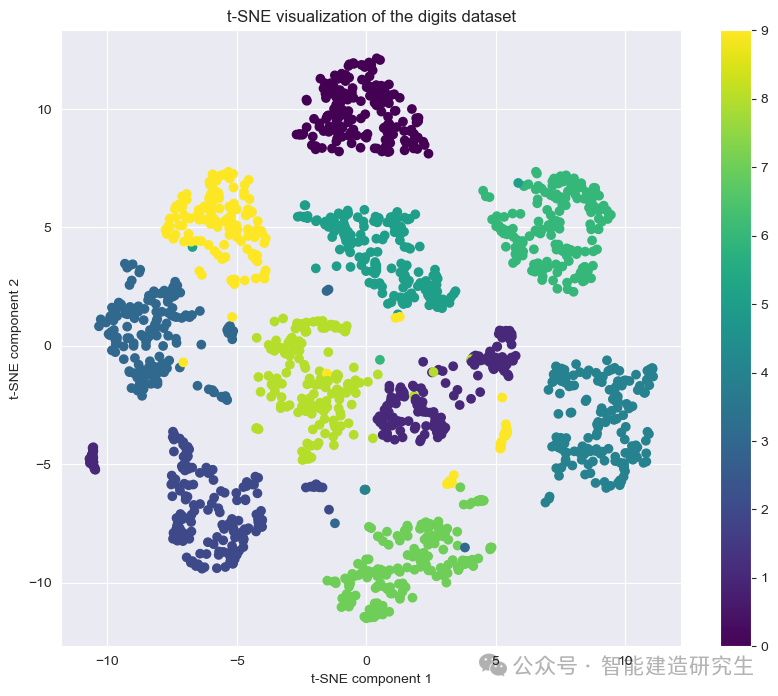
plt.title("t-SNE visualization of the digits dataset")
plt.xlabel("t-SNE component 1")
plt.ylabel("t-SNE component 2")
plt.show()
t-SNE的参数调整
-
Perplexity:影响高斯分布的方差,通常介于5到50之间,反映了考虑邻居数量的平衡。
-
学习率(learning_rate):影响梯度下降的步长,通常设置在10到1000之间。
-
迭代次数(n_iter):t-SNE优化过程的迭代次数,通常需要至少250次迭代,建议300次以上。
t-SNE是一种强大的非线性降维方法,特别适用于高维数据的可视化。通过保持高维数据的局部结构,它能够揭示数据中的复杂模式。然而,t-SNE的计算复杂度较高,需要合理选择参数来平衡性能和效果。
以上内容总结自网络,如有帮助欢迎转发,我们下次再见!
