Python28-7.4 独立成分分析ICA分离混合音频
独立成分分析(Independent Component Analysis,ICA)是一种统计与计算技术,主要用于信号分离,即从多种混合信号中提取出独立的信号源。ICA在处理盲源分离(Blind Source Separation,BSS)问题时尤为有效,如从录音中分离出不同的声音源、从脑电图(EEG)中提取出独立的神经活动信号等。
ICA的基本原理
ICA假设观察到的信号是若干独立信号源线性混合的结果。目标是从这些观察到的信号中恢复出原始的独立信号源。
假设有
个观测信号,这些信号是由 个独立信号源通过一个未知的线性混合矩阵线性组合得到的,即:
ICA的目标是找到一个解混合矩阵
,使得:
其中
是估计的独立成分向量,尽可能接近原始的独立信号源。
ICA的假设条件
-
独立性假设:信号源彼此之间相互独立。
-
非高斯性假设:独立成分(信号源)遵循非高斯分布。这一假设是ICA区分独立成分的关键。
主要算法
ICA有多种实现算法,其中比较常用的包括:
-
FastICA:一种迭代算法,通过最大化非高斯性(如负熵)来估计独立成分。
-
Infomax ICA:基于最大化信息传输的算法,通过最大化信号的熵来实现信号分离。
-
**JADE (Joint Approximate Diagonalization of Eigen-matrices)**:基于四阶累积量矩阵的联合近似对角化来分离独立成分。
应用领域
-
生物医学信号处理:如脑电图(EEG)、心电图(ECG)信号的分离和分析。
-
语音信号处理:从混合录音中分离出不同的语音源。
-
图像处理:在图像去噪、特征提取等方面应用广泛。
-
金融数据分析:用于分离和识别金融时间序列中的独立成分。
优点与局限性
优点:
-
能够有效地分离出相互独立的信号源。
-
适用于各种信号处理领域,应用广泛。
局限性:
-
对混合矩阵的精确估计要求较高。
-
对信号源的独立性和非高斯性有较强的假设,实际应用中可能不完全满足。
-
算法复杂度较高,计算量大。
实例
以下是使用Python库Scikit-learn进行ICA分析的一个简单示例:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import FastICA# 生成混合信号
np.random.seed(0)
time = np.linspace(0, 1, 200)
S1 = np.sin(2 * np.pi * 1 * time) # 正弦波
S2 = np.sign(np.sin(3 * np.pi * 2 * time)) # 方波
S = np.c_[S1, S2]
S += 0.1 * np.random.normal(size=S.shape) # 添加噪声# 混合信号
A = np.array([[1, 1], [0.5, 2]]) # 混合矩阵
X = np.dot(S, A.T) # 观测信号# 使用FastICA进行独立成分分析
ica = FastICA(n_components=2)
S_ = ica.fit_transform(X) # 估计的信号源
A_ = ica.mixing_ # 估计的混合矩阵# 绘制信号
plt.figure(figsize=(10, 8))plt.subplot(3, 1, 1)
plt.title("Original Signals")
plt.plot(time, S[:, 0], label='Signal 1')
plt.plot(time, S[:, 1], label='Signal 2')
plt.legend()plt.subplot(3, 1, 2)
plt.title("Mixed Signals")
plt.plot(time, X[:, 0], label='Mixed Signal 1')
plt.plot(time, X[:, 1], label='Mixed Signal 2')
plt.legend()plt.subplot(3, 1, 3)
plt.title("ICA Recovered Signals")
plt.plot(time, S_[:, 0], label='Recovered Signal 1')
plt.plot(time, S_[:, 1], label='Recovered Signal 2')
plt.legend()plt.tight_layout()
plt.show()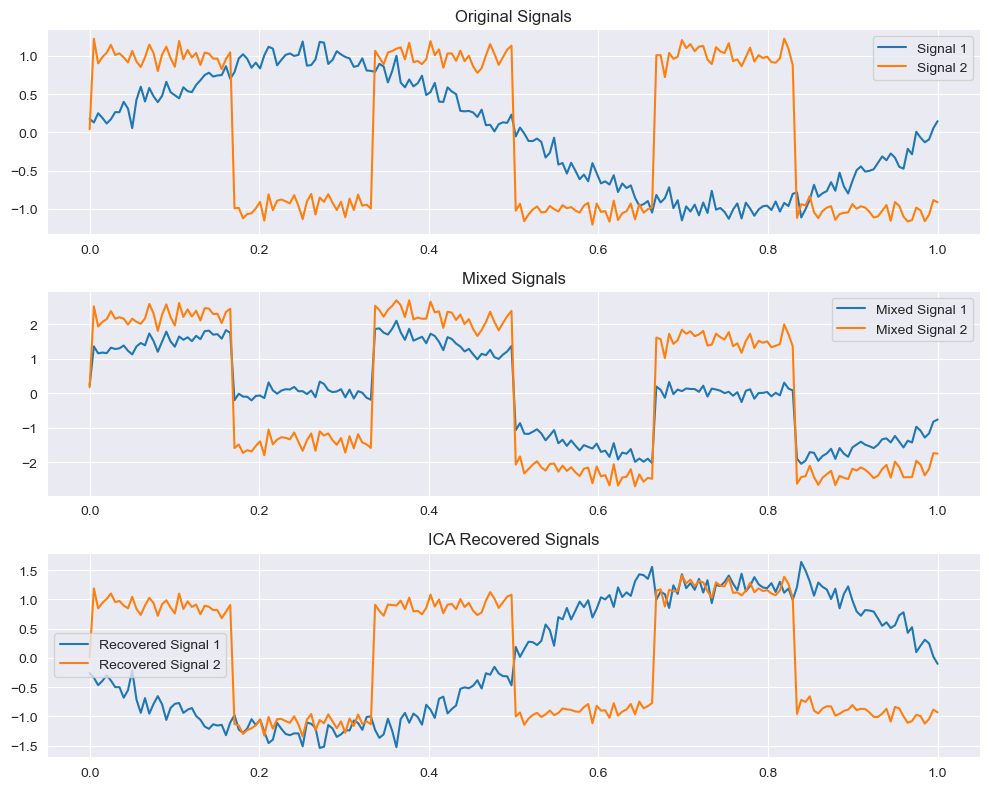
这段代码将生成三个子图:
-
原始信号:显示最初生成的两个独立信号(一个正弦波和一个方波)。
-
混合信号:显示通过混合矩阵生成的两个观测信号。
-
分离出的信号:显示通过ICA分离出的信号,它们应该与原始信号非常相似。
其中:
-
原始信号显示了生成的两个独立信号。
-
混合信号展示了线性组合后的混合信号。
-
分离出的信号是通过ICA算法分离出的两个独立信号,它们应尽可能接近原始信号。
通过上述代码,可以将混合信号分离成独立的信号源,从而实现信号分离的目的。
我们继续使用网上公开的音乐文件对其进行混合处理后,再使用FastICA进行独立成分分析。
原始音频:
music1(SalmonLikeTheFish - Glacier):
music2(Aitua - Johann Pachelbel - Kanon in D Dur):
由于设置采样按照最短的音频文件进行采样,因此混合后的音频和最终独立成分分析之后的音频都只是3:21的长度。
ICA独立成分分析处理:
import os
import numpy as np
import matplotlib.pyplot as plt
import librosa
import soundfile as sf
from sklearn.decomposition import FastICA# 设置音频文件目录
audio_dir = 'MusicMix'
music1_path = os.path.join(audio_dir, 'music1.wav')
music2_path = os.path.join(audio_dir, 'music2.wav')# 检查音频文件是否存在
if not os.path.exists(music1_path) or not os.path.exists(music2_path):raise FileNotFoundError("请确保所有音频文件已下载并放置在正确的目录中。")# 加载音频文件
music1, sr1 = librosa.load(music1_path, sr=None)
music2, sr2 = librosa.load(music2_path, sr=None)# 确保采样率相同
if sr1 != sr2:raise ValueError("两个音频文件的采样率不同。")# 使两个音频文件具有相同的长度
min_len = min(len(music1), len(music2))
music1 = music1[:min_len]
music2 = music2[:min_len]# 创建混合信号
mix1 = music1 + music2
mix2 = 0.5 * music1 + music2# 创建混合信号矩阵
X = np.c_[mix1, mix2]# 使用FastICA进行独立成分分析
ica = FastICA(n_components=2, max_iter=1000, tol=0.001)
S_ = ica.fit_transform(X) # 估计的信号源
A_ = ica.mixing_ # 估计的混合矩阵# 绘制信号
time = np.arange(len(mix1)) / sr1plt.figure(figsize=(10, 8))plt.subplot(3, 1, 1)
plt.title("Original Music Signals")
plt.plot(time, music1, label='Music 1')
plt.plot(time, music2, label='Music 2')
plt.legend()plt.subplot(3, 1, 2)
plt.title("Mixed Music Signals")
plt.plot(time, mix1, label='Mixed Signal 1')
plt.plot(time, mix2, label='Mixed Signal 2')
plt.legend()plt.subplot(3, 1, 3)
plt.title("ICA Recovered Music Signals")
plt.plot(time, S_[:, 0], label='Recovered Signal 1')
plt.plot(time, S_[:, 1], label='Recovered Signal 2')
plt.legend()plt.tight_layout()
plt.show()# 保存混合后的音频信号
sf.write(os.path.join(audio_dir, 'mixed1.wav'), mix1, sr1)
sf.write(os.path.join(audio_dir, 'mixed2.wav'), mix2, sr1)# 保存分离后的音频信号
sf.write(os.path.join(audio_dir, 'recovered1.wav'), S_[:, 0], sr1)
sf.write(os.path.join(audio_dir, 'recovered2.wav'), S_[:, 1], sr1)波形图输出:
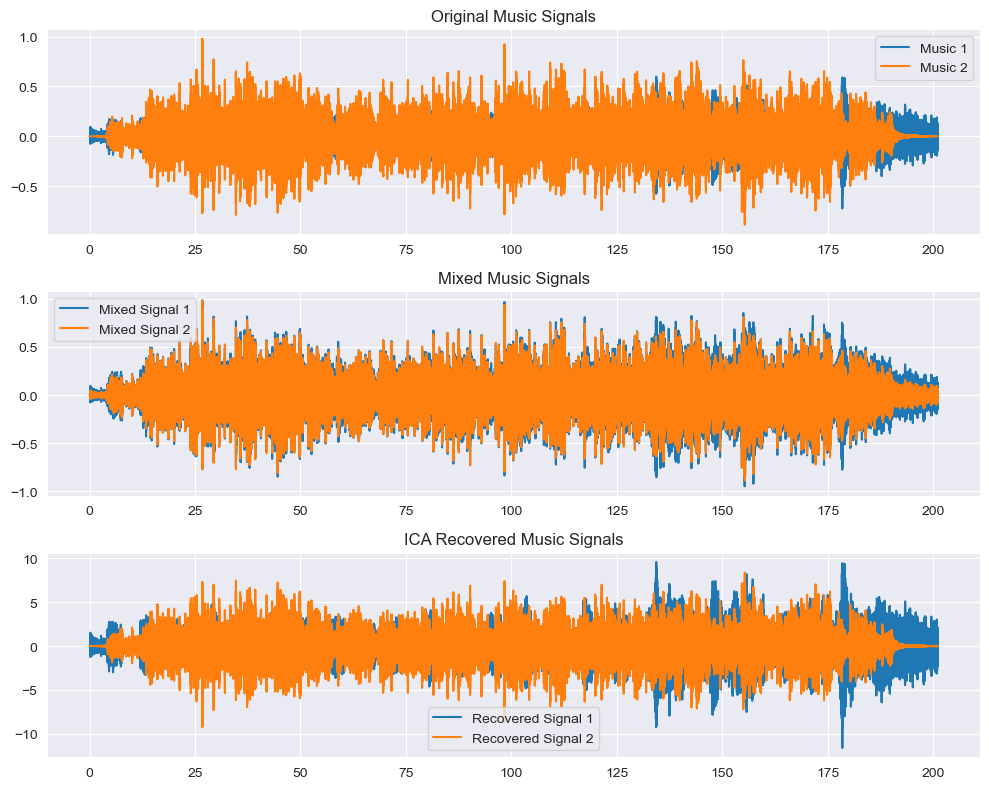
重新分离出的两段音乐:
从以上两个音频的输出可知,ICA成功分离出了两手不同的歌曲,虽然音质回有部分损失。我们实现了将两个音乐信号混合,并使用ICA技术将它们分离回原始的独立信号。关键步骤包括确保采样率一致、对齐音频长度、创建混合信号以及应用ICA算法。结果显示在图表中,并保存为音频文件供进一步分析和使用。这一过程展示了ICA在信号处理中的强大应用,特别是对于混合音频信号的分离。
以上内容总结自网络,如有帮助欢迎转发,我们下次再见!
