密码学复习
目录
基础
欧拉函数
欧拉函数φ(n)定义
计算方法的技巧
当a=a_1*a_2*……*a_n时
欧拉定理
剩余系
一些超简单密码
维吉尼亚 密钥fox
凯撒(直接偏移)
凯特巴氏(颠倒字母表)
摩斯密码(字母对应电荷线)
希尔(hill)密码
一些攻击
RSA
求uf+vg=1
快速幂模m^e==?mod n
孙子定里
平方剩余
欧拉判责
勒让德符号
高斯二次互反率
雅可比符号
rabin公钥系统
原根和指数
t为a模m的指数,if:
a是模m的一个原根,if:
Elgmad公钥
抽象代数
同态基本定理
理想:
极大理想
对称密码
DES
AES
流密码
椭圆曲线密码
线性码,循环码,DSS,schnor签名,待续
基础
欧拉函数
欧拉函数φ(n)定义
定义为小于或等于n的正整数中与n互质的数的个数
计算方法的技巧
当a=a_1*a_2*……*a_n时
φ(a)=π(φ(ai))=π(a_i-1)
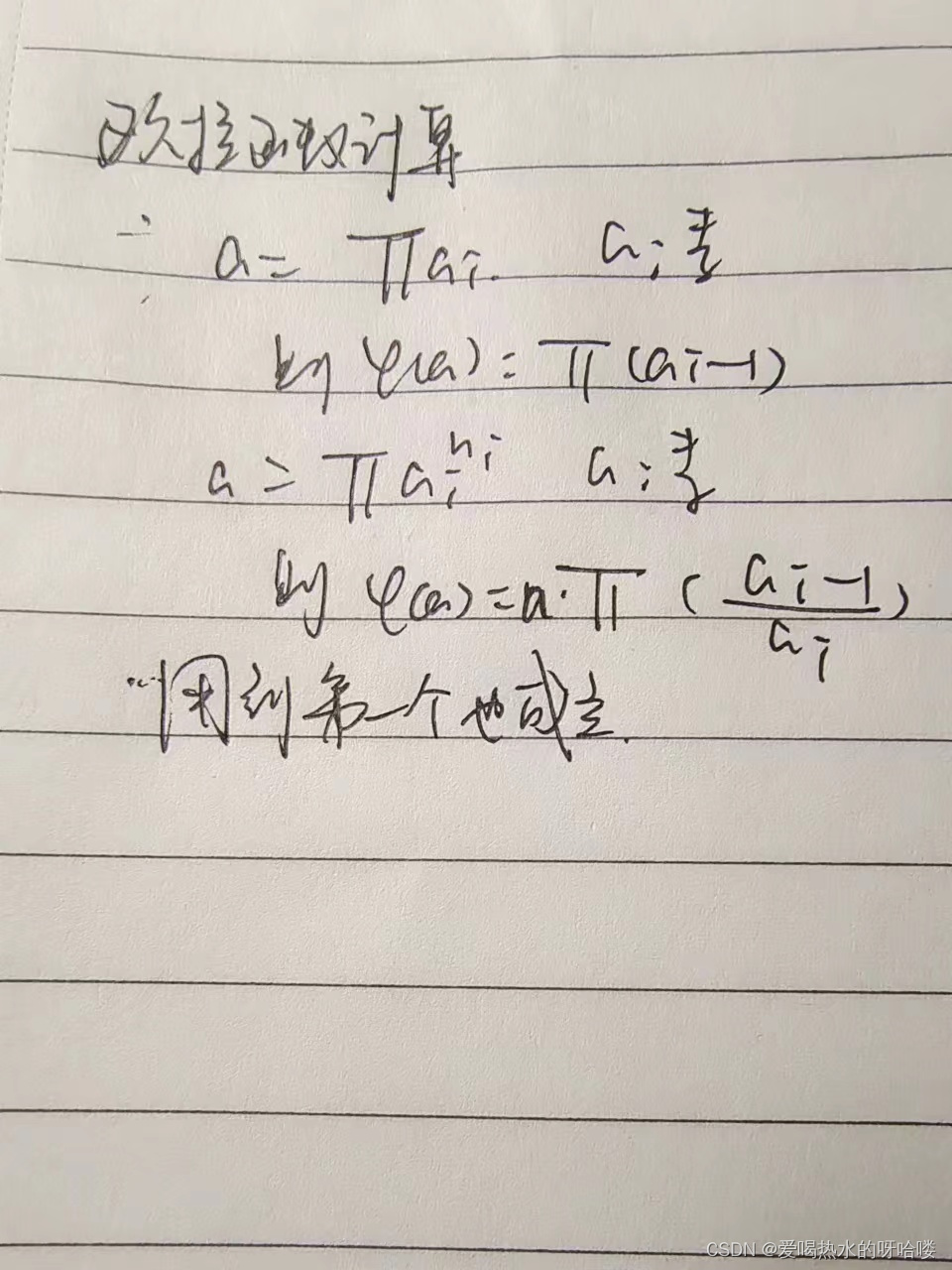
欧拉定理
(a,n)=1,则
剩余系
[a]类似于泛函与代数的等价类,所有mod n余a的数的集合
完全剩余系:每个剩余类去一个
简化剩余系:完全剩余类筛选出与n互质的
一些超简单密码
维吉尼亚 密钥fox
明文 flowerp
密钥+foxfoxf
密文=对应为相加
凯撒(直接偏移)
凯特巴氏(颠倒字母表)
摩斯密码(字母对应电荷线)
希尔(hill)密码
密钥矩阵K
C_i=KM_i
一些攻击
选择明文攻击(有加密机的访问权限)
选择密文攻击(有解密记得访问权限)
RSA
基于背包问题,若背包算法破解,就没用了。
原理:密钥生成、加密、解密


求uf+vg=1
可以用现成算法,也可以连分数(高代)
快速幂模m^e==?mod n
拆解指数(m**2)^(e/2)大概)奇数次数类似,-1
孙子定里
方程组
解法:M=πmi,Mi=M/mi
找MiMi'==1 mod mi
x=∑aiMiMi'
平方剩余
定义:a是模p平方剩余<=> x^2==a(modp) (*)有解
