LeetCode 算法:将有序数组转换为二叉搜索树 c++
原题链接🔗:将有序数组转换为二叉搜索树
难度:简单⭐️
题目
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树。
示例 1:
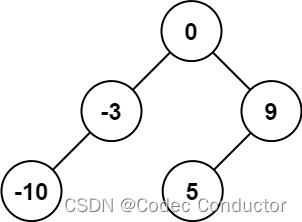
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
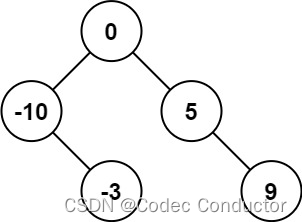
示例 2:
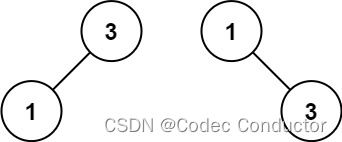
输入:nums = [1,3]
输出:[3,1]
解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
- 1 <= nums.length <= 104
- -104 <= nums[i] <= 104
- nums 按 严格递增 顺序排列
平衡二叉搜索树
-
平衡二叉搜索树(Balanced Binary Search Tree,简称BBST)是一种特殊的二叉搜索树,它在保持二叉搜索树的所有性质的同时,还保证了树的高度尽可能地小。这通常通过在插入和删除操作后重新平衡树来实现,以确保树的任何两个子树的高度差不会超过1。
-
平衡二叉搜索树的一个常见实现是AVL树,它是一种自平衡的二叉搜索树,其名称来源于其发明者Adelson-Velsky和Landis。AVL树在每次插入或删除操作后,都会进行必要的旋转操作来保持树的平衡。
-
AVL树的平衡操作包括四种基本的旋转:
- 左旋(Left Rotation):当节点的右子树比左子树高时,进行左旋来减少树的高度。
- 右旋(Right Rotation):当节点的左子树比右子树高时,进行右旋来减少树的高度。
- 左右旋(Left-Right Rotation):当节点的左子树的右子树比左子树高时,首先对左子树进行右旋,然后对节点进行左旋。
- 右左旋(Right-Left Rotation):当节点的右子树的左子树比右子树高时,首先对右子树进行左旋,然后对节点进行右旋。
-
AVL树的每个节点除了存储值和指向左右子节点的指针外,还存储了一个平衡因子(balance factor),通常是左子树高度和右子树高度的差值。节点的平衡因子只能是-1、0或1。
题解
递归法
- 解题思路:
将一个有序数组转换为二叉搜索树(BST)的解题思路基于二叉搜索树的性质:左子树上所有节点的值 < 根节点的值 < 右子树上所有节点的值。对于一个有序数组,我们可以利用数组的有序性来快速确定根节点和左右子树的划分点。
以下是解题步骤:
确定根节点:对于有序数组,中间元素(数组长度的一半)是一个很好的根节点候选,因为它可以很好地维持左右子树的大小平衡。
递归构建左右子树:使用数组下标来划分,左子树包含从数组开始到根节点前的部分,右子树包含从根节点的下一个元素到数组末尾的部分。
递归终止条件:当子数组为空时,返回null。
构建树:对于每个子数组,重复上述步骤,递归地构建左右子树。
返回根节点:递归结束时,返回构建的树的根节点。
下面是具体的算法逻辑:
- 定义一个递归函数
sortedArrayToBST,它接收有序数组的起始索引和结束索引作为参数。- 计算中间索引mid:
mid = (start+ end) / 2。- 使用mid索引处的值创建一个新的树节点。
- 递归地调用
sortedArrayToBST来构建左子树,使用start和mid - 1作为新的参数。- 递归地调用
sortedArrayToBST来构建右子树,使用mid + 1和end作为新的参数。- 将左子树和右子树分别赋值给新创建的根节点的左右子节点。
- 返回根节点。
-
复杂度:时间复杂度O(n),空间复杂度O(logn)。
-
c++ demo:
#include <iostream>
#include <vector>// 定义二叉树节点
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 将有序数组转换为二叉搜索树的函数
class Solution {
public:TreeNode* sortedArrayToBST(std::vector<int>& nums) {return sortedArrayToBSTHelper(nums, 0, nums.size() - 1);}private:TreeNode* sortedArrayToBSTHelper(std::vector<int>& nums, int start, int end) {if (start > end) {return nullptr;}// 选择中间的元素作为根节点int mid = start + (end - start) / 2;TreeNode* node = new TreeNode(nums[mid]);// 递归地构建左子树和右子树node->left = sortedArrayToBSTHelper(nums, start, mid - 1);node->right = sortedArrayToBSTHelper(nums, mid + 1, end);return node;}
};// 辅助函数:中序遍历二叉树并打印节点值
void inorderTraversal(TreeNode* node) {if (!node) return;inorderTraversal(node->left);std::cout << node->val << " ";inorderTraversal(node->right);
}// 辅助函数:释放二叉树内存
void deleteTree(TreeNode* node) {if (!node) return;deleteTree(node->left);deleteTree(node->right);delete node;
}int main() {// 创建Solution实例Solution solution;// 有序数组std::vector<int> nums = { -10, -3, 0, 5, 9 };// 将有序数组转换为BSTTreeNode* root = solution.sortedArrayToBST(nums);// 中序遍历BST并打印节点值std::cout << "Inorder traversal of the constructed BST:" << std::endl;inorderTraversal(root);std::cout << std::endl;// 释放二叉树内存deleteTree(root);return 0;
}
- 输出结果:
Inorder traversal of the constructed BST:
-10 -3 0 5 9
- demo 仓库地址:sortedArrayToBST
