决策树划分属性依据
划分依据
- 基尼系数
- 基尼系数的应用
- 信息熵
- 信息增益
- 信息增益的使用
- 信息增益准则的局限性
最近在学习项目的时候经常用到随机森林,所以对决策树进行探索学习。
基尼系数
基尼系数用来判断不确定性或不纯度,数值范围在0~0.5之间,数值越低,数据集越纯。
基尼系数的计算:
假设数据集有K个类别,类别K在数据集中出现的概率为Pk,则基尼系数为:
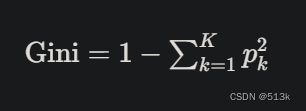
上式是用来求某个节点的基尼系数,要求某个属性的基尼系数用下面的公式:
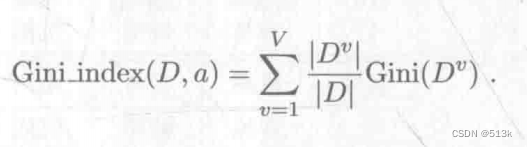
最后选择基尼系数最小的属性进行划分即可。
基尼系数的应用
在决策树中,假如某个节点的基尼系数就是0,此时被分类到这个节点的数据集是纯的,意思就是按照此叶节点的父节点的分类方法来说,此叶节点都是同一个类别的,不需要再次分裂决策。
信息熵
信息熵和基尼系数作用相同,都是用来度量样本集合纯度的指标。
计算方法:
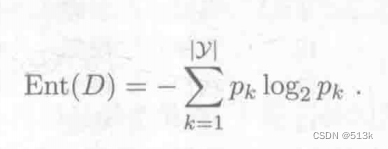
Pk是当前样本集合中第k类样本所占比例,Ent(D)(信息熵)越小,集合D的纯度越高。
这里约定当Pk为0时Ent(D)=0;
信息增益
计算公式: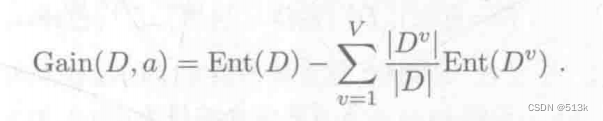
假设现在对集合D使用属性a来进行划分,属性a有v个取值,也就是有v个节点,上式中Dv是第v个节点就是取值为v的样本个数。
信息增益的使用
信息增益越大,说明使用属性a来划分所获得的纯度提升越大,决策树越好。
信息增益准则的局限性
从上面的公式可以看出,信息增益偏好可取值数目较多的属性,假如某个属性可取值达到了n,也就是每个样本都不一样,比如“编号”属性,那可以计算出这个属性的信息增益接近1,选择这样的属性来划分很可能不具有泛化能力。
改进:
使用增益率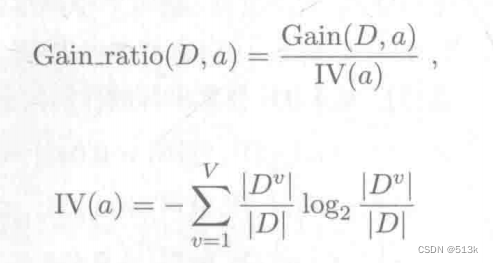
对于这个公式,当属性a的可取值越多时,则IV(a)会越大,增益率变小,进行了平衡。同样的,增益率准则也有局限,它对可取值较少的属性又有所偏好。
最终:先找出信息增益高于平均水平的属性,再从中选择增益率最高的即可。
