当前位置：首页 > news >正文

LeetCode 算法：翻转二叉树 c++

news 2025/7/28 0:49:37

原题链接🔗：翻转二叉树
难度：简单⭐️

题目

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：
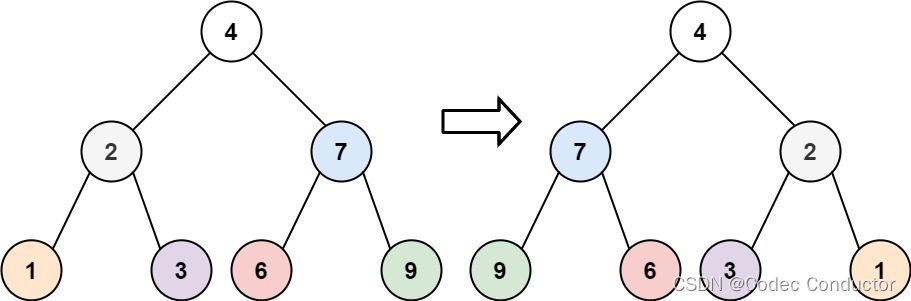
在这里插入图片描述
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：
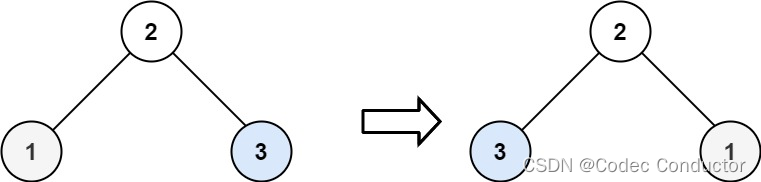
在这里插入图片描述

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：
输入：root = []
输出：[]

提示：

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

题解

递归法

解题思路: 翻转二叉树的解题思路主要基于递归和树的遍历。以下是详细的步骤和思路：

理解问题：首先，明确题目要求翻转二叉树，即将每个节点的左子树和右子树互换。

递归方法：递归是解决这个问题的自然选择，因为它可以很好地处理树结构的遍历。

递归终止条件：递归的基本终止条件是当节点为空时，不需要翻转，直接返回nullptr。

递归逻辑：

在递归到每个节点时，首先交换当前节点的左子树和右子树。
然后，递归地翻转当前节点的左子树（原来的右子树）。
接着，递归地翻转当前节点的右子树（原来的左子树）。

递归返回值：在递归调用结束后，返回当前节点。虽然在翻转操作中，我们关心的是操作本身而不是返回值，但递归需要返回值来构建翻转后的树结构。

编写递归函数：实现递归函数，使用条件语句来处理递归终止条件，并使用递归调用来翻转子树。

测试：使用不同的二叉树结构来测试你的翻转算法，确保它可以正确地翻转所有类型的树。

优化：考虑算法的时间复杂度和空间复杂度。翻转操作的时间复杂度是O(n)，其中n是树中的节点数，因为每个节点恰好被访问一次。空间复杂度是O(h)，其中h是树的高度，这是因为递归调用的深度。

边界条件：确保处理了所有边界条件，如空树或只有一个节点的树。

代码实现：将上述思路转化为代码实现。

复杂度：

时间复杂度是 O(N)，其中 N 为二叉树节点的数目。我们会遍历二叉树中的每一个节点，对每个节点而言，我们在常数时间内交换其两棵子树；
空间复杂度是 O(N)，使用的空间由递归栈的深度决定，它等于当前节点在二叉树中的高度。在平均情况下，二叉树的高度与节点个数为对数关系，即 O(log⁡N)。而在最坏情况下，树形成链状，空间复杂度为 O(N)。

c++ demo：

#include <iostream>
#include <queue>// 定义二叉树节点
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 翻转二叉树的解决方案
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (!root) return nullptr;  // 递归终止条件：如果节点为空，返回nullptrstd::swap(root->left, root->right);  // 交换当前节点的左右子树invertTree(root->left);             // 递归翻转左子树invertTree(root->right);            // 递归翻转右子树return root;                        // 返回翻转后的树的根节点}
};// 辅助函数：按层序遍历打印二叉树
void printLevelOrder(TreeNode* root) {if (!root) return;std::queue<TreeNode*> q;q.push(root);while (!q.empty()) {TreeNode* node = q.front();q.pop();if (node->left) q.push(node->left);if (node->right) q.push(node->right);std::cout << node->val << " ";}std::cout << std::endl;
}// 主函数
int main() {Solution solution;// 创建示例二叉树//       4//      / \//     2   7//    / \ / \//   1  3 6  9TreeNode* root = new TreeNode(4);root->left = new TreeNode(2);root->right = new TreeNode(7);root->left->left = new TreeNode(1);root->left->right = new TreeNode(3);root->right->left = new TreeNode(6);root->right->right = new TreeNode(9);std::cout << "Original binary tree:" << std::endl;printLevelOrder(root);// 翻转二叉树TreeNode* invertedRoot = solution.invertTree(root);std::cout << "Inverted binary tree:" << std::endl;printLevelOrder(invertedRoot);// 清理分配的内存delete root->left->left;delete root->left->right;delete root->left;delete root->right->left;delete root->right->right;delete root->right;delete root;return 0;
}