当前位置：首页 > news >正文

Atcoder Beginner Contest 359

news 2025/7/4 20:03:07

传送门

A - Count Takahashi

时间限制：2秒内存限制：1024MB

分数：100分

问题描述

给定 N 个字符串。

第 i 个字符串 $S_i$ ( $1 \le i \le N$ ) 要么是 Takahashi 要么是 Aoki。

有多少个 i 使得 $S_i$ 等于 Takahashi ？

限制

$1 \le N \le 100$
N 是整数。
每个字符串 $S_i$ 是 Takahashi 或者 Aoki。( $1 \le i \le N$ )

输入格式

$N\\ S_1\\ S_2\\ \vdots\\ S_N$

输出格式

输出 $S_i$ 等于 Takahashi 的数量。

样例输入输出

样例输入1

$3\\ Aoki\\ Takahashi\\ Takahashi$

样例输出1

$2$

$S_2$ 和 $S_3$ 等于 Takahashi，而 $S_1$ 不等于 Takahashi。

因此，输出 2。

样例输入2

$2\\ Aoki\\ Aoki$

样例输出2

$0$

没有 $S_i$ 等于 Takahashi。

样例输入3

$20\\ Aoki\\ Takahashi\\ Takahashi\\ Aoki\\ Aoki\\ Aoki\\ Aoki\\ Takahashi\\ Aoki\\ Aoki\\ Aoki\\ Takahashi\\ Takahashi\\ Aoki\\ Takahashi\\ Aoki\\ Aoki\\ Aoki\\ Aoki\\ Takahashi$

样例输出3

$7$

代码

#include <bits/stdc++.h>
using namespace std;inline int read() {int x = 0, f = 1; char c = getchar();while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();return x * f;
}int main () {int n = read(), cnt = 0;while (n--) {string s;cin >> s;if (s[0] == 'T') cnt++;}cout << cnt;return 0;
}

B - Couples

时间限制：2秒内存限制：1024MB

分数：150分

问题描述

有 2N 个人站成一排，位于第i个位置的人穿着颜色为 $A_i$ 的衣服。这里，衣服有 N 种颜色，每种颜色正好有两个人穿。

找出满足以下条件的整数 $i = 1, 2, \cdots, N$ 的数量：

颜色为 i 的两个人之间正好有一个人。

限制

$2 \le N \le 100$
$1 \le A_i \le N$
每个从 1 到 N 的每个整数在 A 中恰好出现两次。
所有输入值都是整数。

输入格式

$N\\ A_1 \hspace{1em} A_2 \hspace{1em} \cdots \hspace{1em} A_{2N}$

输出格式

输出答案

样例输入输出

样例输入1

$3\\ 1 \hspace{0.5em} 2 \hspace{0.5em} 1 \hspace{0.5em} 3 \hspace{0.5em} 2 \hspace{0.5em} 3$

样例输出1

$2$

有两个 i 值满足条件：1 和 3。

实际上，穿着颜色为 1 的衣服的人分别在从左数第 1 和第 3 的位置，中间正好有一个人。

样例输入2

$2\\ 1 \hspace{0.5em} 1 \hspace{0.5em} 2 \hspace{0.5em} 2$

样例输出2

$0$

没有 i 值满足条件。

样例输入3

$4\\ 4 \hspace{0.5em} 3 \hspace{0.5em} 2 \hspace{0.5em} 3 \hspace{0.5em} 2 \hspace{0.5em} 1 \hspace{0.5em} 4 \hspace{0.5em} 1$

样例输出3

$3$

代码

#include <bits/stdc++.h>
using namespace std;inline int read() {int x = 0, f = 1; char c = getchar();while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();return x * f;
}int main () {int n = read(), a[205], cnt = 0;for (int i = 1; i <= 2 * n; i++) a[i] = read();for (int i = 1; i < 2 * n; i++) {for (int j = i + 1; j <= 2 * n; j++) {if (a[i] == a[j] && j == i + 2) {cnt++;break;}}}cout << cnt;return 0;
}

C - Tile Distance 2

时间限制：2秒内存限制：1024MB

分数：350分

问题描述

坐标平面被 2 × 1 的瓷砖覆盖。瓷砖的铺设遵循以下规则：

对于整数对 (i, j)，方块 $A_{i, j} = \{(x, y) | i \le x \le i + 1 \land j \le y \le j + 1\}$ 包含在一块瓷砖中。
当 i + j 是偶数时， $A_{i ,j}$ 和 $A_{i + 1, j}$ 包含在同一块瓷砖中。

瓷砖包括它们的边界，并且没有两块不同的瓷砖共享正面积。

在靠近原点的地方，瓷砖的铺设如下：

Takahashi 从坐标平面上的点 ( $S_x$ + 0.5, $S_y$ + 0.5) 开始。

他可以重复以下移动操作任意次数：

选择一个方向（上，下，左，右）和一个正整数 n。向该方向移动 n 个单位。
每次他进入一个瓷砖，他需要支付 1 的费用。

求他到达点 ( $T_x$ + 0.5, $T_y$ + 0.5) 所需支付的最少费用。

限制

$0 \le S_x \le 2 \times 10^{16}$
$0 \le S_y \le 2 \times 10^{16}$
$0 \le T_x \le 2 \times 10^{16}$
$0 \le T_y \le 2 \times 10^{16}$
所有输入都是整数。

输入格式

$S_x \hspace{1em} S_y\\ T_x \hspace{1em} T_y$

输出格式

输出 Takahashi 需要支付的最少费用。

样例输入输出

样例输入1

$5 \hspace{0.5em} 0\\ 2 \hspace{0.5em} 5$

样例输出1

$5$

例如，Takahashi 可以通过以下移动支付 5 的费用：

向左移动 1。支付 0 的费用。
向上移动 1。支付 1 的费用。
向左移动 1。支付 0 的费用。
向上移动 3。支付 3 的费用。
向左移动 1。支付 0 的费用。
向上移动 1。支付 1 的费用。

无法将费用减少到 4 或更少，因此输出 5。

样例输入2

$3 \hspace{0.5em} 1\\ 4 \hspace{0.5em} 1$

样例输出2

$0$

有些情况下不需要支付任何费用。

样例输入3

$2552608206527595 \hspace{0.5em} 5411232866732612\\ 771856005518028 \hspace{0.5em} 7206210729152763$

样例输出3

$1794977862420151$

注意，输出的值可能会超过 32 位整数的范围。

思路

将移动分为竖直方向跟水平方向来考虑。

任何情况下，在竖直方向上的移动需要支付 $|S_y - T_y|$ 。与此同时也能在水平方向上移动 $|S_y - T_y|$ 个单位，所以要给 $S_x$ 加上 $|S_y - T_y|$ 。如果在此之后水平方向依旧无法到达，则需要加上 $\frac{|S_x - T_x|}{2}$ 。

代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
signed main () {int a, b, c, d;cin >> a >> b >> c >> d;if (a > c) swap(a, c), swap(b, d);if ((c + d) & 1) c--;if ((a + b) % 2 == 0) a++;int ans = abs(b - d);a += ans;if (a < c) ans += (c - a + 1) / 2;cout << ans;return 0;
}

E - Water Tank

时间限制：2秒内存限制：1024MB

分数：500分

问题描述

给定一个长度为 N 的正整数序列 $H = (H_1, H_2, \cdots, H_N)$ 。

有一个长度为 N + 1 的非负整数序列 $A = (A_1, A_2, \cdots, A_N)$ ，初始时 $A_1 = A_2 = \cdots = A_N = 0$ 。

重复执行以下操作直到结束：

1. 将 $A_0$ 的值增加 1。
2. 对于每个 $1, 2, \cdots, N$ ，按顺序执行以下操作：
如果 $A_{i - 1} > A_i$ 并且 $A_{i - 1} > H_i$ ，则将 $A_{i - 1}$ 的值减少 1，同时将 $A_i$ 的值增加 1。

对于每个 $i = 1, 2, \cdots, N$ ，找出在 $A_i > 0$ 首次成立之前执行了多少次操作。

限制

$1 \le N \le 2 \times 10 ^5$
$1 \le H_i \le 10^9 \hspace{0.5em} (1 \le i \le N)$
所有输入都是整数。

输入格式

$N\\ H_1 \hspace{1em} H_2 \hspace{1em} \ldots \hspace{1em} H_N$

输出格式

将对于每个 $i = 1, 2, \ldots, N$ 的答案输出在一行上，以空格分隔。

样例输入输出

样例输入1

$5\\ 3 \hspace{0.5em} 1 \hspace{0.5em} 4 \hspace{0.5em} 1 \hspace{0.5em} 5$

样例输出1

$4 \hspace{0.5em} 5 \hspace{0.5em} 13 \hspace{0.5em} 14 \hspace{0.5em} 26$

前五次操作如下。

这里，每一行对应一次操作，最左边的列代表步骤 1，其余的代表步骤 2。

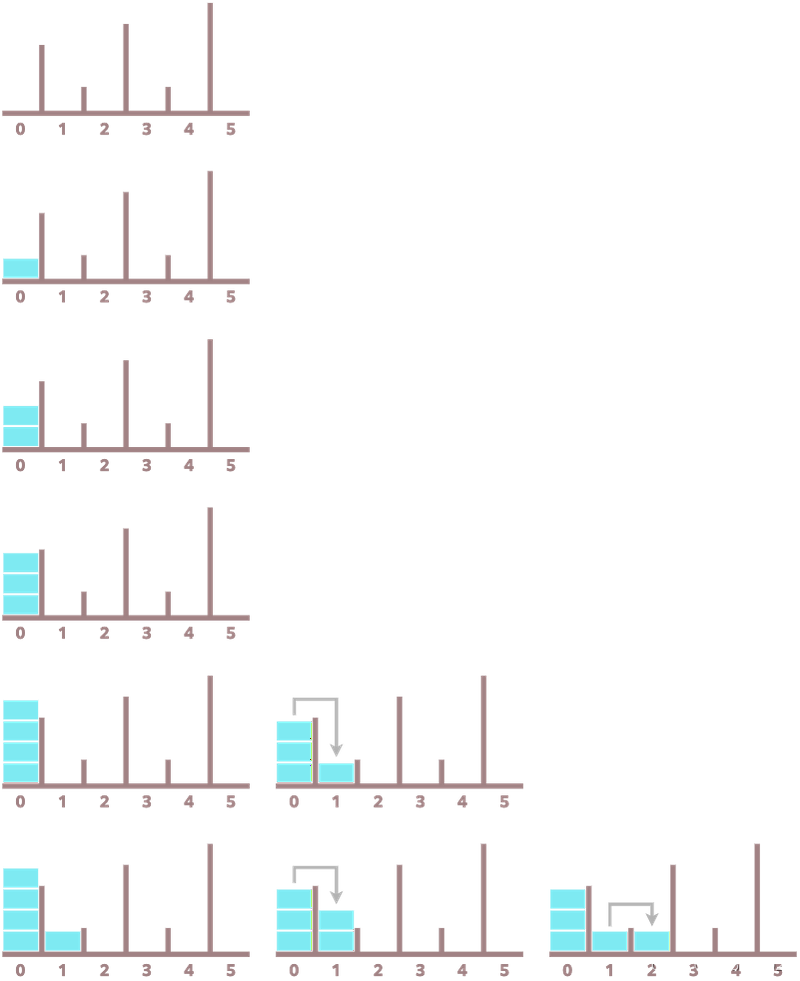
从这个图表中可以看出， $A_1 > 0$ 首次在第4次操作后成立，而 $A_2 > 0$ 首次在第5次操作后成立。

类似地， $A_3, A_4, A_5$ 的答案分别是 13，14，26。

因此，你应该输出 4 5 13 14 26。

样例输入2

$6\\ 1000000000 \hspace{0.5em} 1000000000 \hspace{0.5em} 1000000000 \hspace{0.5em} 1000000000 \hspace{0.5em} 1000000000 \hspace{0.5em} 1000000000$

样例输出2

$1000000001 \hspace{0.5em} 2000000001 \hspace{0.5em} 3000000001 \hspace{0.5em} 4000000001 \hspace{0.5em} 5000000001 \hspace{0.5em} 6000000001$

请注意，输出的值可能超出 32 位整数的范围。

样例输入3

$15\\ 748 \hspace{0.5em} 169 \hspace{0.5em} 586 \hspace{0.5em} 329 \hspace{0.5em} 972 \hspace{0.5em} 529 \hspace{0.5em} 432 \hspace{0.5em} 519 \hspace{0.5em} 408 \hspace{0.5em} 587 \hspace{0.5em} 138 \hspace{0.5em} 249 \hspace{0.5em} 656 \hspace{0.5em} 114 \hspace{0.5em} 632$

样例输出3

$749 \hspace{0.5em} 918 \hspace{0.5em} 1921 \hspace{0.5em} 2250 \hspace{0.5em} 4861 \hspace{0.5em} 5390 \hspace{0.5em} 5822 \hspace{0.5em} 6428 \hspace{0.5em} 6836 \hspace{0.5em} 7796 \hspace{0.5em} 7934 \hspace{0.5em} 8294 \hspace{0.5em} 10109 \hspace{0.5em} 10223 \hspace{0.5em} 11373$

思路

~~先说歪解：看样例猜答案~~

我们很容易能发现每一个输出第第一项都是 $A_1 = H_1 + 1$ 。当 $i > 1$ 的时候，如果 $H_{i - 1} \le H_i$ ，那么 $A_i = A_{i - 1} + H_{i}$ ；否则 $A_i = \sum_{j = 1}^{i - 1}max(A_j, H_i)$ 。

（至于为什么各位先别急

$A_1 = H_1 + 1$ 是因为 $A_0 > H_1$ 才能将大于 $H_1$ 的部分转移到 $A_1$ 上

每次操作第二步的转移，题目意思是从 $A_0$ 上连续转移到最右边可以转移的位置上，但这个也等价于在任意 $A_i$ 上加 1，再向右转移

如果 $H_{i - 1} \le H_i$ ，那么在这个条件下，只需要在 $A_{i - 1}$ 上加 1，再将这个 1 转移到 $A_i$ 上去即可（1步操作），所以 $A_i = A_{i - 1} + H_{i}$ 。

代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 10;
int n, h[N], a[N], maxid = 1;
inline int read() {int x = 0, f = 1; char c = getchar();while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();return x * f;
}
stack<int> s;
signed main () {n = read();for (int i = 1; i <= n; i++) h[i] = read();for (int i = 1; i <= n; i++) {while (s.size() && h[s.top()] < h[i]) s.pop();if (s.size()) a[i] = a[s.top()] + (i - s.top()) * h[i];else a[i] = i * h[i] + 1;s.push(i);}for (int i = 1; i <= n; i++) printf("%lld ", a[i]);return 0;
}

F - Tree Degree Optimization

时间限制：2秒内存限制：1024MB

分数：550分

问题描述

你有一个整数序列 $A = (A_1, A_2, \ldots, A_N)$ 。对于一棵有 N 个顶点的树 T，定义函数 f(T) 如下：

令 $d_i$ 为顶点 i 在树 T 中的度数。那么 $f(T) = \sum_{i = 1}^{N}d_i^2A_i$ 。

找出 f(T) 的最小可能值。

约束条件保证答案小于 $2^{63}$ 。

限制

$2 \le N \le 2 \times 10^5$
$1 \le A_i \le 10^9$
所有输入都是整数。

输入格式

$N\\ A_1 \hspace{1em} A_2 \hspace{1em} \ldots \hspace{1em} A_N$

输出格式

输出答案

样例输入输出

样例输入1

$4\\ 3 \hspace{0.5em} 2 \hspace{0.5em} 5 \hspace{0.5em} 2$

样例输出1

$24$

考虑一棵树 T，一条边连接顶点 1 和顶点 2，一条边连接顶点 2 和顶点 4，一条边连接顶点 4 和顶点 3。

那么， $f(T) = 1^2 \times 3 + 2^2 \times 2 + 1^2 \times 5 + 2^2 \times 2 = 24$ 。可以证明这是 f(T) 的最小值。

样例输入2

$3\\ 4 \hspace{0.5em} 3 \hspace{0.5em} 2$

样例输出2

$15$

样例输入3

$7\\ 10 \hspace{0.5em} 5 \hspace{0.5em} 10 \hspace{0.5em} 2 \hspace{0.5em} 10 \hspace{0.5em} 13 \hspace{0.5em} 15$

样例输出3

$128$

思路

由于是一棵树，所以树中总共有 N - 1 条边，那么每个节点的度的范围为 $[1, N - 1]$ ，每个节点的度的和 $\sum_{i = 1}^{N}d_i = 2N - 2$ 。

最开始的时候，把每个节点的度初始化为 1。接着再用一个优先队列维护每一个节点的度加一后，f(T) 增加的最小值。因为 $(d_i + 1)^2 = d_i^2 + 2 d_i + 1$ ，所以只需要把 $A_i(2d_i + 1)$ 放入优先队列，在维护一个小根堆即可。

代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 10;
int n, a[N], d[N], ans = 0LL;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
inline int read() {int x = 0, f = 1; char c = getchar();while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();return x * f;
}
signed main () {n = read();for (int i = 1; i <= n; i++) a[i] = read();for (int i = 1; i <= n; i++) {d[i] = 1, ans += a[i];q.push({3 * a[i], i});}for (int i = 1; i <= n - 2; i++) {int x = q.top().first, y = q.top().second;q.pop();ans += a[y] * (2 * d[y] + 1);d[y]++;q.push({a[y] * (2 * d[y] + 1), y});}printf("%lld", ans);return 0;
}

查看全文

http://www.lryc.cn/news/385031.html