刷代码随想录有感(119):动态规划——打家劫舍III(树形dp)
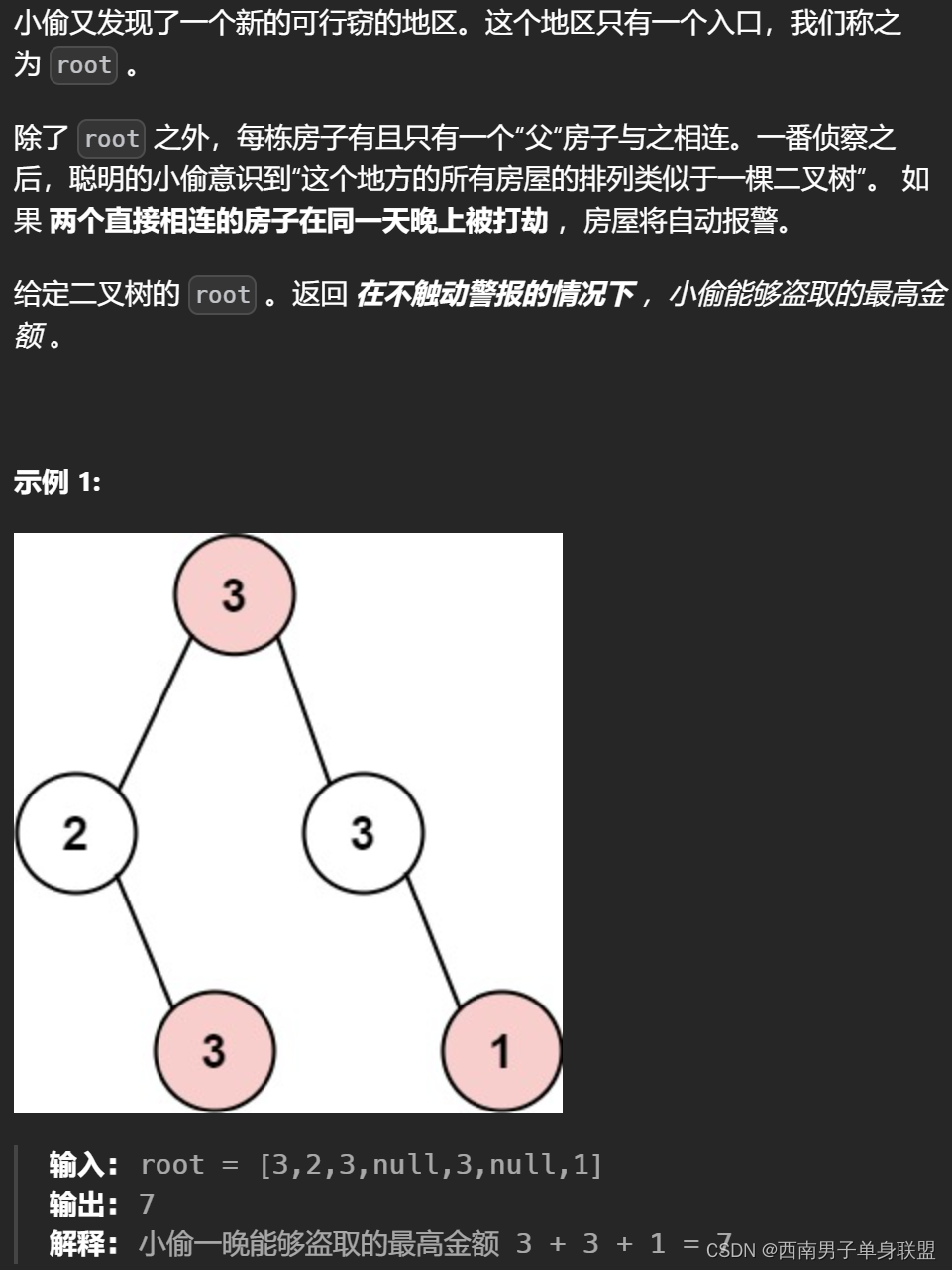
题干:
代码:
class Solution {
public:vector<int>dp(TreeNode* cur){if(cur == NULL)return vector<int>{0, 0};vector<int> left = dp(cur -> left);vector<int> right = dp(cur -> right);//偷int val1 = cur -> val + left[0] + right[0];//不偷int val2 = max(left[0], left[1]) + max(right[0], right[1]);return {val2, val1}; }int rob(TreeNode* root) {vector<int>res = dp(root);return max(res[0], res[1]);}
};使用一个长度为2的数组,记录当前节点偷与不偷所得到的的最大金钱。
dp数组以及下标的含义:下标为0记录不偷该节点所得到的的最大金钱,下标为1记录偷该节点所得到的的最大金钱。
递归顺序采用后序,即左-右-中,从下往上推。
