二叉树第一期:树与二叉树的概念
一、树
1.树的定义
与线性表不同,树是一种非线性的数据结构,由N(N>=0)个结点组成的具有层次关系的集合;因其形状类似生活中一颗倒挂着的树,故将其数据结构称为树。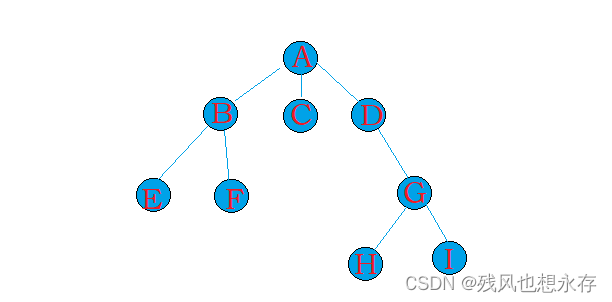
2.树的相关概念
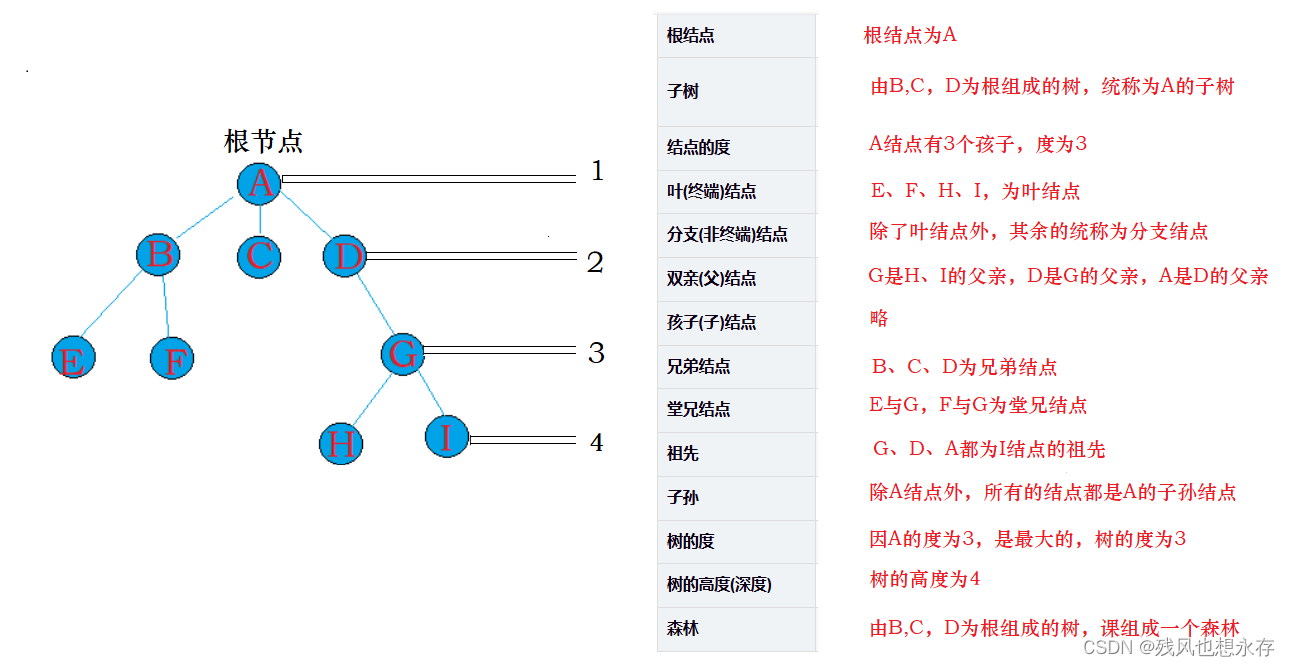
| 根结点 | 没有前驱的结点,称为根结点 |
|---|---|
| 子树 | 以某个结点为根结点的所有后代结点(包括此结点),为该结点的子树,例如B、E、F组成的树,是A的子树 |
| 结点的度 | 某个结点后继结点的个数,称为结点的度 |
| 叶(终端)结点 | 某个结点后继结点的个数为0,称为叶结点 |
| 分支(非终端)结点 | 某个结点后继结点的个数非0,称为分支结点 |
| 双亲(父)结点 | 某个结点的前驱结点,称为该结点的双亲结点 |
| 孩子(子)结点 | 某个结点的后继结点,称为该结点的孩子结点 |
| 兄弟结点 | 某两个结点的前驱结点相同,则称为兄弟结点 |
| 堂兄结点 | 某两个结点在同一个层次上,称为,堂兄结点 |
| 祖先 | 某个结点到根结点的一条路线上的结点,统称为该结点的祖先 |
| 子孙 | 某个结点的所有后代结点,统称为该结点的子孙 |
| 树的度 | 最大的结点的度,称为树的度 |
| 树的高度(深度) | 根结点到叶结点,所经过结点的个数,最大的,称为树的高度,或深度 |
| 结点的层级 | 某结点与根结点连线,所含义的结点个数 |
| 森林 | M(M>=2)个互不相交的树,称为森林 |
总结:
- 一个树,其任意子树是互不相交的,否则就不叫树,而是图,这一树形结构,如B、C、D为根组成的树,不存在相交情况。
- 任意一个树都可以看成根和子树,子树又可以看成,根和子树,所以树这一结构,是由递归搭建的。
3.树的表示
对树这一结构,有明确的了解后,又有一个新的问题,我们该如何的去表示的树的结构呢?常见的有孩子表示法,双亲表示法,孩子双亲表示法,孩子兄弟表示法;这里将介绍最好理解的孩子表示法,和优点明显的孩子兄弟表示法
i.孩子表示法
#define MAX 10 // 已知树的最大的深度typedef int TDatetype;typedef struct Tree
{TDatetype date;struct Tree* child[MAX];
}Tree;ii.左孩子右兄弟表示法
typedef int TDatetype;typedef struct Tree
{TDatetype date;struct Tree* child;struct Tree* brother;
}Tree;4.树的实际应用
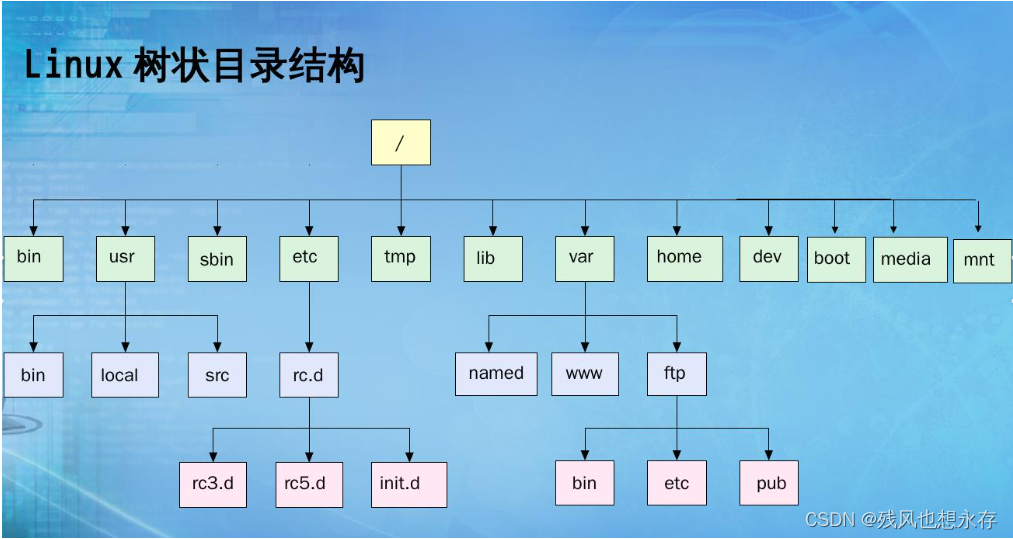
我们文件的存储方式就是以树这一结构存储,每一个盘即为一个树,所有盘则组成一个森林,下面则是Linux系统下,文件的存储结构。
二、二叉树
1.二叉树的定义
在树的定义基础上,树的度最大不超过2的(每个结点的度最大不超过2的),即为二叉树。(注:二叉树有左孩子右孩子之分)
2.特殊的二叉树
i.满二叉树
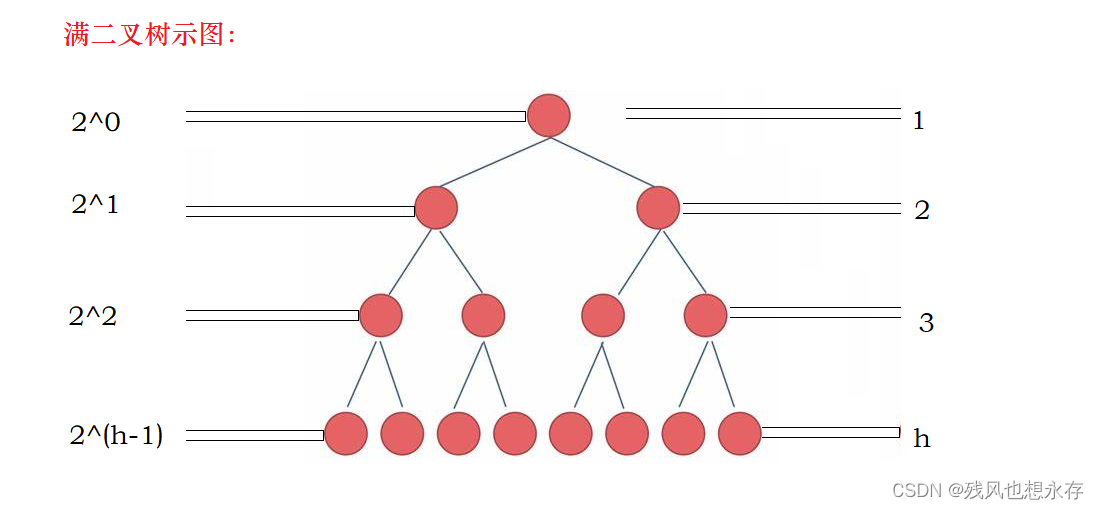
满二叉树的定义:树的深度为h,每一层都达到含有结点的最大个数,即第x(0<x<=h)层,结点个数 = 2^(x-1);
ii.完成二叉树
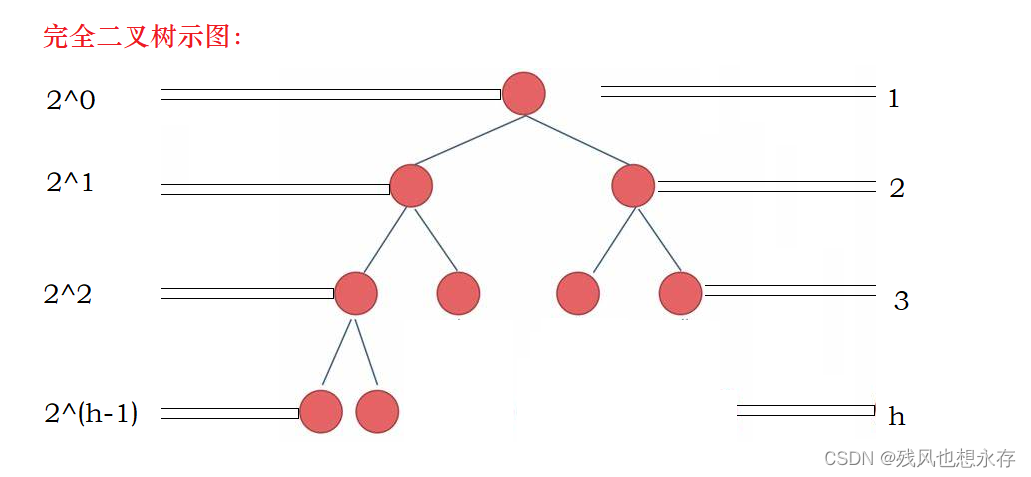
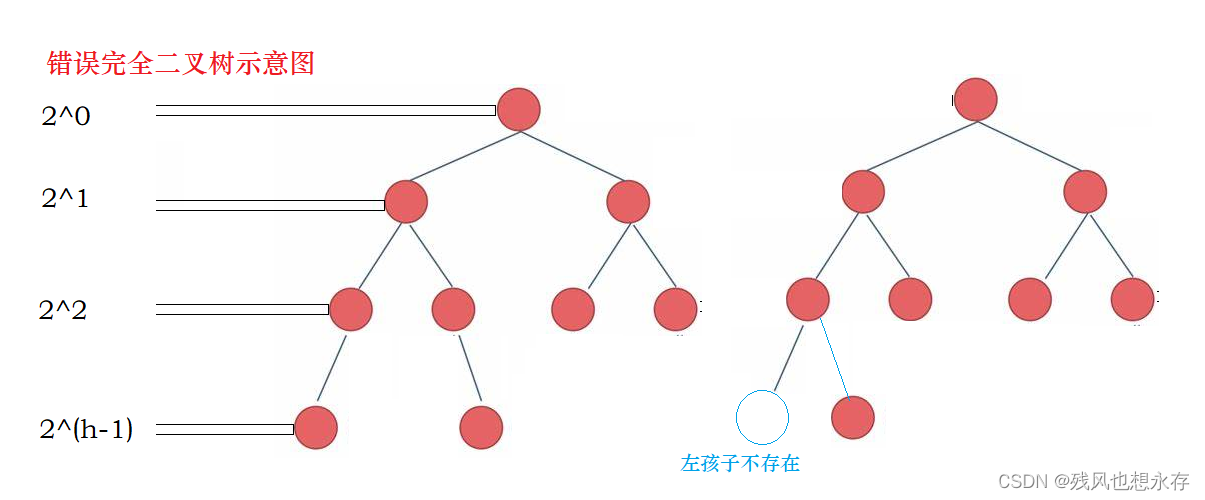
完全二叉树的定义:树的深度为h,前h-1层,结点个数达到最大值,第h层,从左到右有连续的结点。
3.二叉树的性质
- 第H层结点个数:2^(H-1)
- 高度为H的二叉树,所含有结点个数的最大值为2^H-1
- N个结点的满二叉树,其高度为以2为底,log(N+1)
- N个结点的完全二叉树,其高度为以2为底,log(N+X+1),X为相同高度的满二叉树与完全二叉树的结点个数差的绝对值
- 终端结点的个数 = 度为2的结点个数 + 1
4.二叉树的表示
i.二叉树的顺序结构
二叉树的顺序结构:将一颗二叉树的数据,以层为顺序,依次存储在数组中(保留空结点的位置)。
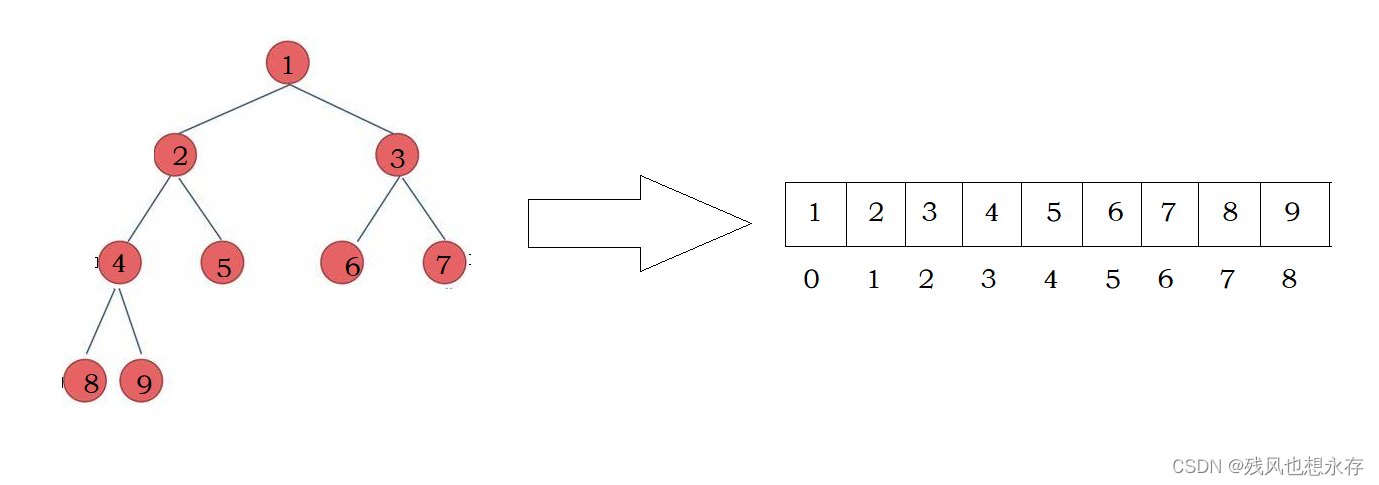
typedef int BTDateType; // 重定义树的数据类型typedef struct BinaryTree
{BTDateType* date; // 动态顺序表int size; // 当前顺序表存储数据的个数int capacity; // 当前顺序表的容量大小
}BinaryTree;
为什么要这么设计呢?
因为我们通过数组下标,可以得出其父亲或者两个孩子的结点位置;
- 某结点左孩子的下标 = 该结点的下标 * 2 + 1
- 某结点右孩子的下标 = 该结点的下标 * 2 + 2
- 某结点的父亲下标 = (该结点的下标 - 1) / 2
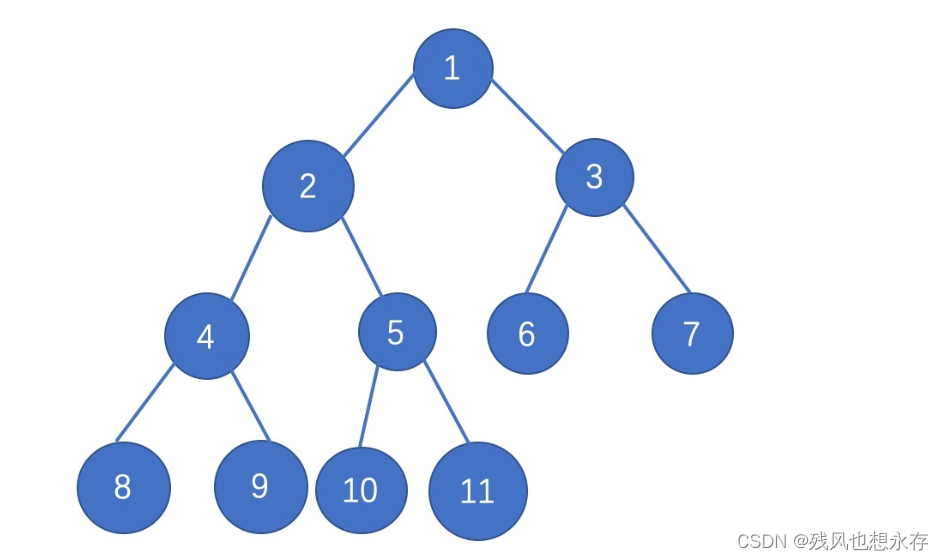
读者,若不相信,可以以上面示图为例子,代入数据,进行自我验证!!!
- 根据此特性,
- 首先:我们就可以理解了,为什么要留着空结点的位置,而不是直接把数据依次存入~
- 最后:可以得出结论适合于存储完全二叉树,而不适合存储普通二叉树,因为普通二叉树,会造成大量的空间浪费。
ii.二叉树的链式结构
二叉树的链式结构,声明如下:孩子不存在,则用NULL表示;
typedef int BTDatetype;typedef struct BinaryTree
{BTDatetype date; // 数据struct Tree* lift; // 左孩子struct Tree* right; // 右孩子
}BT;