【数据结构与算法】最小生成树,Prim算法,Kruskal算法 详解
最小生成树的实际应用背景。
最节省经费的前提下,在n个城市之间建立通信联络网。
Kruskal算法(基于并查集)
void init() {for (int i = 1; i <= n; i++) {pre[i] = i;}
}ll root(ll a) {ll i = a;while (pre[i] != i) {i = pre[i];}return i = pre[i];
}bool merge(ll a, ll b) {ll ra = root(a);ll rb = root(b);if (ra == rb) {return 0;}pre[ra] = rb;return 1;
}ll kruskal() {sort(edge.begin(), edge.end());init();ll sum = 0;ll cnt = 0;for (const auto e : edge) {if (merge(e.u, e.v)) {sum += e.w;cnt++;}}return sum;
}
什么图适合用Prim算法求最小生成树,什么图适合用Kruskal算法求最小生成树。
-
Prim算法:归并顶点,与边数无关,适合于稠密图,即边的数量接近于节点数量的平方。Prim算法从一个节点开始,每次都添加一条连接已选节点和未选节点的最小边,因此它更适合于边的数量较多的情况。
-
Kruskal算法:归并边,适合于稀疏图,即边的数量远小于节点数量的平方。Kruskal算法每次都添加一条当前最小的边,只要这条边不会形成环,因此它更适合于边的数量较少的情况。
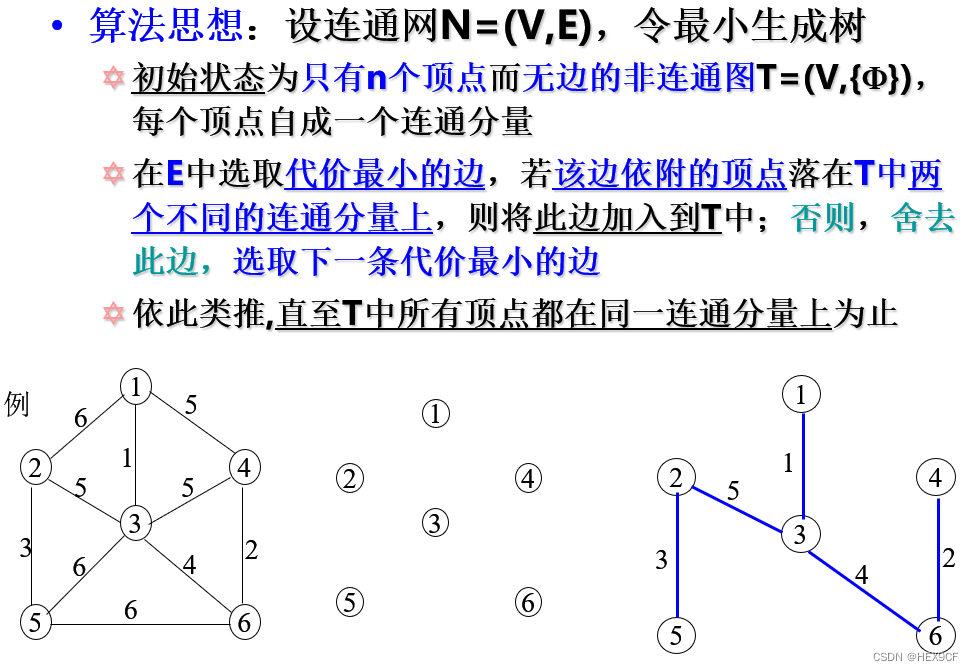
图示用Prim算法及Kruskal算法求最小生成树的过程。
-
Prim算法:

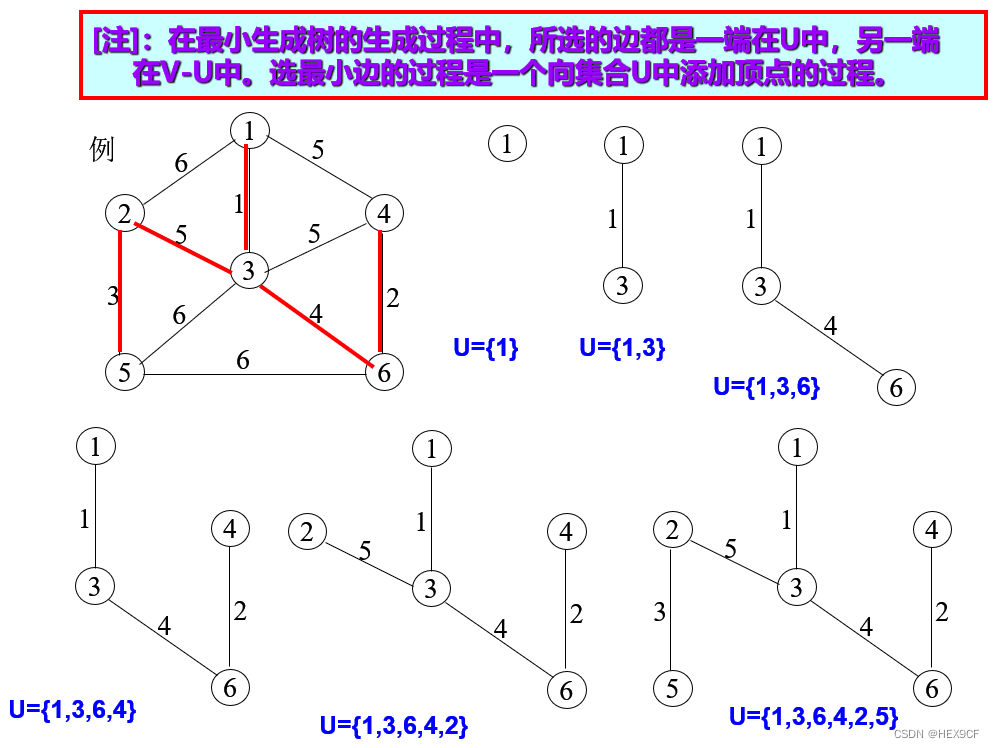
-
Kruskal算法: