【考研408计算机组成原理】数值表示和运算之快速数值转换

苏泽
“弃工从研”的路上很孤独,于是我记下了些许笔记相伴,希望能够帮助到大家
另外,利用了工作之余的一点点时间,整理了一套考研408的知识图谱,
我根据这一套知识图谱打造了这样一个408知识图谱问答系统
里面的每一个回答都是根据考研408的考点回复的

目前暂时只接入了微信,如果大家对这个问答系统感兴趣的话可以在我的主页里找到我的微信号
找我拉进测试群免费体验哦
这一章希望分享一份快速数值转换的技巧笔记
目录
这一章希望分享一份快速数值转换的技巧笔记
数值转换的几个方向
进制转换
这里我们可以观察这个表发现一个规律,那就是所有十六进制的每一位都能够用 二进制的四位来表示
各种“码”的转换
关于原码、反码、补码以及移码的转换,以下是整理的要点:
其中原码转补码的小技巧
考研易错点难点:浮点数
先说浮点数的定义
☆求补运算的使用
数值转换的几个方向
进制转换
首先考研只会考到2进制 10进制 和16进制的转换 所以对于这些数值之间的表示和不同进制之间的转换就成为了一项必备技能
而这些进制的转换相信大家都不陌生 通过辗转相除法之类的计算方法就能计算得出, 但我这里要记录的 是一种能够通过少量记忆 达到免除计算 节省时间的一种方法
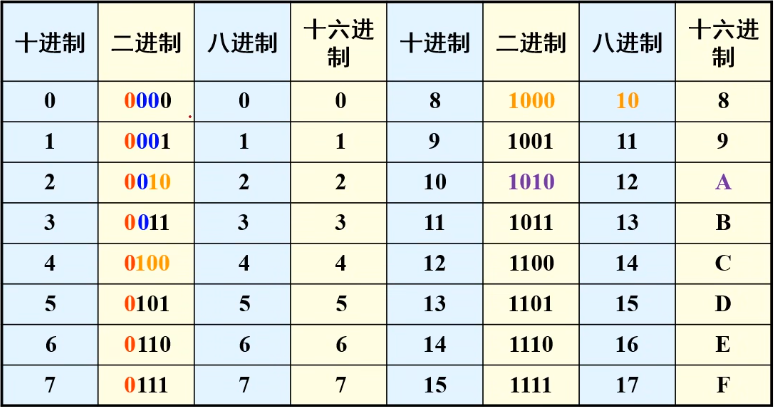
首先我们可以看到这样一个表 这个表并不稀奇 大家也能自己去算一下 也不需要背考试的时候
其实只需要把16进制当中的A~F对应的十进制数给写到草稿纸上即可
A~F分别对应的是10~15
这里我们可以观察这个表发现一个规律,那就是所有十六进制的每一位都能够用 二进制的四位来表示
用下面这个例子快速掌握这个小技巧

这里要求16进制转2进制
那么现在问题就变成了“3”如何用4位二进制表示,是不是2的1次方+2的0次方,所以是0011
B是11 =8+0+2+1 所以是1011
...以此类推
这样我们把每一位转成二进制的数 都写到纸上 然后按顺序拼起来就是结果了
就不需要用传统方法模16那种方法 无需计算快速得出结果
各种“码”的转换
再到经典的原、反、补、移码了
先看这张整理好的图
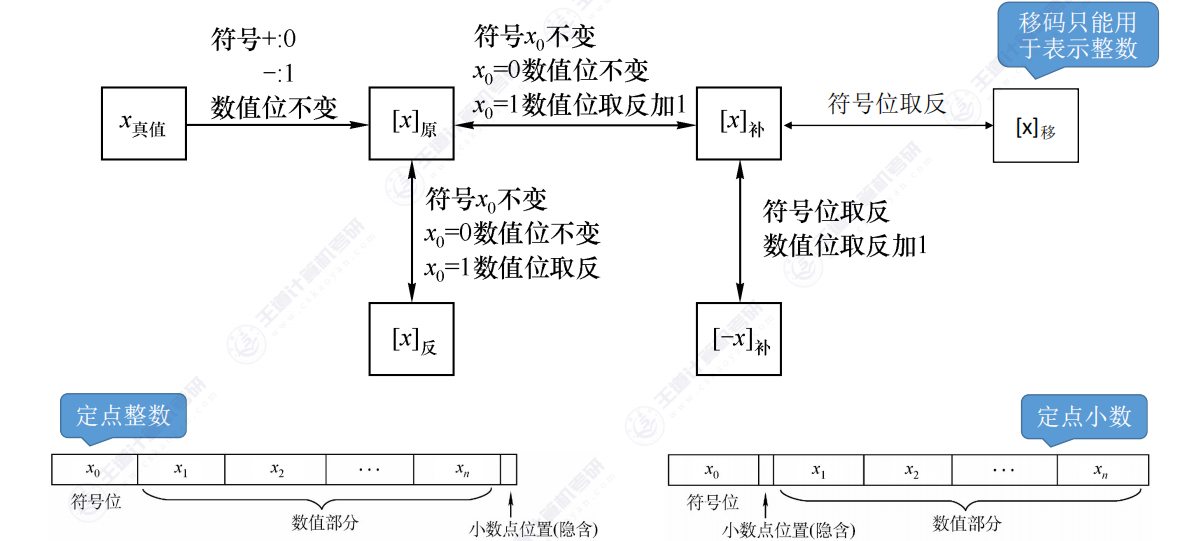
关于原码、反码、补码以及移码的转换,以下是整理的要点:
-
原码:
- 原码是最直接的表示方式,最高位是符号位,0代表正数,1代表负数。其余位表示数值的大小。
-
反码:
- 正数的反码与其原码相同。
- 负数的反码是将其原码除符号位外的所有位取反。
-
补码:
- 正数的补码与其原码相同。
- 负数的补码是其反码加1。
-
移码:
- 移码是补码的一种变体,其符号位取反。这使得正数的移码比补码大1,而负数的移码比补码小1。
其中原码转补码的小技巧
这里有个小技巧 王道里面也说过的:符号位不变,从左往右数第一个“1” ,它的左边全取反 右边保留原样
这个技巧能够其他转换当中的完美等价“数值位取反加1”这一条件
考研易错点难点:浮点数
先说浮点数的定义
之所以“浮” 是因为他的小数点 飘忽不定 例如1.01 可以写成10.1*10^-1
所以计算机当中需要一个统一的标准 将这些小数给统一起来 就有了下面的部分 来介绍计算机是如何统一的表示浮点数的
-
浮点数的组成:
- 浮点数通常由三部分组成:阶码(Exponent)、尾数(Mantissa)和符号位(Sign)。

关于浮点数移位的解释 和记忆的口诀
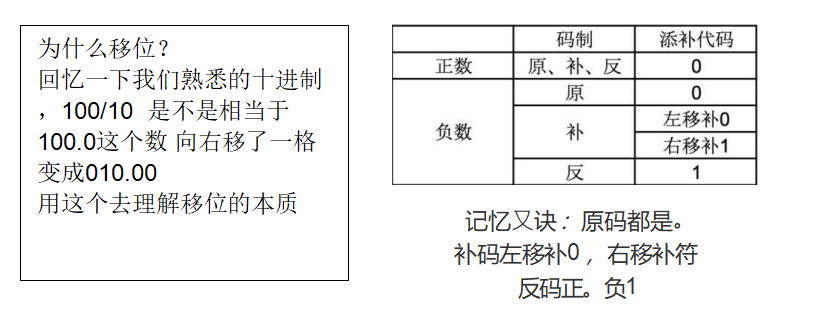
逻辑移位: 将操作数视为⽆符号 ,⼀律补0
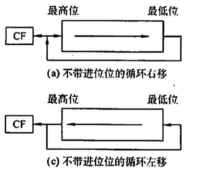
循环移位: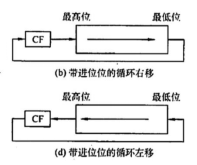
☆求补运算的使用
负16进制->补码 (快速)
原码
正数补码=原码,所以不多说
负数2进制补码: ⽤常归⽅法即可
负数16进制补码: 求补运算,说⽩了就是求这个数的⼀个互补值,使得这个数最高位能够进1位且其他位都为 0,这种运算就称之为“求补运算 ”
例 :求带符 号补 码FCA358H的 真值?
使用求补运算相当求让FCA358H加上一个数使其=10000000H
FCA358H+035CA8H= 10000000H
此时我们求出来的是FCA358H的补数,由于FCA358H显然是负数, 所以在转为真值的时候 一 定要记得加上负号! !
同时,将有符号补数转为原码时也要保持符号一致性,所以最后FCA358H的原码为: 835CA8H
1000H-002BH =FFD5H
