机器学习——决策树
决策树
决策树可以理解为是一颗倒立的树,叶子在下端,根在最上面
一层一层连接的是交内部节点,内部节点主要是一些条件判断表达式,叶子叫叶节点,叶节点其实就是最终的预测结果,那么当输入x进去,一层一层的进行选择,就到最后的叶子节点,就完成整个流程,叶子节点的值就是最终的值。
决策树经常用来做分类任务,下面是基本的决策树的结构
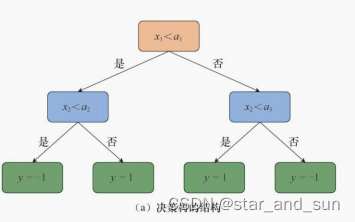
决策树的构造
在构造决策树的时候需要尽可能的减少模型的复杂度,可见决策树的层数和节点数不要过多才最好。
X,Y的取值范围是1,。。。,n 则信息熵的公式
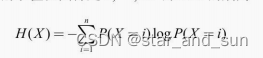
交叉熵
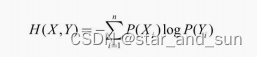
条件熵
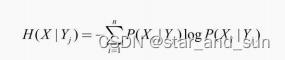
信息增益
**I=H(X)-H(X|Y)**
信息增益率
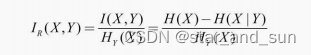
其中
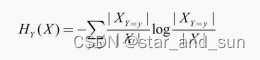
采用信息增益率可以减少模型整体的复杂度。
ID3和C4.5
ID3算法是基于信息增益来做的,C4.5是结合信息增益率来做的,只能解决分类问题。

CART算法
ID3算法,C4.5只能解决分类问题。在回归问题中,采用CART算法,其采用了误差的平方作为标准

此外CART算法可以解决分类问题

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd# 读取数据
data = pd.read_csv('titanic/train.csv')
# 查看数据集信息和前5行具体内容,其中NaN代表数据缺失
print(data.info())
print(data[:5])# 删去编号、姓名、船票编号3列
data.drop(columns=['PassengerId', 'Name', 'Ticket'], inplace=True)
#%%
feat_ranges = {}
cont_feat = ['Age', 'Fare'] # 连续特征
bins = 10 # 分类点数for feat in cont_feat:# 数据集中存在缺省值nan,需要用np.nanmin和np.nanmaxmin_val = np.nanmin(data[feat]) max_val = np.nanmax(data[feat])feat_ranges[feat] = np.linspace(min_val, max_val, bins).tolist()print(feat, ':') # 查看分类点for spt in feat_ranges[feat]:print(f'{spt:.4f}')
#%%
# 只有有限取值的离散特征
cat_feat = ['Sex', 'Pclass', 'SibSp', 'Parch', 'Cabin', 'Embarked']
for feat in cat_feat:data[feat] = data[feat].astype('category') # 数据格式转为分类格式print(f'{feat}:{data[feat].cat.categories}') # 查看类别data[feat] = data[feat].cat.codes.to_list() # 将类别按顺序转换为整数ranges = list(set(data[feat]))ranges.sort()feat_ranges[feat] = ranges
#%%
# 将所有缺省值替换为-1
data.fillna(-1, inplace=True)
for feat in feat_ranges.keys():feat_ranges[feat] = [-1] + feat_ranges[feat]
#%%
# 划分训练集与测试集
np.random.seed(0)
feat_names = data.columns[1:]
label_name = data.columns[0]
# 重排下标之后,按新的下标索引数据
data = data.reindex(np.random.permutation(data.index))
ratio = 0.8
split = int(ratio * len(data))
train_x = data[:split].drop(columns=['Survived']).to_numpy()
train_y = data['Survived'][:split].to_numpy()
test_x = data[split:].drop(columns=['Survived']).to_numpy()
test_y = data['Survived'][split:].to_numpy()
print('训练集大小:', len(train_x))
print('测试集大小:', len(test_x))
print('特征数:', train_x.shape[1])
#%%
class Node:def __init__(self):# 内部结点的feat表示用来分类的特征编号,其数字与数据中的顺序对应# 叶结点的feat表示该结点对应的分类结果self.feat = None# 分类值列表,表示按照其中的值向子结点分类self.split = None# 子结点列表,叶结点的child为空self.child = []
#%%
class DecisionTree:def __init__(self, X, Y, feat_ranges, lbd):self.root = Node()self.X = Xself.Y = Yself.feat_ranges = feat_ranges # 特征取值范围self.lbd = lbd # 正则化系数self.eps = 1e-8 # 防止数学错误log(0)和除以0self.T = 0 # 记录叶结点个数self.ID3(self.root, self.X, self.Y)# 工具函数,计算 a * log adef aloga(self, a):return a * np.log2(a + self.eps)# 计算某个子数据集的熵def entropy(self, Y):cnt = np.unique(Y, return_counts=True)[1] # 统计每个类别出现的次数N = len(Y)ent = -np.sum([self.aloga(Ni / N) for Ni in cnt])return ent# 计算用feat <= val划分数据集的信息增益def info_gain(self, X, Y, feat, val):# 划分前的熵N = len(Y)if N == 0:return 0HX = self.entropy(Y)HXY = 0 # H(X|Y)# 分别计算H(X|X_F<=val)和H(X|X_F>val)Y_l = Y[X[:, feat] <= val]HXY += len(Y_l) / len(Y) * self.entropy(Y_l)Y_r = Y[X[:, feat] > val]HXY += len(Y_r) / len(Y) * self.entropy(Y_r)return HX - HXY# 计算特征feat <= val本身的复杂度H_Y(X)def entropy_YX(self, X, Y, feat, val):HYX = 0N = len(Y)if N == 0:return 0Y_l = Y[X[:, feat] <= val]HYX += -self.aloga(len(Y_l) / N)Y_r = Y[X[:, feat] > val]HYX += -self.aloga(len(Y_r) / N)return HYX# 计算用feat <= val划分数据集的信息增益率def info_gain_ratio(self, X, Y, feat, val):IG = self.info_gain(X, Y, feat, val)HYX = self.entropy_YX(X, Y, feat, val)return IG / HYX# 用ID3算法递归分裂结点,构造决策树def ID3(self, node, X, Y):# 判断是否已经分类完成if len(np.unique(Y)) == 1:node.feat = Y[0]self.T += 1return# 寻找最优分类特征和分类点best_IGR = 0best_feat = Nonebest_val = Nonefor feat in range(len(feat_names)):for val in self.feat_ranges[feat_names[feat]]:IGR = self.info_gain_ratio(X, Y, feat, val)if IGR > best_IGR:best_IGR = IGRbest_feat = featbest_val = val# 计算用best_feat <= best_val分类带来的代价函数变化# 由于分裂叶结点只涉及该局部,我们只需要计算分裂前后该结点的代价函数# 当前代价cur_cost = len(Y) * self.entropy(Y) + self.lbd# 分裂后的代价,按best_feat的取值分类统计# 如果best_feat为None,说明最优的信息增益率为0,# 再分类也无法增加信息了,因此将new_cost设置为无穷大if best_feat is None:new_cost = np.infelse:new_cost = 0X_feat = X[:, best_feat]# 获取划分后的两部分,计算新的熵new_Y_l = Y[X_feat <= best_val]new_cost += len(new_Y_l) * self.entropy(new_Y_l)new_Y_r = Y[X_feat > best_val]new_cost += len(new_Y_r) * self.entropy(new_Y_r)# 分裂后会有两个叶结点new_cost += 2 * self.lbdif new_cost <= cur_cost:# 如果分裂后代价更小,那么执行分裂node.feat = best_featnode.split = best_vall_child = Node()l_X = X[X_feat <= best_val]l_Y = Y[X_feat <= best_val]self.ID3(l_child, l_X, l_Y)r_child = Node()r_X = X[X_feat > best_val]r_Y = Y[X_feat > best_val]self.ID3(r_child, r_X, r_Y)node.child = [l_child, r_child]else:# 否则将当前结点上最多的类别作为该结点的类别vals, cnt = np.unique(Y, return_counts=True)node.feat = vals[np.argmax(cnt)]self.T += 1# 预测新样本的分类def predict(self, x):node = self.root# 从根结点开始向下寻找,到叶结点结束while node.split is not None:# 判断x应该处于哪个子结点if x[node.feat] <= node.split:node = node.child[0]else:node = node.child[1]# 到达叶结点,返回类别return node.feat# 计算在样本X,标签Y上的准确率def accuracy(self, X, Y):correct = 0for x, y in zip(X, Y):pred = self.predict(x)if pred == y:correct += 1return correct / len(Y)
#%%
DT = DecisionTree(train_x, train_y, feat_ranges, lbd=1.0)
print('叶结点数量:', DT.T)# 计算在训练集和测试集上的准确率
print('训练集准确率:', DT.accuracy(train_x, train_y))
print('测试集准确率:', DT.accuracy(test_x, test_y))
#%%
from sklearn import tree# criterion表示分类依据,max_depth表示树的最大深度
# entropy生成的是C4.5分类树
c45 = tree.DecisionTreeClassifier(criterion='entropy', max_depth=6)
c45.fit(train_x, train_y)
# gini生成的是CART分类树
cart = tree.DecisionTreeClassifier(criterion='gini', max_depth=6)
cart.fit(train_x, train_y)c45_train_pred = c45.predict(train_x)
c45_test_pred = c45.predict(test_x)
cart_train_pred = cart.predict(train_x)
cart_test_pred = cart.predict(test_x)
print(f'训练集准确率:C4.5:{np.mean(c45_train_pred == train_y)},' \f'CART:{np.mean(cart_train_pred == train_y)}')
print(f'测试集准确率:C4.5:{np.mean(c45_test_pred == test_y)},' \f'CART:{np.mean(cart_test_pred == test_y)}')
#%%
!pip install pydotplusfrom six import StringIO
import pydotplusdot_data = StringIO()
tree.export_graphviz( # 导出sklearn的决策树的可视化数据c45,out_file=dot_data,feature_names=feat_names,class_names=['non-survival', 'survival'],filled=True, rounded=True,impurity=False
)
# 用pydotplus生成图像
graph = pydotplus.graph_from_dot_data(dot_data.getvalue().replace('\n', ''))
graph.write_png('tree.png')
