当前位置：首页 > news >正文

【一百零八】【算法分析与设计】P1908 逆序对,P1637 三元上升子序列,树状数组区间和应用

news 2025/7/13 1:26:55

P1908 逆序对

逆序对

题目描述

猫猫 TOM 和小老鼠 JERRY 最近又较量上了，但是毕竟都是成年人，他们已经不喜欢再玩那种你追我赶的游戏，现在他们喜欢玩统计。

最近，TOM 老猫查阅到一个人类称之为“逆序对”的东西，这东西是这样定义的：对于给定的一段正整数序列，逆序对就是序列中 $a_i>a_j$
且 $i < j$ 的有序对。知道这概念后，他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。注意序列中可能有重复数字。

Update:数据已加强。

输入格式

第一行，一个数 $n$ ，表示序列中有 $n$ 个数。

第二行 $n$ 个数，表示给定的序列。序列中每个数字不超过 $10^9$ 。

输出格式

输出序列中逆序对的数目。

样例 #1

样例输入 #1

6 5 4 2 6 3 1

样例输出 #1

11

提示

对于 $25\%$ 的数据， $\leq 2500$

对于 $50\%$ 的数据， $\leq 4 \times 10^4$ 。

对于所有数据， $\leq 5 \times 10^5$

请使用较快的输入输出

应该不会 $O(n^2)$ 过 50 万吧 by chen_zhe

求解逆序对的个数,按照每一个下标对应元素,以这个元素为二元组前者所拥有的逆序对的个数.
二元组意思是下标{i,j}组合,并且满足i<j.这样作为一个二元组.arr数组中有1~n下标的元素,遍历所有位置的元素,考虑i位置元素作为二元组中,下标较小的一个,看这样的元素构成的逆序对有多少个.

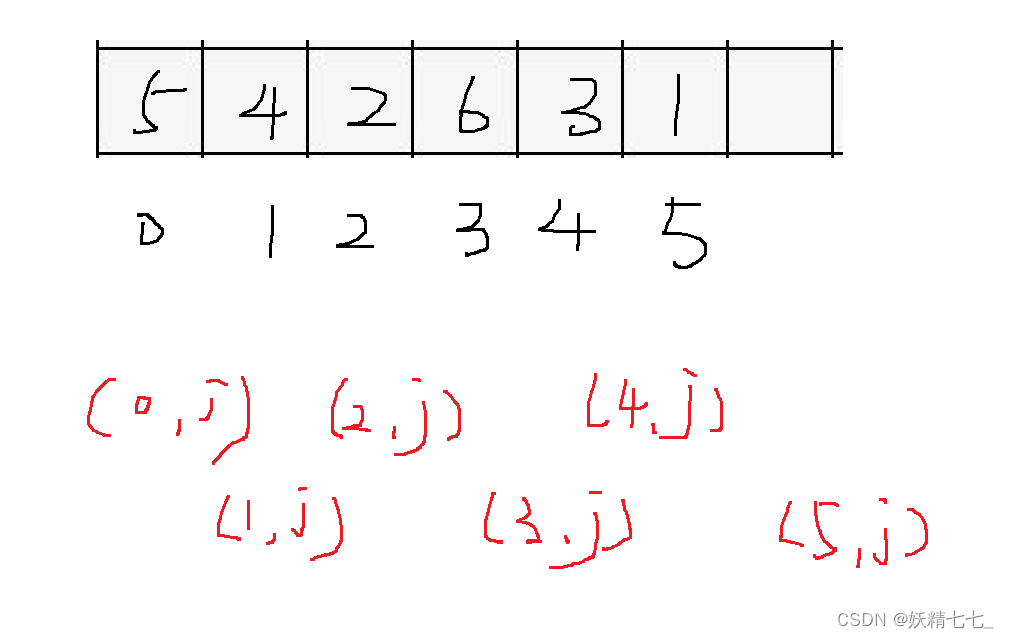
在这里插入图片描述
分别考虑0下标作为二元组较小下标,这样的所有二元组中的逆序对的个数.再考虑1下标作为二元组较小下标,这样的所有二元组中的逆序对的个数,依次类推,
很容易发现这样的详略可以不重不漏遍历所有的情况.

考虑i位置元素作为二元组较小下标,此时要求逆序对的个数,我们需要直到下标i+1~n区间中所有元素值小于i位置元素值的个数,个数就是逆序对的个数.
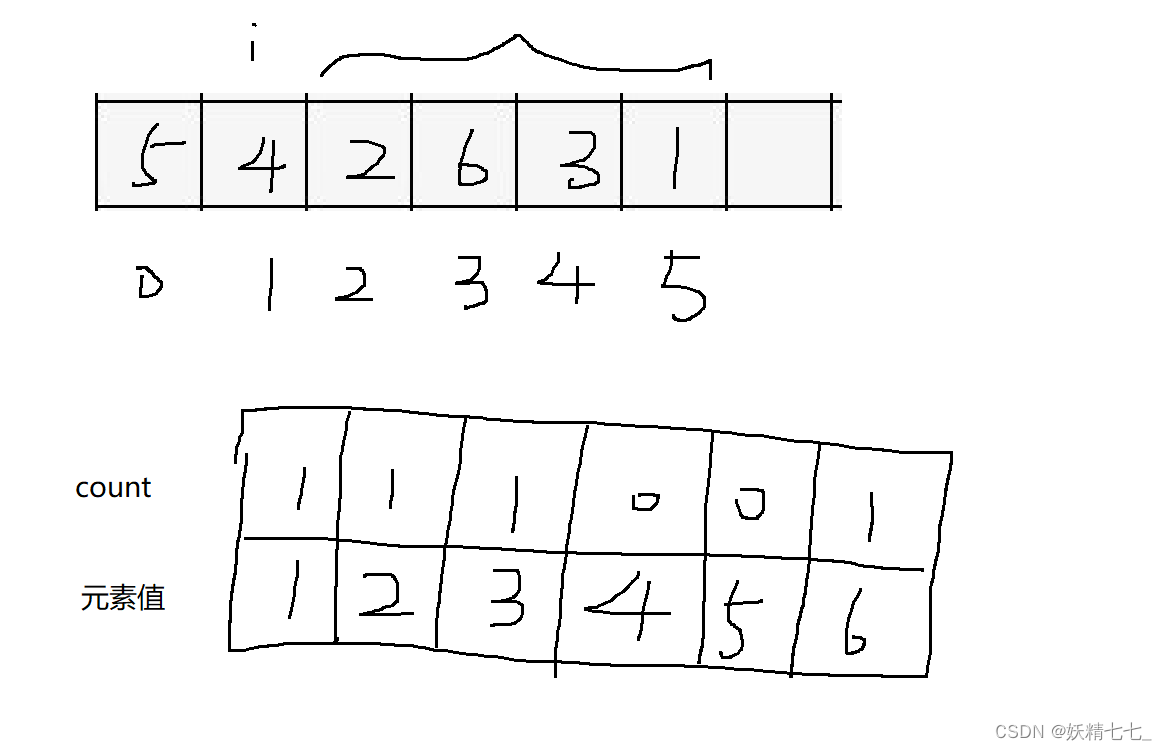
在这里插入图片描述
构建元素值映射个数的结构,只需要遍历<=i-1的前缀和即可.
很容易发现元素值映射个数结构,元素值可能是负数,并且不需要12345678连续的不少的元素值映射个数.
如果arr数组分别是145563,我们发现2元素值一直都没出现,所以2映射数量是可以不需要的.
因此需要做离散化操作.

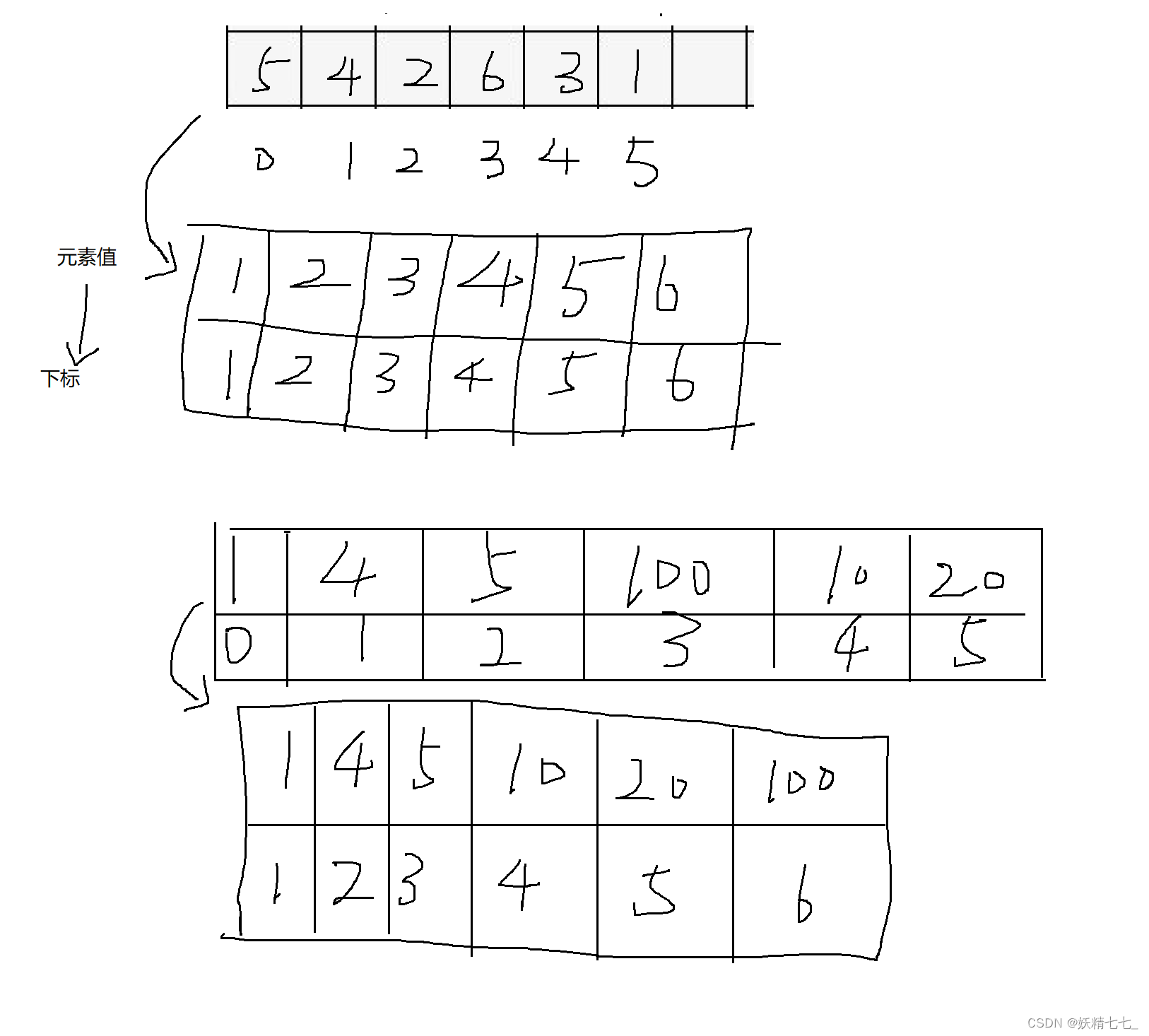
在这里插入图片描述

离散化操作,元素值按照从小到大排序并且去重,元素值映射下标,下标从1开始,依次对应.
只需要利用map结构,将所有的元素值加入map中,然后遍历map依次赋值second为1,2,3,…以此类推.
这样我们只需要构建index映射数量的结构,index一定是正数,并且是连续的.

从后往前遍历i位置元素,查询逆序对个数,arr[i]映射index,1~index-1的前缀和,得到的就是逆序对的个数.
更新index位置的个数.以此类推.

动态维护单点更新和区间和操作,利用树状数组.

#include<bits/stdc++.h>
using namespace std;#define int long long
#define endl '\n'int n; // 定义一个全局变量 n，表示序列中的数目
vector<int> arr; // 定义一个全局向量 arr，用来存储输入的序列
int ret; // 定义一个全局变量 ret，用来存储逆序对的数量
map<int, int> arr_index; // 定义一个全局 map，用来存储序列中每个数字的索引// 树状数组类定义
class Tree {
public:vector<int> tree; // 定义一个向量 tree，用来存储树状数组// 计算 lowbitint lowbit(int i) {return i & -i; // 返回 i 和 -i 的按位与，获取最低位的 1}// 在树状数组中增加值void add(int i, int k) {while (i <= n) { // 从索引 i 开始，向上更新树状数组tree[i] += k; // 增加 ki += lowbit(i); // 移动到下一个需要更新的位置}}// 计算前缀和int sum(int i) {int ret = 0; // 初始化结果为 0while (i > 0) { // 从索引 i 开始，向下计算前缀和ret += tree[i]; // 加上当前索引的值i -= lowbit(i); // 移动到下一个需要计算的位置}return ret; // 返回前缀和}// 计算区间和int range(int l, int r) {return sum(r) - sum(l - 1); // 返回区间 [l, r] 的和}// 默认构造函数Tree() {}// 使用给定数组构造树状数组Tree(vector<int> arr) {tree.assign(arr.size(), 0); // 初始化树状数组for (int i = 1; i <= arr.size(); i++) {add(i, arr[i]); // 将数组中的值添加到树状数组中}}
};Tree t1; // 定义一个全局的树状数组对象// 主解题函数
void solve() {ret = 0; // 初始化逆序对数量为 0t1.tree.assign(n + 5, 0); // 初始化树状数组的大小int index = 1; // 初始化索引为 1for (auto& xx : arr_index) {xx.second = index++; // 给每个数字分配一个唯一的索引}for (int i = n; i >= 1; i--) {int index = arr_index[arr[i]]; // 获取当前数字的索引ret += t1.sum(index - 1); // 计算比当前数字小的数字的数量t1.add(index, 1); // 在树状数组中增加当前数字}cout << ret << endl; // 输出逆序对数量
}signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 快速输入输出cin >> n; // 读取序列的长度arr.assign(n + 5, 0); // 初始化序列数组for (int i = 1; i <= n; i++) {cin >> arr[i]; // 读取序列中的每个数字arr_index[arr[i]]; // 在 map 中记录每个数字}solve(); // 调用解题函数
}

P1637 三元上升子序列

三元上升子序列

题目描述

Erwin 最近对一种叫 thair 的东西巨感兴趣。。。

在含有 $n$ 个整数的序列 $a_1,a_2,\ldots,a_n$ 中，三个数被称作thair当且仅当 $i < j < k$ 且
$a_i<a_j<a_k$ 。

求一个序列中 thair 的个数。

输入格式

开始一行一个正整数 $n$ ,

以后一行 $n$ 个整数 $a_1,a_2,\ldots,a_n$ 。

输出格式

一行一个整数表示 thair 的个数。

样例 #1

样例输入 #1

4 2 1 3 4

样例输出 #1

2

样例 #2

样例输入 #2

5 1 2 2 3 4

样例输出 #2

7

提示

样例2 解释

$7$ 个 thair 分别是：

1 2 3
1 2 4
1 2 3
1 2 4
1 3 4
2 3 4
2 3 4

数据规模与约定

对于 $30\%$ 的数据保证 $n\le100$ ；
对于 $60\%$ 的数据保证 $n\le2000$ ；
对于 $100\%$ 的数据保证 $\leq n\le3\times10^4$ ， $1\le a_i\leq 10^5$ 。

递增三元组,遍历每一个位置元素i,i作为三元组最右侧的k下标,最大的下标,此时拥有的递增三元组的个数.
等价于求1~i-1位置小于我当前位置元素值的递增二元组的个数.
如果一个数组存储1~i-1映射二元组个数,只需要i求前缀和.

维护二元组数组,遍历每一个位置元素i,作为二元组较大的下标,此时拥有的二元组的个数是1~i-1中有多少个比我小的元素个数.
利用上一道题的思路可以利用数组数组求1~i-1中有多少比我小的元素个数.

#include<bits/stdc++.h>
using namespace std;#define int long long // 定义 int 为 long long 类型，方便处理大数
#define endl '\n' // 定义换行符为 endl，方便输出int n; // 定义全局变量 n，表示序列中的数目
vector<int> arr; // 定义全局向量 arr，用于存储输入的序列
int ret; // 定义全局变量 ret，用于存储三元上升子序列的数量
map<int, int> arr_index; // 定义全局 map，用于存储序列中每个数字的索引// 树状数组类定义
class Tree {
public:vector<int> tree; // 定义一个向量 tree，用于存储树状数组// 计算 lowbitint lowbit(int i) {return i & -i; // 返回 i 和 -i 的按位与，获取最低位的 1}// 在树状数组中增加值void add(int i, int k) {while (i <= n) { // 从索引 i 开始，向上更新树状数组tree[i] += k; // 增加 ki += lowbit(i); // 移动到下一个需要更新的位置}}// 计算前缀和int sum(int i) {int ret = 0; // 初始化结果为 0while (i > 0) { // 从索引 i 开始，向下计算前缀和ret += tree[i]; // 加上当前索引的值i -= lowbit(i); // 移动到下一个需要计算的位置}return ret; // 返回前缀和}// 计算区间和int range(int l, int r) {return sum(r) - sum(l - 1); // 返回区间 [l, r] 的和}// 默认构造函数Tree() {}// 使用给定数组构造树状数组Tree(vector<int> arr) {tree.assign(arr.size(), 0); // 初始化树状数组for (int i = 1; i <= arr.size(); i++) {add(i, arr[i]); // 将数组中的值添加到树状数组中}}
};Tree t1, t2; // 定义两个全局的树状数组对象// 主解题函数
void solve() {t1.tree.assign(n + 5, 0); // 初始化第一个树状数组的大小t2.tree.assign(n + 5, 0); // 初始化第二个树状数组的大小int index = 1; // 初始化索引为 1for (auto& xx : arr_index) {xx.second = index++; // 给每个数字分配一个唯一的索引}ret = 0; // 初始化三元上升子序列的数量为 0for (int i = 1; i <= n; i++) {int index = arr_index[arr[i]]; // 获取当前数字的索引t1.add(index, 1); // 在第一个树状数组中增加当前数字t2.add(index, t1.sum(index - 1)); // 在第二个树状数组中增加当前数字左侧比它小的数字的数量ret += t2.sum(index - 1); // 累加比当前数字小的数字的数量，得到三元上升子序列的数量}cout << ret << endl; // 输出三元上升子序列的数量
}signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 快速输入输出cin >> n; // 读取序列的长度arr.assign(n + 5, 0); // 初始化序列数组for (int i = 1; i <= n; i++) {cin >> arr[i]; // 读取序列中的每个数字arr_index[arr[i]]; // 在 map 中记录每个数字}solve(); // 调用解题函数
}