当前位置： 首页 > news >正文

LeetCode---二叉树

news 2025/7/29 12:34:34

144/94/145. 二叉树的前、中、后序的递归遍历

以中序遍历为例，其余类似：

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

代码示例： 

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* cur,vector<int>& vec){if(cur == NULL) return;traversal(cur->left,vec);//左vec.push_back(cur->val);//中traversal(cur->right,vec);//右}vector<int> inorderTraversal(TreeNode* root) {vector<int> result;traversal(root,result);return result;}
};

总结：不同的遍历方式只需将前中后三行代码交换顺序即可

递归三要素： 

  1. 确定递归函数的参数和返回值： 确定哪些参数是递归的过程中需要处理的，那么就在递归函数里加上这个参数， 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。

  2. 确定终止条件： 写完了递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。

  3. 确定单层递归的逻辑： 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。

144/94/145. 二叉树的前、中、后序的非递归遍历(迭代)

1. 前序遍历和后续遍历：遍历节点和处理节点相同，可共用一套规则

2. 中序遍历：遍历节点和处理节点不相同

前序遍历：

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top();                       // 中st.pop();result.push_back(node->val);if (node->right) st.push(node->right);           // 右（空节点不入栈）if (node->left) st.push(node->left);             // 左（空节点不入栈）}return result;}
};

后序遍历：

class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top();st.pop();result.push_back(node->val);if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）if (node->right) st.push(node->right); // 空节点不入栈}reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了return result;}
};
  1. 处理：将元素放进result数组中
  2. 访问：遍历节点

中序遍历： 

class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;TreeNode* cur = root;while (cur != NULL || !st.empty()) {if (cur != NULL) { // 指针来访问节点，访问到最底层st.push(cur); // 将访问的节点放进栈cur = cur->left;                // 左} else {cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）st.pop();result.push_back(cur->val);     // 中cur = cur->right;               // 右}}return result;}
};

102. 二叉树的层序遍历 

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

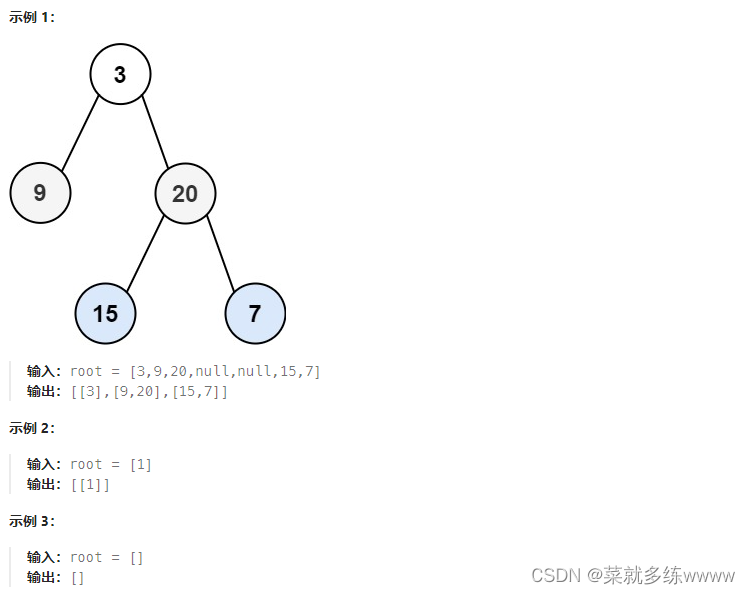
代码示例：

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> que;vector<vector<int>> result;if(root != NULL) que.push(root);while(!que.empty()){int size = que.size();vector<int> vec;while(size--){TreeNode* node = que.front();que.pop();vec.push_back(node->val);if(node->left)  que.push(node->left);if(node->right) que.push(node->right);}result.push_back(vec);}return result;}
};

107. 二叉树的层序遍历II  

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

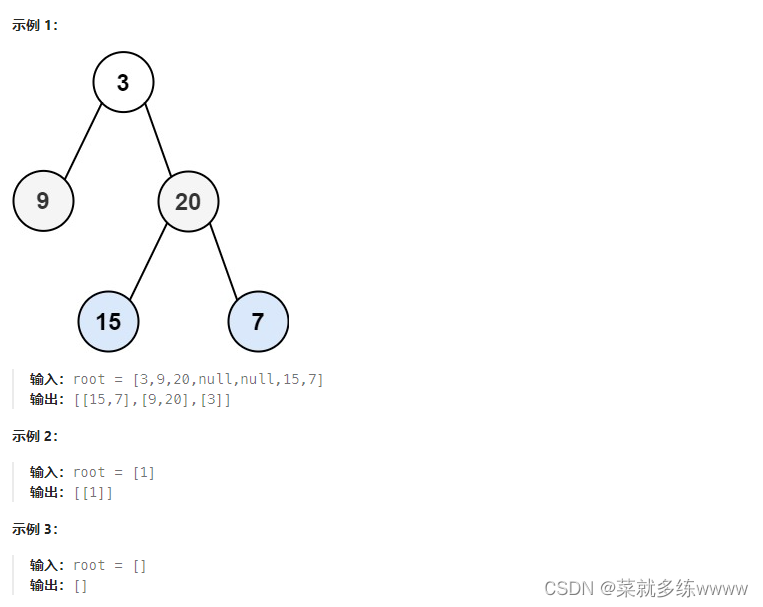
代码示例：

class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {queue<TreeNode*> que;vector<vector<int>> result;if(root != NULL) que.push(root);while(!que.empty()){int size = que.size();vector<int> vec;while(size--){TreeNode* node = que.front();que.pop();vec.push_back(node->val);if(node->left)  que.push(node->left);if(node->right) que.push(node->right);} result.push_back(vec);}reverse(result.begin(),result.end());return result;}
};

注意： 

以下写法是错的，因为reverse 函数不返回任何值（返回类型是 void），它只是对输入范围内的元素进行原地修改。

return reverse(result.begin(),result.end());

199. 二叉树的右视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

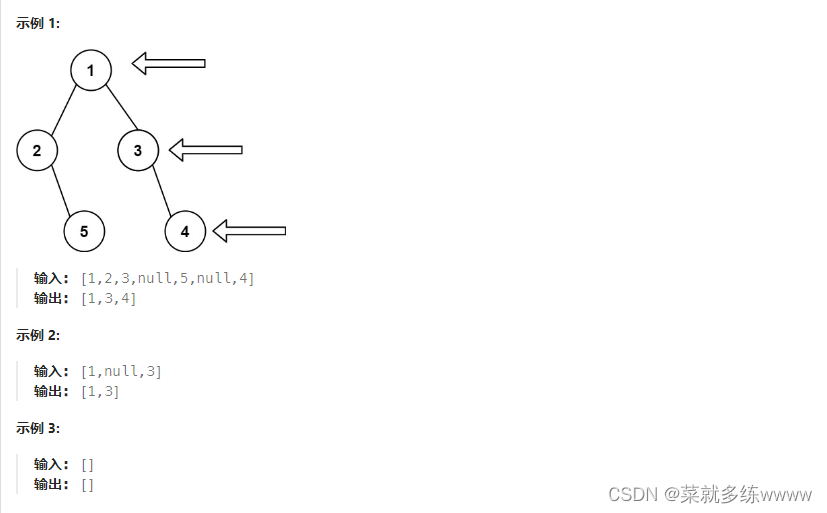
代码示例： 

class Solution {
public:vector<int> rightSideView(TreeNode* root) {queue<TreeNode*> que;vector<int> result;if(root != NULL) que.push(root);while(!que.empty()){int size = que.size();for(int i = 0;i<size;i++){TreeNode* node = que.front();que.pop();if(i == (size - 1)) result.push_back(node->val);if(node->left) que.push(node->left);if(node->right) que.push(node->right);}}   return result;}
};

226. 翻转二叉树 

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

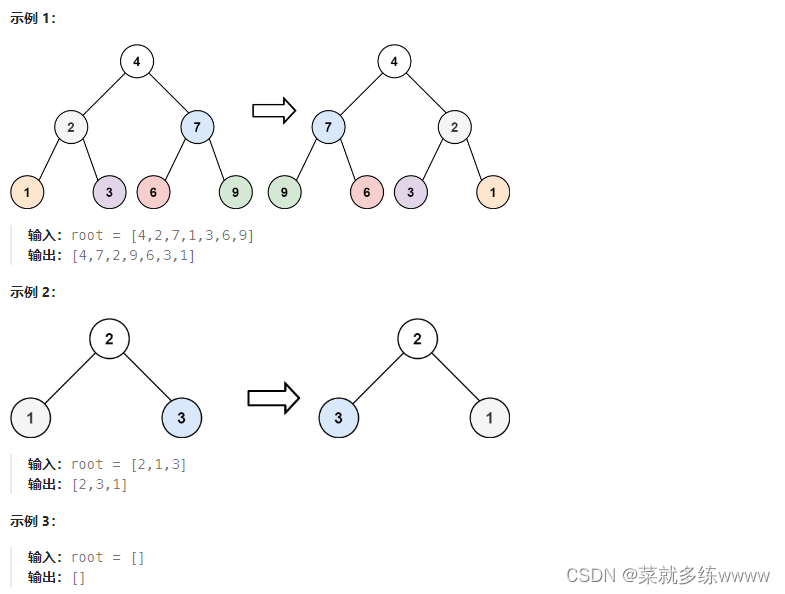
代码示例： 

class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root;swap(root->left, root->right);  // 中invertTree(root->left);         // 左invertTree(root->right);        // 右return root;}
};

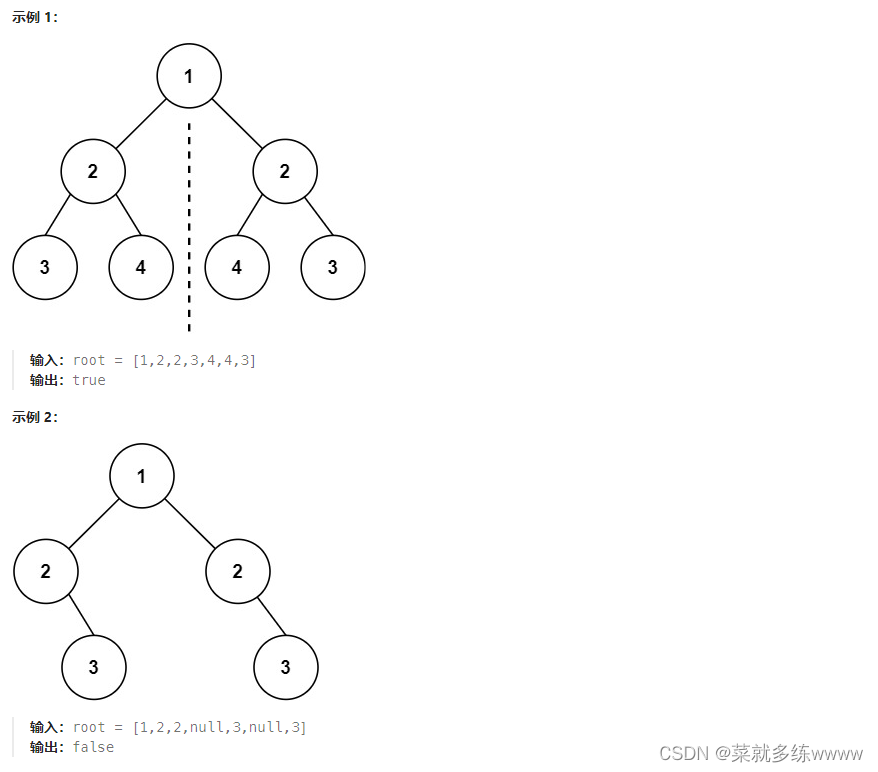
101. 对称二叉树 

给你一个二叉树的根节点 root ， 检查它是否轴对称。

代码示例： 

class Solution {
public:bool compare(TreeNode* left, TreeNode* right) {// 首先排除空节点的情况if (left == NULL && right != NULL) return false;else if (left != NULL && right == NULL) return false;else if (left == NULL && right == NULL) return true;// 排除了空节点，再排除数值不相同的情况else if (left->val != right->val) return false;// 此时就是：左右节点都不为空，且数值相同的情况// 此时才做递归，做下一层的判断bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左bool isSame = outside && inside;                    // 左子树：中、 右子树：中 （逻辑处理）return isSame;}bool isSymmetric(TreeNode* root) {if (root == NULL) return true;return compare(root->left, root->right);}
};

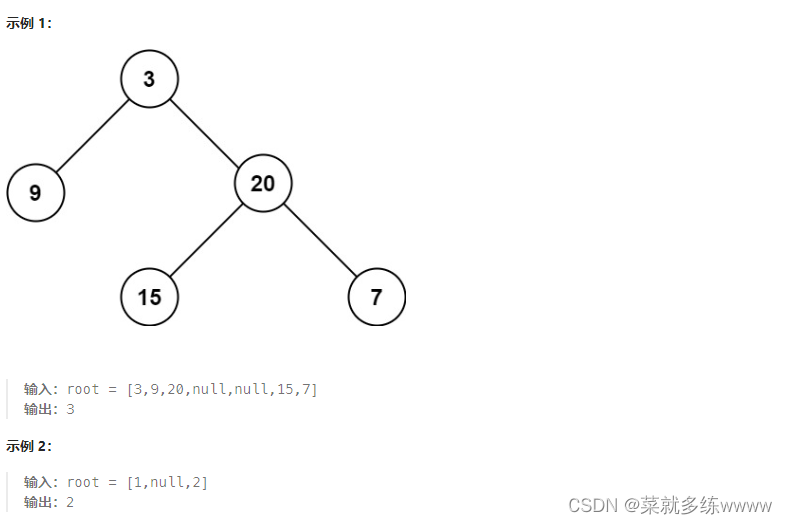
104. 二叉树的最大深度 

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

二叉树的 最大高度 是指最从远叶子节点到根节点的最长路径上的节点数。

代码示例： 

class Solution {
public:int getdepth(TreeNode* node) {if (node == NULL) return 0;int leftdepth = getdepth(node->left);       // 左int rightdepth = getdepth(node->right);     // 右int depth = 1 + max(leftdepth, rightdepth); // 中return depth;}int maxDepth(TreeNode* root) {return getdepth(root);}
};

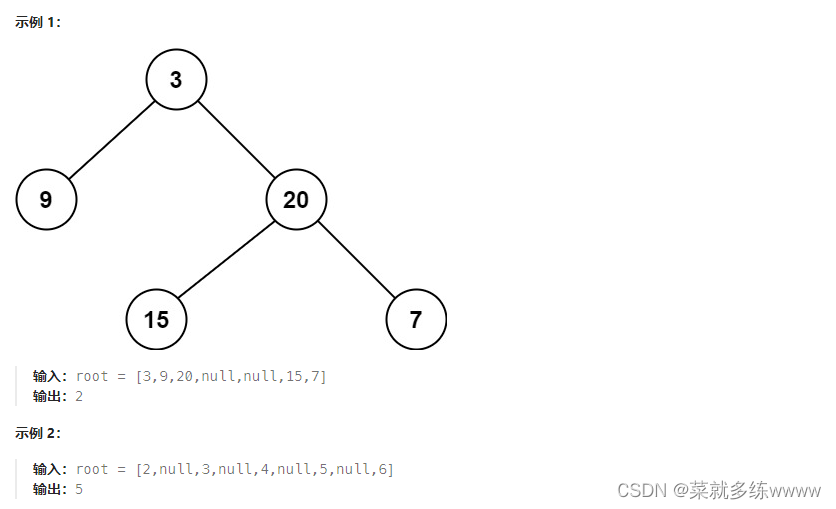
111. 二叉树的最小深度 

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

代码示例：

class Solution {
public:int getDepth(TreeNode* node) {if (node == NULL) return 0;int leftDepth = getDepth(node->left);           // 左int rightDepth = getDepth(node->right);         // 右// 中// 当一个左子树为空，右不为空，这时并不是最低点if (node->left == NULL && node->right != NULL) { return 1 + rightDepth;}   // 当一个右子树为空，左不为空，这时并不是最低点if (node->left != NULL && node->right == NULL) { return 1 + leftDepth;}int result = 1 + min(leftDepth, rightDepth);return result;}int minDepth(TreeNode* root) {return getDepth(root);}
};

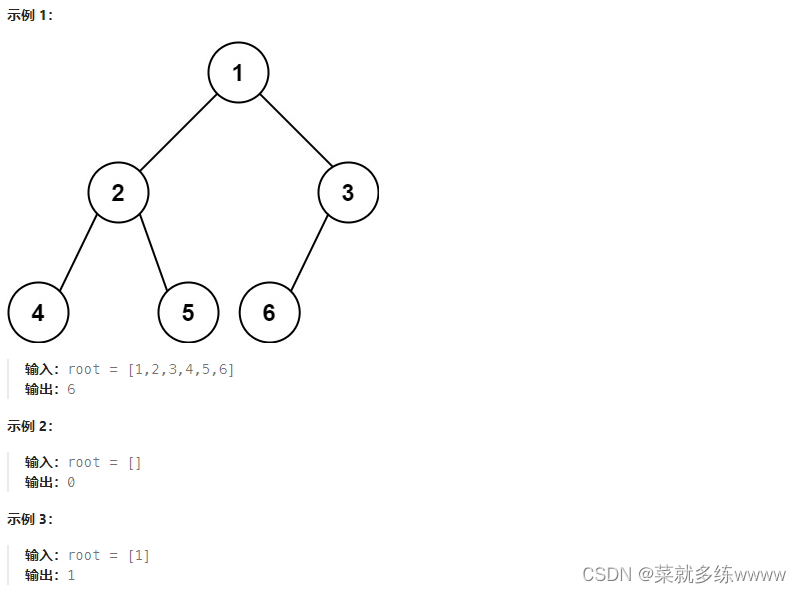
222. 完全二叉树的节点个数 

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

代码示例(普通二叉树解法)：

class Solution {
private:int getNodesNum(TreeNode* cur) {if (cur == NULL) return 0;int leftNum = getNodesNum(cur->left);      // 左int rightNum = getNodesNum(cur->right);    // 右int treeNum = leftNum + rightNum + 1;      // 中return treeNum;}
public:int countNodes(TreeNode* root) {return getNodesNum(root);}
};

完全二叉树解法：

class Solution {
public:int countNodes(TreeNode* root) {if (root == nullptr) return 0;TreeNode* left = root->left;TreeNode* right = root->right;int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便while (left) {  // 求左子树深度left = left->left;leftDepth++;}while (right) { // 求右子树深度right = right->right;rightDepth++;}if (leftDepth == rightDepth) {return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，所以leftDepth初始为0}return countNodes(root->left) + countNodes(root->right) + 1;}
};

 参考如下：

代码随想录

http://www.lryc.cn/news/366629.html

相关文章：

  • 从0开发一个Chrome插件：核心功能开发——弹出页面
  • AIGC笔记--Stable Diffusion源码剖析之UNetModel
  • Linux文件系统与日志分析
  • 【SkyWalking】使用PostgreSQL做存储K8s部署
  • 详解大模型微调数据集构建方法(持续更新)
  • 自制植物大战僵尸：HTML5与JavaScript实现的简单游戏
  • Istio_1.17.8安装
  • [数据集][目标检测]室内积水检测数据集VOC+YOLO格式761张1类别
  • 17_Vue高级监听器生命周期Vue组件组件通信
  • 【ROS使用记录】—— ros使用过程中的rosbag录制播放和ros话题信息相关的指令与操作记录
  • Laravel 富文本内容
  • Spark Python环境搭建与优化：深入剖析四个方面、五个方面、六个方面及七个关键要点
  • 【微信小程序开发】小程序中的上滑加载更多，下拉刷新是如何实现的？
  • 从 Android 恢复已删除的备份录
  • 如何使用Python中的random模块生成随机数
  • AI大数据处理与分析实战--体育问卷分析
  • C++第二十五弹---从零开始模拟STL中的list(下)
  • STM32/keil把多个c文件编译为静态库lib
  • L45---506.相对名次（java)--排序
  • 跨网段路由
  • HO-3D 数据集
  • Elasticsearch 认证模拟题 - 8
  • 【Postman接口测试】第四节.Postman接口测试项目实战（中）
  • Hadoop的Windows环境准备
  • 使用亮数据代理IP爬取PubMed文章链接和邮箱地址
  • electron调用dll时应用程序闪退
  • 单片机原理及技术（三）—— AT89S51单片机（二）（C51编程）
  • 摄影店展示服务预约小程序的作用是什么
  • 【数据分析基础】实验一 Python运算符、内置函数、序列基本用法
  • 【Redis】构建强韧的远程Redis连接与端口保障机制完美指南