[Algorithm][动态规划][两个数组的DP][正则表达式匹配][交错字符串][两个字符串的最小ASCII删除和][最长重复子数组]详细讲解
目录
- 1.正则表达式匹配
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.交错字符串
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 3.两个字符串的最小ASCII删除和
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 4.最长重复子数组
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
1.正则表达式匹配
1.题目链接
- 正则表达式匹配
2.算法原理详解
- 思路:
-
确定状态表示 ->
dp[i][j]的含义dp[i]j]:p的[0, j]区间内的子串能否匹配s的[0, i]区间内的子串
-
推导状态转移方程:根据最后一个位置的情况,分情况讨论
-
结论

-
推导过程

-
本题若直接按照如下的状态转移方程去写,时间复杂度会到 O ( N 3 ) O(N^3) O(N3)
-
所以需要想办法优化
-
-
优化:
-
方法一:数学推导
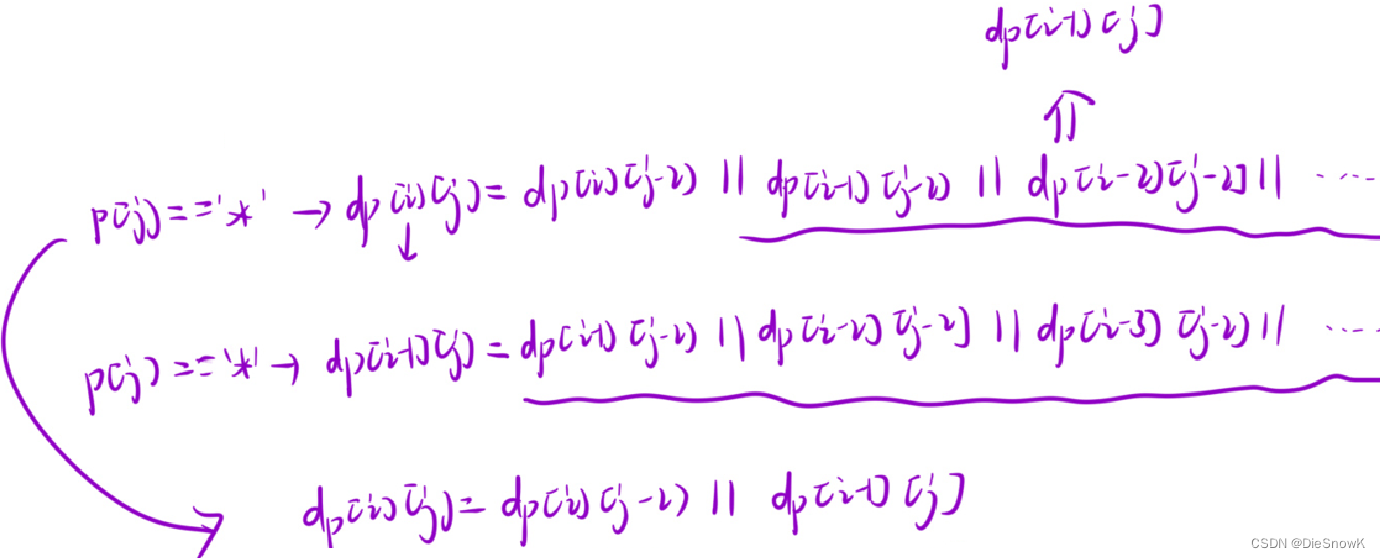
-
方法二:根据状态表示以及实际情况,优化状态转移方程 -> 抽象,难理解:(
- 实际相当于保留了
*,把状态传递给前面

- 实际相当于保留了
-
-
初始化:
- 多开一行及一列虚拟结点
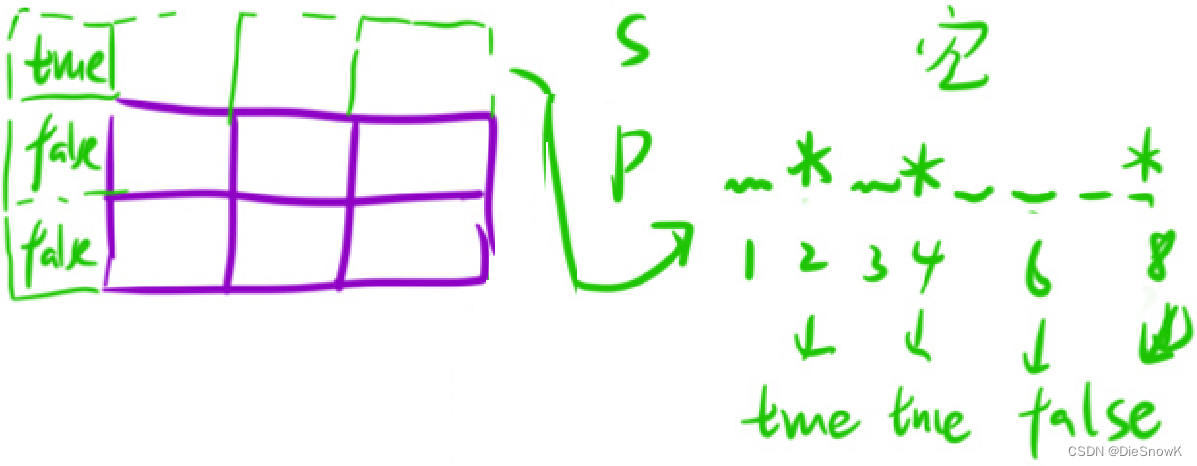
- 多开一行及一列虚拟结点
-
确定填表顺序:从上往下,从左往右
-
确定返回值:
dp[n][m]
-
3.代码实现
bool isMatch(string s, string p)
{int n = s.size(), m = p.size();s = " " + s, p = " " + p;vector<vector<bool>> dp(n + 1, vector<bool>(m + 1));// Initdp[0][0] = true;for(int i = 2; i <= m; i += 2){if(p[i] == '*'){dp[0][i] = true;}else{break;}}// DPfor(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){if(p[j] == '*'){dp[i][j] = dp[i][j - 2] || (p[j - 1] == '.' || p[j - 1] == s[i]) && dp[i - 1][j];}else{dp[i][j] = (p[j] == s[i] || p[j] == '.') && dp[i - 1][j - 1];}}}return dp[n][m];
}
2.交错字符串
1.题目链接
- 交错字符串
2.算法原理详解
-
预处理:
s1 = " " + s1, s2 = " " + s2, s3 = " " + s3- 目的:此时可以很简便的用
s1和s2的下标就计算到s3的的下标
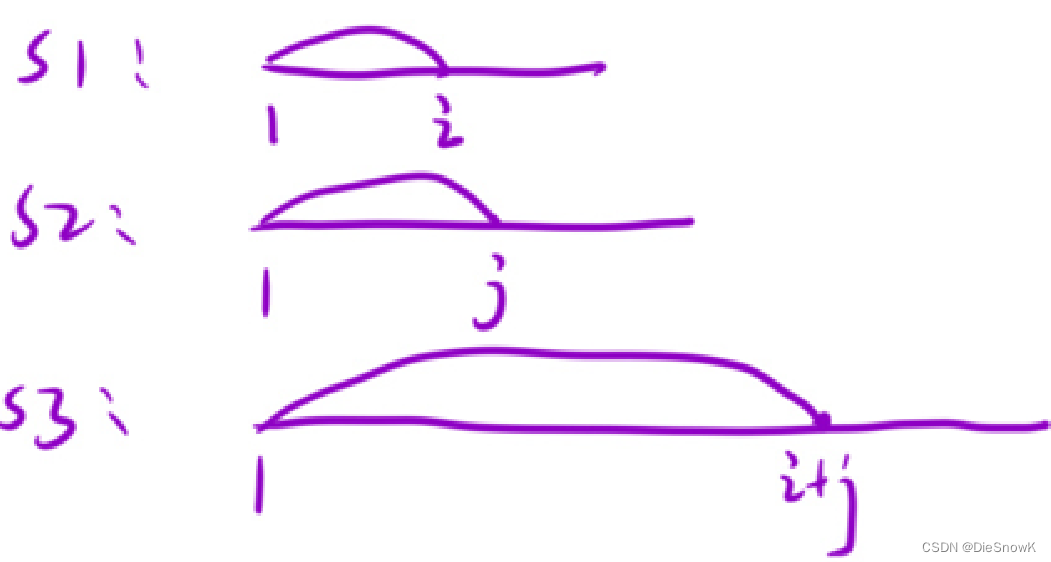
- 目的:此时可以很简便的用
-
思路:
-
确定状态表示 ->
dp[i][j]的含义dp[i]j]:s1的[1, i]区间内的字符串以及s2的[1, j]区间内的字符串,能否拼接凑成s3的[1, i + j]区间内的字符串
-
推导状态转移方程:根据最后一个位置的情况,分情况讨论
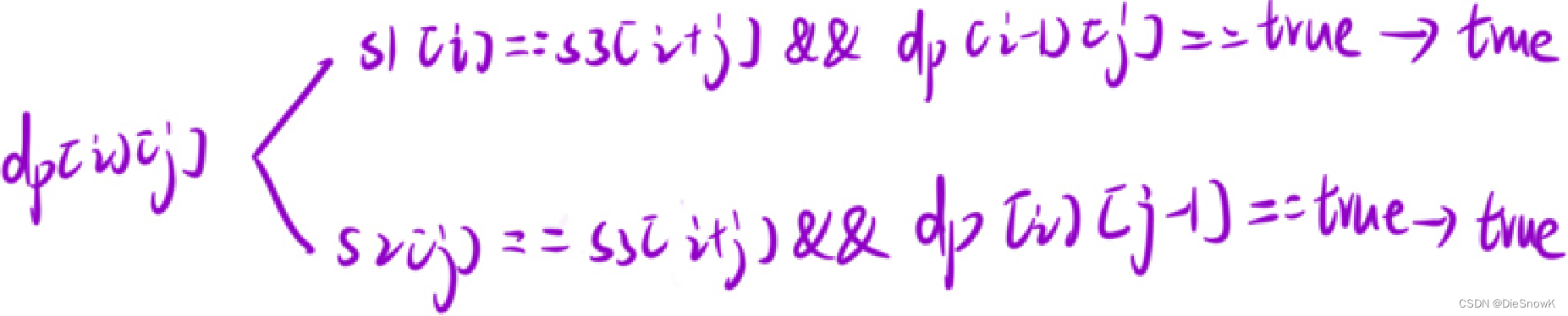
-
初始化:
- 多开一行及一列虚拟结点
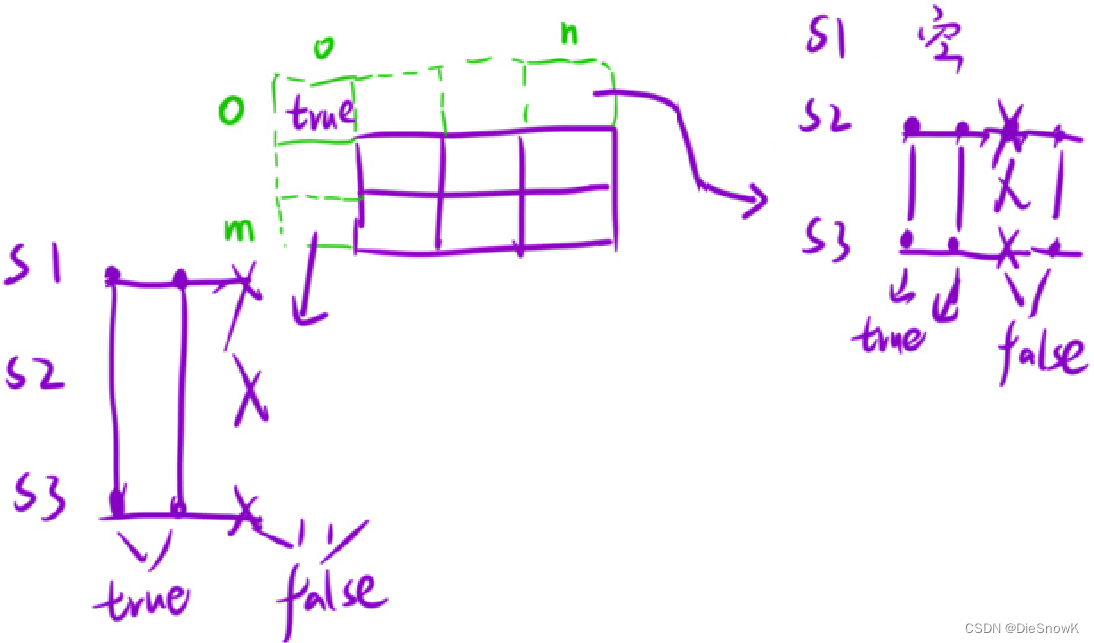
- 多开一行及一列虚拟结点
-
确定填表顺序:从上往下,从左往右
-
确定返回值:
dp[n][m]
-
3.代码实现
bool isInterleave(string s1, string s2, string s3)
{int n = s1.size(), m = s2.size();if(n + m != s3.size()) return false;s1 = " " + s1, s2 = " " + s2, s3 = " " + s3;vector<vector<bool>> dp(n + 1, vector<bool>(m + 1));// Initdp[0][0] = true;for(int i = 1; i <= m; i++) // 第一行{if(s2[i] == s3[i]){dp[0][i] = true;}else{break;}}for(int i = 1; i <= n; i++) // 第一列{if(s1[i] == s3[i]){dp[i][0] = true;}else{break;}}// DPfor(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){dp[i][j] = (s1[i] == s3[i + j] && dp[i - 1][j])|| (s2[j] == s3[i + j] && dp[i][j - 1]);}}return dp[n][m];
}
3.两个字符串的最小ASCII删除和
1.题目链接
- 两个字符串的最小ASCII删除和
2.算法原理详解
- 问题转化:删除后,公共子序列中,ASCII和最大的 —> 正难则反
- 思路:
-
确定状态表示 ->
dp[i][j]的含义dp[i]j]:s1的[0, i]区间以及s2的[0, j]区间内的所有的子序列里,公共子序列ASCII最大和
-
推导状态转移方程:根据最后一个位置的情况,分情况讨论
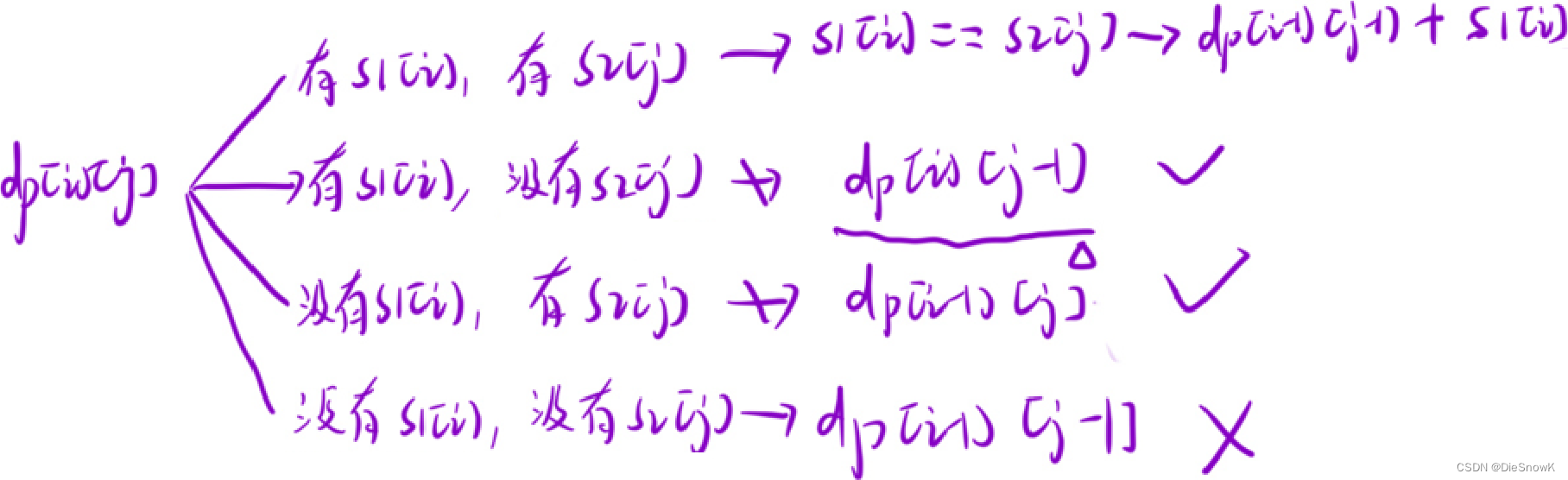
-
初始化:
vector<vector<int>> dp(n + 1, vector<int>(m + 1)) -
确定填表顺序:从上往下,从左往右
-
确定返回值:
- 统计2个字符串的ASCII和
sum sum - dp[n][m] * 2
- 统计2个字符串的ASCII和
-
3.代码实现
int minimumDeleteSum(string s1, string s2)
{int n = s1.size(), m = s2.size();vector<vector<int>> dp(n + 1, vector<int>(m + 1));for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);if(s1[i - 1] == s2[j - 1]){dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + s1[i - 1]);}}}int ret = 0;for(auto& ch : s1){ret += ch;}for(auto& ch : s2){ret += ch;}return ret - dp[n][m] * 2;
}
4.最长重复子数组
1.题目链接
- 最长重复子数组
2.算法原理详解
- 思路:
-
确定状态表示 ->
dp[i][j]的含义dp[i]:选取[0, i]一段区间内的所有子数组 ×- 因为此时无法知道最长子数组在哪儿,可能在中间,此时无法正确表示状态
dp[i][j]:nums1[i]中以i位置元素为结尾的所有的子数组以及nums2中以j位置元素为结尾的所有的子数组中,最长重复子数组的长度
-
推导状态转移方程:根据最后一个位置的情况,分情况讨论
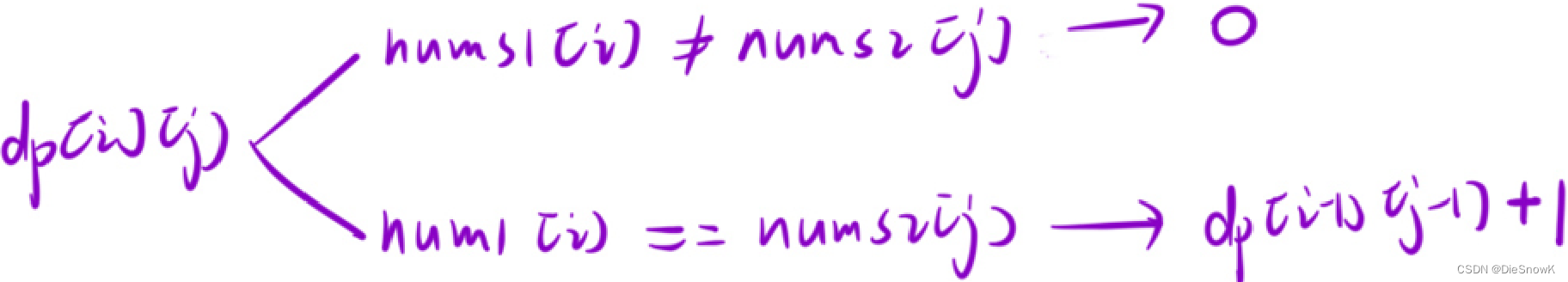
-
初始化:
vector<vector<int>> dp(n + 1, vector<int>(m + 1)) -
确定填表顺序:从上往下
-
确定返回值:
dp表里面的最大值
-
3.代码实现
int findLength(vector<int>& nums1, vector<int>& nums2)
{int n = nums1.size(), m = nums2.size();vector<vector<int>> dp(n + 1, vector<int>(m + 1));int ret = 0;for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){if(nums1[i - 1] == nums2[j - 1]){dp[i][j] = dp[i - 1][j - 1] + 1;ret = max(ret, dp[i][j]);}}}return ret;
}
