C++ 多重继承的内存布局和指针偏移
在 C++ 程序里,在有多重继承的类里面。指向派生类对象的基类指针,其实是指向了派生类对象里面,该基类对象的起始位置,该位置相对于派生类对象可能有偏移。偏移的大小,等于派生类的继承顺序表里面,排在该类前面的所有的类的数据成员(含虚表指针)所占的空间大小总和。
下面以一个简单的程序为例,揭示有多重继承关系的派生类对象的内存布局:
#include <stdio.h>
#pragma pack(4)class A {void foo() {}
};class B {
public:virtual void func() {};
private:int b;
};class C {int c;
};class D : public A, public B, public C {
public:void func() override {};
private:int d;
};int main(int argc, const char* argv[]) {D* pd = new D();A* pa = pd;B* pb = pd;C* pc = pd;printf("pd=%p, pa=%p, pb=%p, pc=%p\n""sizeof(A)=%zd\n""sizeof(B)=%zd\n""sizeof(C)=%zd\n""sizeof(D)=%zd\n",pd, pa, pb, pc,sizeof(A), sizeof(B),sizeof(C), sizeof(D));return 0;
}注意该程序用 #pragma pack 指令指示数据在内存中按 4 字节来对齐。在 x64 平台上编译执行结果:
$ g++ test.cc -std=c++11
$ ./a.out
pd=0x10c0010, pa=0x10c0010, pb=0x10c0010, pc=0x10c001c
sizeof(A)=1
sizeof(B)=12
sizeof(C)=4
sizeof(D)=20我们首先来分析这四个类的大小。
A 只有一个普通函数成员 foo,没有任何数据成员,是一个空类,其大小为 1 字节。之所以空类大小不为零,是需要标识类对象在内存中的位置,这 1 字节空间仅作占位用,不代表任何意义。
B 有一个成员变量 int b 和一个虚函数成员 func,其中 b 的大小为 4 字节。 由于存在虚函数,因此 B 类起始位置有一个虚表指针(vptr),在 64 平台上指针的大小为 8 字节。因此 B 的大小为 4 + 8 = 12 字节。
C 仅有一个成员变量 int c,因此其大小也就为 4 字节。
D 继承自A, B, C,它的大小等于 A, B, C 的所有数据成员的大小,加上其自身的数据成员和虚表指针的总的大小:4(b) + 4(c) + 4(d) + 8(vptr) = 20 字节。
注意:在 D 的继承关系链里面,只有基类 B 有虚函数,因此对于 D 对象而言,总体只有一个虚表指针,也就是(B)基类对象中的虚表指针。如果派生类的多个基类都有虚函数,则对应每个有虚函数的基类,在派生类对象里都有一个虚表指针。
因此,对于分析派生类 D 的对象,其内存布局如下:
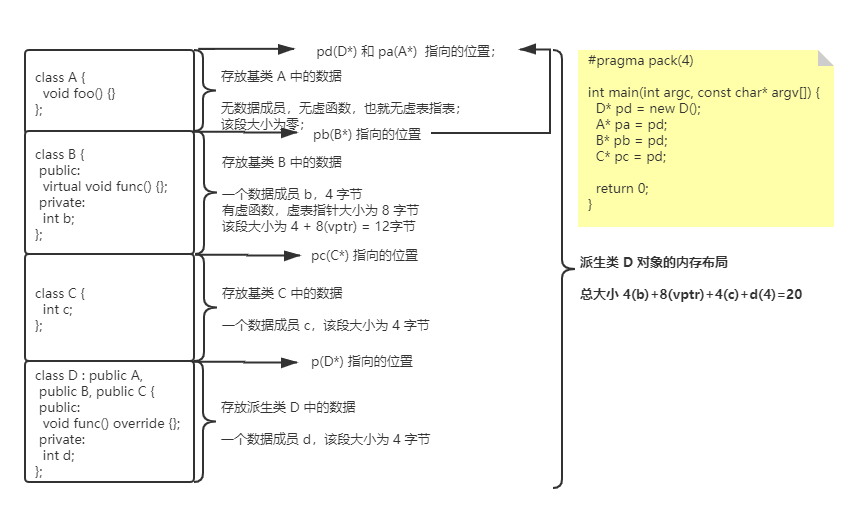
分析结果与程序运行结果一致。
