【数据结构:排序算法】堆排序(图文详解)
🎁个人主页:我们的五年
🔍系列专栏:数据结构课程学习
🎉欢迎大家点赞👍评论📝收藏⭐文章


目录
🍩1.大堆和小堆
🍩2.向上调整算法建堆和向下调整算法建堆:
🍟向上调整算法:
🍟向下调整算法:
🍟用这两种方法建堆的时间复杂度:
🍩3.堆排序:
🍩1.大堆和小堆
要想弄明白堆排序,我们先来看看大堆和小堆的概念和区别:
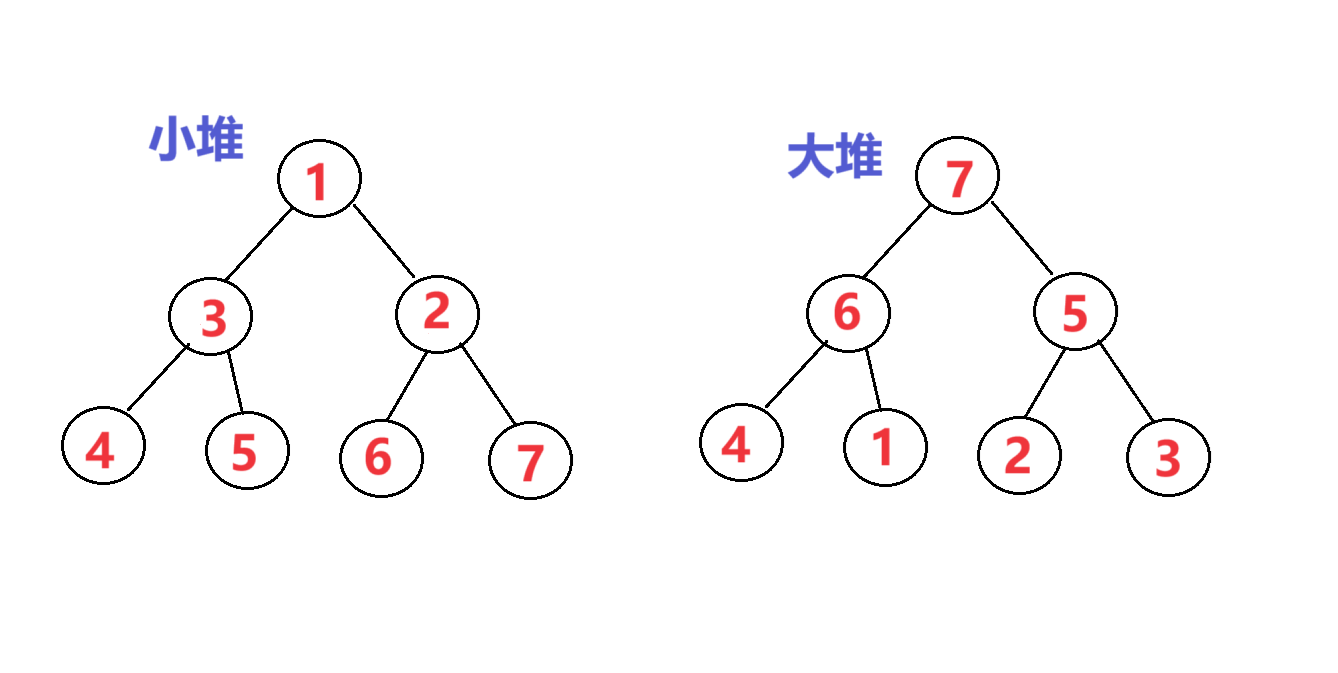
注意:堆是完全二叉树。
大堆:父节点都大于孩子节点。
小堆:父节点都小于孩子节点。
🍩2.向上调整算法建堆和向下调整算法建堆:
注:根节点我定为0
🍟向上调整算法:
向下调整算法调整该节点的前提是该节点以上的树已经是堆(大堆或者小堆),但是开始的时候,树里面的元素是随便放置的,但是可以把根元素以上看成一个堆,然后向上调整从2*0+1(第二层左边的元素)的位置开始就可以了。
以向上调整建立大堆为例:
从已经建好的堆的下一层开始向上调整,这里可以把根看成小堆,要想把整个二叉树调整为小堆形式,我们就要从根的下一层,把每个元素都进行一次向上调整。
向上调整的实现:
根该节点开始,我们把该节点与它的父节点进行比较,因为该节点以上的节点已经是大堆,此时的根是该树最大元素,所以只要和根比较谁大,如果比根大就交换位置,这样增加一个元素以后,该树还是大堆。
从上面图来看,向上调整结束的条件为该节点到达根节点,上面没有元素了。
由孩子节点的下标找到父节点的下标是:parent=(child-1)/2。
实现代码:
void AdjustUp(int* a,int child)
{//该节点开始比较int parent = (child - 1 - 1) / 2;while (child > 0) //当节点到达根节点,就没有父亲节点了,就停止{if (a[parent] < a[child]){int tmp = a[parent];a[parent] = a[child];a[child] = a[parent];child = parent;parent = (child - 1 - 1) / 2;}else{break;}}
}🍟向下调整算法:
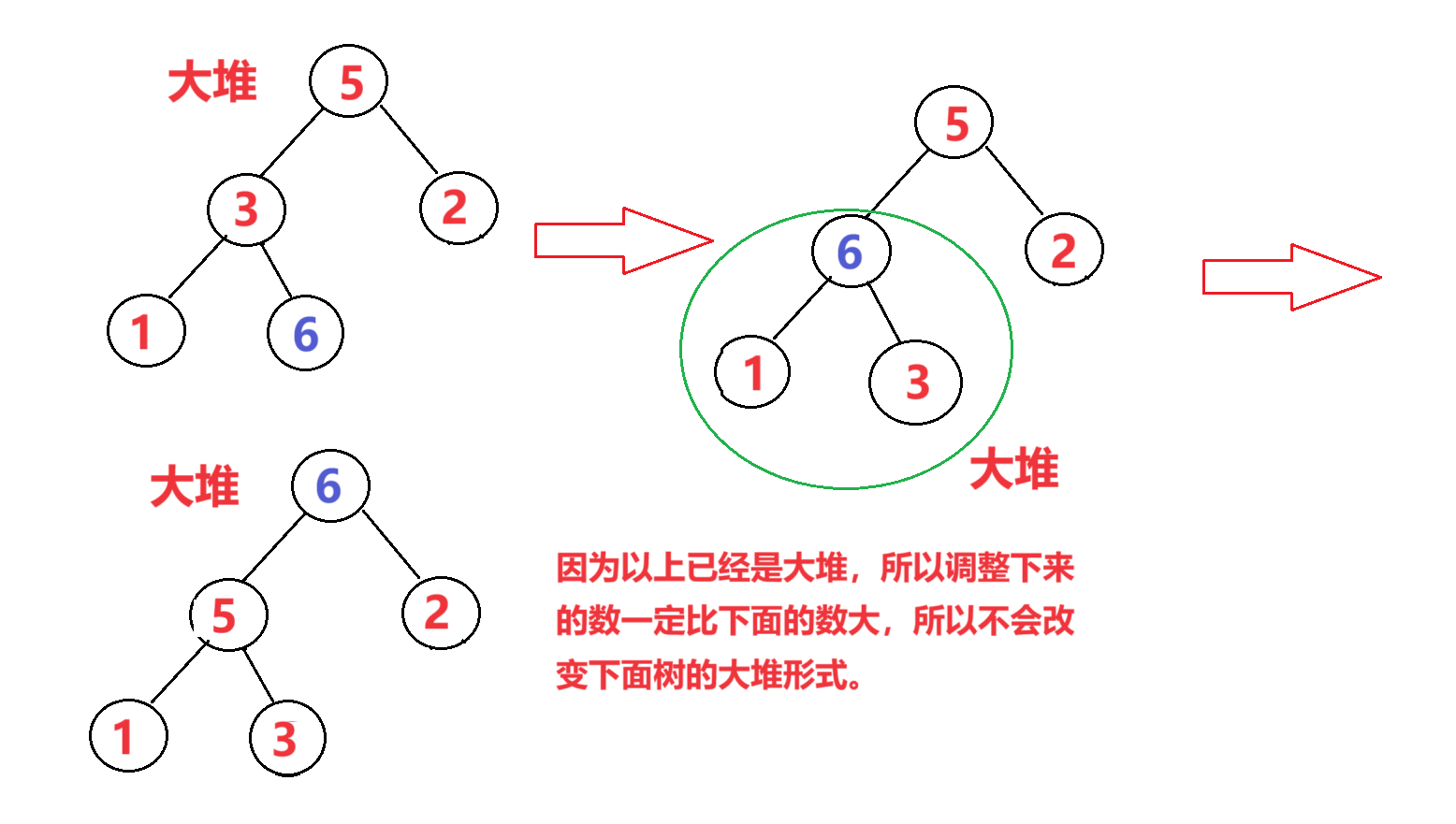
向下调整算法的要求就是左右子树已经是堆(大堆或者小堆)。结束的条件是孩子节点为NULL。
代码为:
void AdjustDown(int* a, int size, int parent)
{//假设法int child = parent * 2 + 1;while (child < size){if (child + 1 < size && a[child + 1]>a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}🍟用这两种方法建堆的时间复杂度:
假如待排序的二叉树有K层,假设为满二叉树:
如果用向上调整算法,那么进行的次数是:第1层:2^0*0 //2的0次方这这一层的节点个数,0是调整的次数,根节点向上调整的时候 ,不需要调整。
第2层:2^1*1
……
第K层:2^(k-1)*k-1
所以总的次数为:
2^0*0+2^1*1+2^2*2+……+2^(k-1)*k=(k-1)*2^k-2.
个数N=2^k-1.k=log2 (N+1)
所以O(N)=(log2 (N+1)-1)*(N+1)-2。
数量级在log N
所以O(N)=N*log N。
向下调整:
其实用向下,就可以让节点最多的调整次数最少,也就是:多*少,少*多。
而向上调整,就是:多*多,少*少。第一层的节点少,不用调整,第二层两个节点,每个调整一次,后面节点多,每个节点调整次数也多。
第k-1层:2^(k-2)*1。
第k-2层:2^(k-3)*2。
……
第2层2^1*(k-2)。
第1层2^0*(k-1)。
总的:2^0*(k-1)+2^1*(k-2)+……+2^(k-2)*1=2^k+2*k-4。
O(N)=log N。
根据上面的结论,我们知道如果要建堆,那肯定是用向下调整更好。
🍩3.堆排序:
用向下排序拍好序以后,如果我们要排升序,我们就建大堆,如果我们要排降序,我们就排小队堆。
升序:大堆。
降序:小堆。
我们以升序为例:
当得到大堆的时候,根节点是最大的,然后我们把根节点和最后的节点换一下位置,这样最大的就到最后面去了,然后我们换完以后,又用向下调整使除最后一个节点以外为大堆,这样我们取根节点,我们就的得到了第二大的,我们就把第二大的和数组的倒数第2的位置换位置,然后再让根节点向下调整建立大堆……
这样我们就能让数组升序,代码实现:
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void AdjustDown(int* a, int size, int parent)
{//假设法int child = parent * 2 + 1;while (child < size){if (child + 1 < size && a[child + 1]>a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//升序
void HeapSort(int* a, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}