数据结构 | 详解二叉树——堆与堆排序
🥝堆
大堆:父节点总是大于子节点。
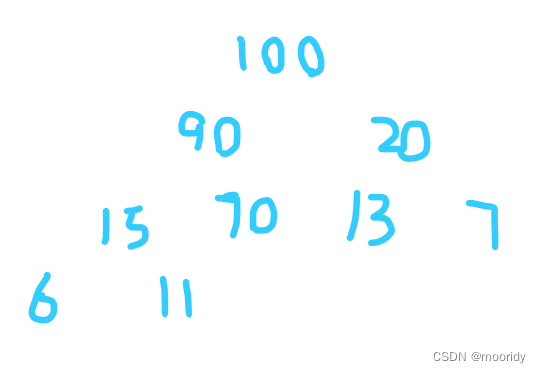
小堆:父节点总是小于子节点。
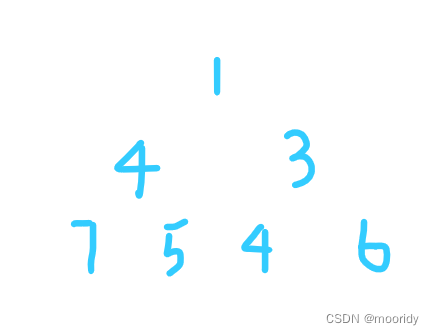
注意:1.同一个节点下的两个子节点并无要求先后顺序。
2.堆可以是无序的。
🍉堆的实现
🌴深度剖析
1.父节点和子节点之间的关系
子节点=(父节点*2)+1
或者子节点=(父节点*2)+2
父节点=(子节点-1)/2
2.堆的插入HeapPush实现
void HeapPush(Heap* php, HPDataType x) {assert(php);if (php->size == php->capacity) {int newcapacity = 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)malloc(sizeof(HPDataType) * newcapacity);if (tmp == NULL) {perror("malloc fail!");}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;AdjustUp(php->a,php->size);php->size++;
}3.堆的删除HeapPop函数的实现
函数目的:删除堆顶元素
为了避免破坏堆的整体结构,先将首尾元素进行交换,再对首元素进行向下调整,直到满足堆。最后php->size--即可删除原栈顶元素。
void HeapPop(Heap* php) {assert(php);swap(&php->a[0], &php->a[php->size - 1]);AdjustDown(php->a, php->size,0);php->size--;
}
🥳代码实现
Heap.h
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}Heap;void HeapInit(Heap* php);
// 堆的销毁
void HeapDestory(Heap* php);
// 堆的插入
void HeapPush(Heap* php, HPDataType x);
// 堆的删除
void HeapPop(Heap* php);
// 取堆顶的数据
HPDataType HeapTop(Heap* php);
// 堆的数据个数
int HeapSize(Heap* php);
// 堆的判空
int HeapEmpty(Heap* php);
Heap.c
#define _CRT_SECURE_NO_WARNINGS
#include "Heap.h"
void HeapInit(Heap* php) {assert(php);php->a = NULL;php->capacity = php->size = 0;
}void HeapDestory(Heap* php) {assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}void swap(int* a, int* b) {int tmp = *a;*a= *b;*b = tmp;
}
//小堆
void AdjustUp(HPDataType* a,int child) {assert(a);int parent = (child - 1) / 2;while (child > 0) {if (a[parent] > a[child]) {swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}else {break;}}
}void HeapPush(Heap* php, HPDataType x) {assert(php);if (php->size == php->capacity) {int newcapacity = 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)malloc(sizeof(HPDataType) * newcapacity);if (tmp == NULL) {perror("malloc fail!");}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;AdjustUp(php->a,php->size);php->size++;
}
//从给定的子节点开始,不断向上与其父节点进行比较和可能的交换,直到达到根节点或找到一个满足最大堆性质的父节点为止。
void AdjustDown(int* a, int n, int parent) {assert(a);int child = parent * 2 + 1;while (child < n) {if (child + 1 < n && a[child] < a[child + 1]) {child++;}if (a[parent] < a[child]) {swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else {break;}}
}void HeapPop(Heap* php) {assert(php);swap(&php->a[0], &php->a[php->size - 1]);AdjustDown(php->a, php->size,0);php->size--;
}HPDataType HeapTop(Heap* php) {assert(php);assert(php->size > 0);return php->a[0];
}int HeapSize(Heap* php) {assert(php);return php->size;
}int HeapEmpty(Heap* php) {assert(php);return php->size;
}test.c
#define _CRT_SECURE_NO_WARNINGS
#include "Heap.h"
int main() {Heap hp;HeapInit(&hp);HeapPush(&hp, 7);HeapPush(&hp, 6);HeapPush(&hp, 5);HeapPush(&hp, 4);HeapPush(&hp, 3);HeapPush(&hp, 2);HeapPush(&hp, 1);for (int i = 0; i < hp.size; i++) {printf("%d ", hp.a[i]);}HeapPop(&hp);printf("\n");for (int i = 0; i < hp.size; i++) {printf("%d ", hp.a[i]);}printf("\n");printf("堆顶元素为%d\n", HeapTop(&hp));if (HeapEmpty(&hp)) {printf("堆不为空\n");}else {printf("堆为空\n");}return 0;
}🍇堆排序
🌴深度剖析
第一步:建堆
(升序建大堆,降序建小堆)
以升序为例:
从最后一个父节点开始向前遍历,向上调整(大的上小的下)。
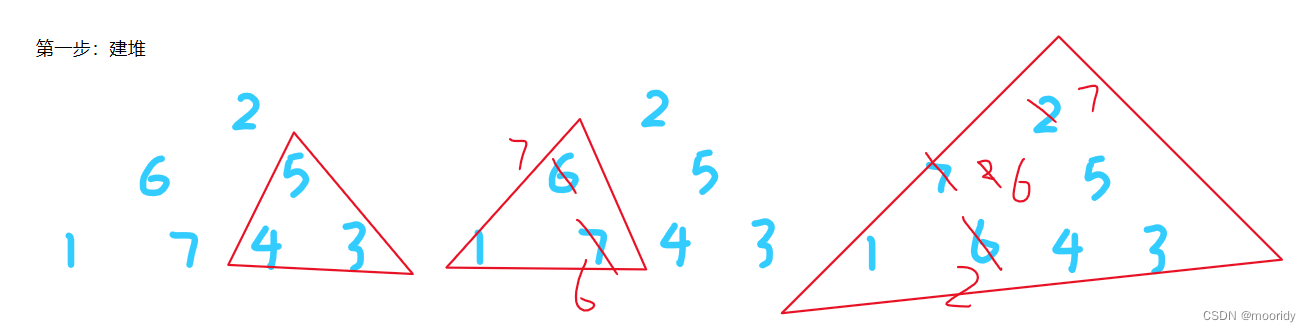
//建堆:从倒数第一个父节点开始向前遍历,向下调整for (int i = (n-1-1)/2; i >=0 ;i--) {AdjustDown(a,n,i);}第二步:排序
1.首尾元素交换(左图)
2.再向下调整(大的上小的下),这样调整后的堆顶元素必为调整范围内的最大值,经过下一轮的首尾元素交换后,就可以放入调整完的区域内。
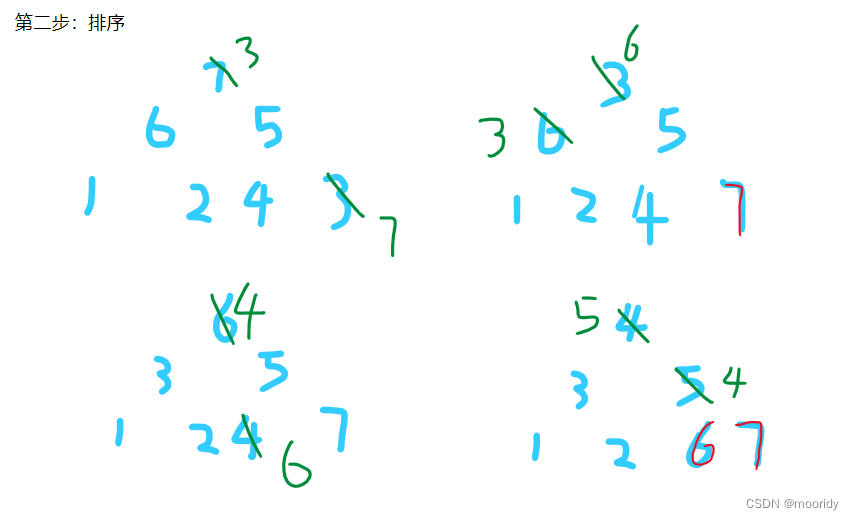

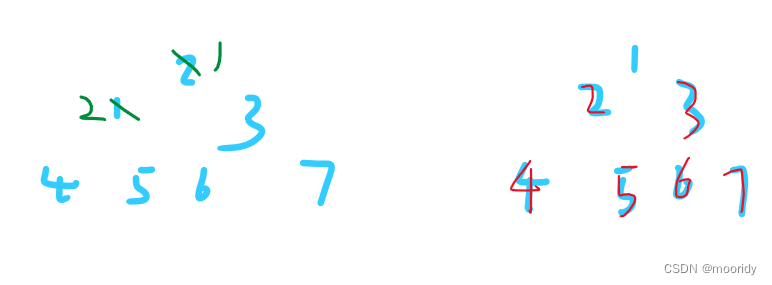
while (n - 1) {swap(&a[0], &a[n - 1]);AdjustDown(a, n-1,0);n--;🥳代码实现
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <assert.h>void swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}void AdjustUp(int* a, int child) {assert(a);int parent = (child - 1) / 2;while (child > 0) {if (a[parent] < a[child]) {swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}else {break;}}
}
void AdjustDown(int* a, int n, int parent) {assert(a);int child = parent * 2 + 1;while (child < n ) {if (child + 1 < n && a[child] < a[child + 1]) {child++;}if (a[parent] < a[child]) {swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else {break;}}
}//升序建大堆 降序建小堆
void HeapSort(int* a, int n) {//建堆:从倒数第一个父节点开始向前遍历,向下调整for (int i = (n-1-1)/2; i >=0 ;i--) {AdjustDown(a,n,i);}//先将首尾元素进行交换,再向下调整while (n - 1) {swap(&a[0], &a[n - 1]);AdjustDown(a, n-1,0);n--;}
}int main() {int a[7] = { 2,6,5,1,7,4,3 };int n = sizeof(a) / sizeof(a[0]);HeapSort(a, n);for (int i = 0; i < n; i++) {printf("%d ",a[i]);}return 0;
}🍉从时间复杂度角度分析建堆为何采取向下调整?
下面将分别分析向下调整算法建堆和向上调整算法建堆的区别:
向下调整建堆
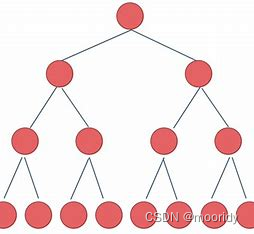
假设节点数量为N,树的高度为h
第一层,2^0个节点,需要向下调整h-1层
第二层,2^1个节点,需要向下调整h-2层
第三层,2^2个节点,需要向下调整h-3层
……
第h层,2^h个节点,需要向下调整0层
可以看出:节点少的层向下调整得多,节点多的层向下调整得少
计算向下调整建堆最坏情况下合计的调整次数:
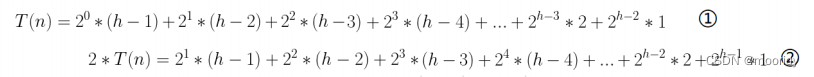
通过错位相减法可得:
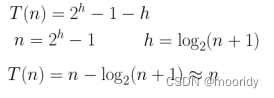
因此向下调整建堆的时间复杂度为O(N)
向上调整建堆:

假设节点数量为N,树的高度为h
第一层,2^0个节点,需要向下调整0层
第二层,2^1个节点,需要向下调整1层
第三层,2^2个节点,需要向下调整2层
……
第h层,2^h个节点,需要向下调整h-1层
可以看出:节点少的层向上调整得少,节点多的层向上调整得多。
T(h)=2^1*1+2^2*2+……+2^(h-2)*(h-2)+2^(h-1)*(h-1)
同样由错位相减法可得:
T(h)=-(2^2+2^3+……+2^(h-1))+2^h*(h-1)-2^1
整理可得:
T(N)=-N+(N+1)*(log2(N+1)-1)+1
因此向上调整建堆的时间复杂度为O(N*logN)
所以我们选择向下建堆算法明显效率更高。

