当前位置：首页 > news >正文

常见排序算法之选择排序

news 2025/7/8 22:03:20

一、选择排序

1.1 什么是选择排序？

1.2 思路

1.2.1 思路一

1.2.2 优化思路

1.3 C语言源码

1.3.1 思路一

1.3.2 优化思路

二、堆排序

2.1 调整算法

2.1.2 向上调整算法

2.1.3 向下调整算法

2.2 建堆排序

一、选择排序

1.1 什么是选择排序？

选择排序是一种简单直观的排序算法。它的基本思想是从未排序的数据中选择最小（或最大）的元素，放到已排序数据的末尾，同时将该元素从未排序部分删除，直到所有元素都排序完成。

具体操作为，首先找到未排序部分的最小元素，并与未排序部分的第一个元素交换位置，这样就完成了一次选择。然后，将接下来未排序部分的第一个元素视为最小，找到最小元素并与未排序部分的第一个元素交换位置，以此类推，直到所有元素都排序完成。

选择排序的时间复杂度为O(n^2)，是一种不稳定的排序算法。虽然它的效率相对较低，但由于其简单易实现，可以用于排序小规模的数据集合。然而对于大规模数据集合，选择排序通常不是一个最佳的选择。

1.2 思路

1.2.1 思路一

遍历第一趟数组，找出数组的最小值，与第一个数据交换
遍历第二趟数组，继续找出最小值，与第二个数据交换
重复上述动作

1.2.2 优化思路

一趟遍历找到最大和最小的元素，分别把他们放到数组的两端
缩小区间最大最小值包含的区间，找到次大，次小的元素
以此类推，直到头尾下标重合

该思路可能存在的问题：当maxi的位置与begin重合，则begin先与mini的位置交换，此时max位置的最大值被交换走，导致end与max交换的数值是错误的（图解见下）

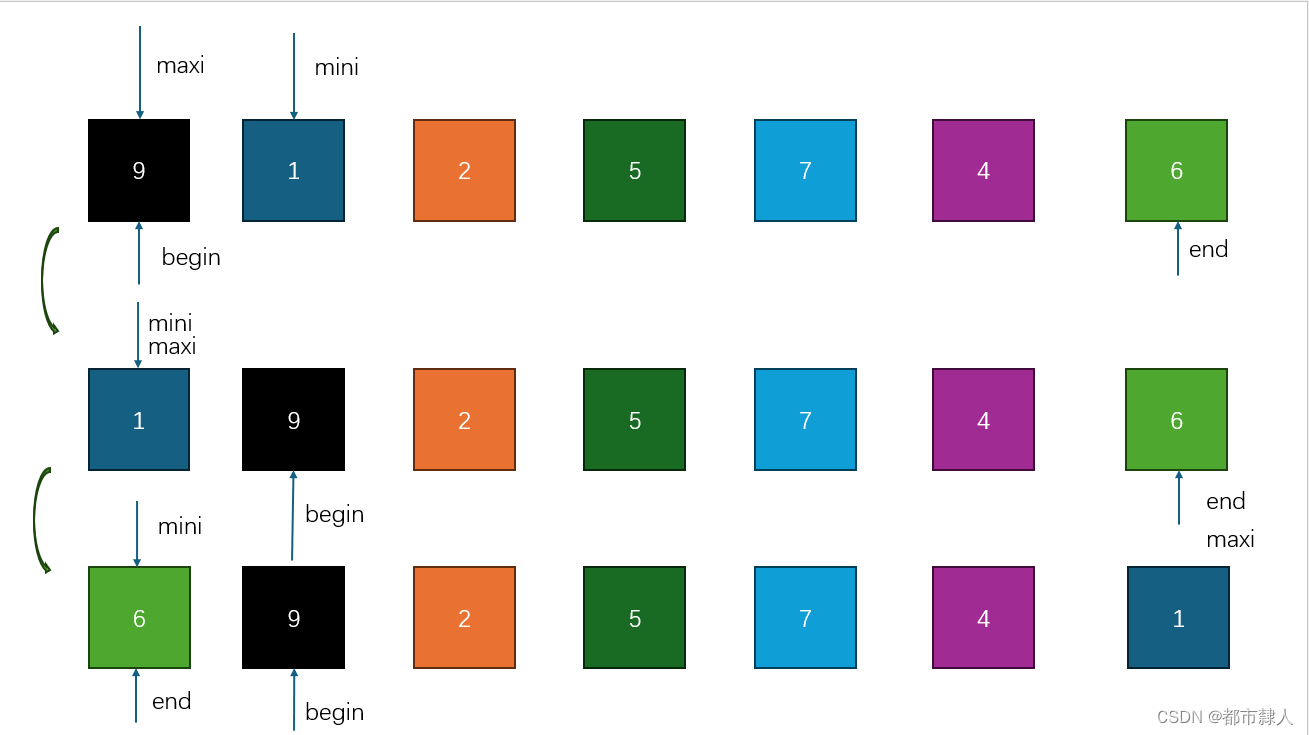
1.3 C语言源码

1.3.1 思路一

//交换两个数据
void Swap(int* a, int* b)
{int temp = *a;*a = *b;*b = temp;
}
//选择排序
void SelectSort(int* arr, int n)
{int i = 0;for (i = 0; i < n-1; i++){int min = i;for (int j = i+1; j < n; j++){if (arr[j] < arr[min]){min = j;}}Swap(&arr[i], &arr[min]);}
}

1.3.2 优化思路

//交换两个元素
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//插入排序
void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;while (begin < end){int mini = begin;int maxi = begin;//在区间中找出最小的数和最大的数for (int i = begin + 1; i <= end; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}//最小的数与首交换Swap(&a[begin], &a[mini]);//特殊情况修正if (begin == maxi)				{maxi = mini;}//最大的数与尾交换Swap(&a[end], &a[maxi]);begin++;end--;}
}

二、堆排序

2.1 调整算法

详细图解请见：二叉树的顺序实现-堆-CSDN博客

2.1.2 向上调整算法

void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}

2.1.3 向下调整算法

void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//找出小孩子if (child + 1 < n && a[child + 1] < a[child]){++child;}//交换if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}