ACWing蓝桥杯每日一题

一直没时间去总结算法，终于有空可以总结一下刷的acwing了，因为没时间所以最近只刷了ACWING的蓝桥杯每日一题。。。真是该死

1.截断数组

首先我们要知道，如果sum(a)不能被3整除或者len(a) < 3 ，那么他肯定没法让截断的三个子数组和都一样
然后我们只要把平均值算出来，从前往后遍历，我们会得到1average截断点，也会得到2average截断点，意思就是说在1average截断点前的子数组加和为average ，那么其实答案就是 2average截断点的个数 + 在2average截断点之前的 1average截断点的个数，，所以我们只要让当tot = 2average时，答案 += 当时的1average 截断点的个数就好了

注意！在判断tot = average 还是 2average 时，要先判断是否等于2average，因为当tot等于0时，1average == 2average，你如果先判断了2*average，就会把1级截断点和二级截断点在同一个地方。。

同时考虑到数组全为0的情况，那么这种情况我们就C（len-1,2）就行了

具体代码如下

n = int(input())
a = [int(x) for x in input().split()]
def c(a,b):res = 1while b:res = res * a / ba -= 1b -= 1return int(res)
if sum(a) % 3 != 0 or len(a) < 3:print(0)
elif a == [0]*len(a):print(c(len(a)-1,2))
else:average = sum(a) // 3one = 0res = 0tot = 0for i in range(n-1): # 最后一个点不能考虑进去，要留下一个做第三部分tot += a[i]if tot == 2*average: res += oneif tot == average:one += 1print(res)

2.改变数组元素

初始化一个V 数组，大小为（n+1）初始化都是0
只需要去通过i去遍历a[i],遍历到第i次时，我们就把 i - a[i] + 1 到 i 全部加1，
i就可以代表V数组实际的长度应该是多少，例如当i = 5 ，那么其实V数组实际上长度是5，因为末尾只被加了5个0 ，然后假设a[5] = 2 ，那就是V[4] 和 V[5] + 1 ，这里为什么可以+ 1 不用让他等于1？因为整个流程没有减过，所以只要这个位置不等于0，就代表他被改变过，一定等于1
然后这种从i - a[i] + 1 到 i 全部加1的实现通过差分就很好实现了

具体代码如下

def add(l,r):  # 差分,最后前缀和后L到R + 1V[l] += 1V[r+1] -= 1 t = int(input())
for _ in range(t):## 第i次就等于从i- a[i] + 1到i 全变为1## 利用差分，从 i - a[i] + 1 到 i 全部加1 ，因为不会减，所以最后只要前缀和不是0就代表他被换过n = int(input())a = [int(x) for x in input().split()]V = [0]*(n+1) #直接开一个这么大的数组,直接开N  TLE了for i in range(1,n+1):  # i要从1开始，i等于1表示数组中末尾添加了一个0if a[i-1] == 0:continueif (a[i-1] >= i):add(0,i-1)else:add(i - a[i-1],i-1)for i in range(n):V[i+1] += V[i]for i in range(n):if V[i] != 0 :print(1,end = ' ')else: print(0,end = ' ')print()

3.我在哪？

这题我觉得主要的就是需要考虑到字符串的哈希存储，因为字符串没法像数组那样去用下标来找到第几个字母，所以得先将字符串进行哈希存储，然后再遍历遍历列表，例如k = 4 ，就字符串前四个的值放入集合中，然后字符串2-5的哈希值看看在不在集合中，如果在，就返回False
然后要找K的话其实从1开始遍历就好了，只不过那样时间复杂度是O（n）很可能会被卡，最好用二分

具体代码如下

字符串哈希

## 核心思想：将字符串看成P进制数，P的经验值是131或13331，取这两个值的冲突概率低
##  小技巧：取模的数用2^64，溢出的结果就是取模的结果
## h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
N = 10**5 +10
P = 131
M = 91815541
h = [0] * N
p = [0] * N
p[0] = 1
n = int(input())
s = " " + input()
for i in range(1,n+1):h[i] = h[i-1]*P + ord(s[i]) % M
def get(l,r):return (h[r] - h[l-1] * P**(r-l+1)) % M
def check(k):a = set()for i in range(1,n - k + 2):if get(i,i + k -1) in a:return Falseelse:a.add(get(i,i+k-1))return Trueif __name__ == '__main__':l,r = 1,nwhile l < r:mid = (l + r) >> 1if check(mid): r = midelse: l = mid + 1print(r)

4.字符串删减

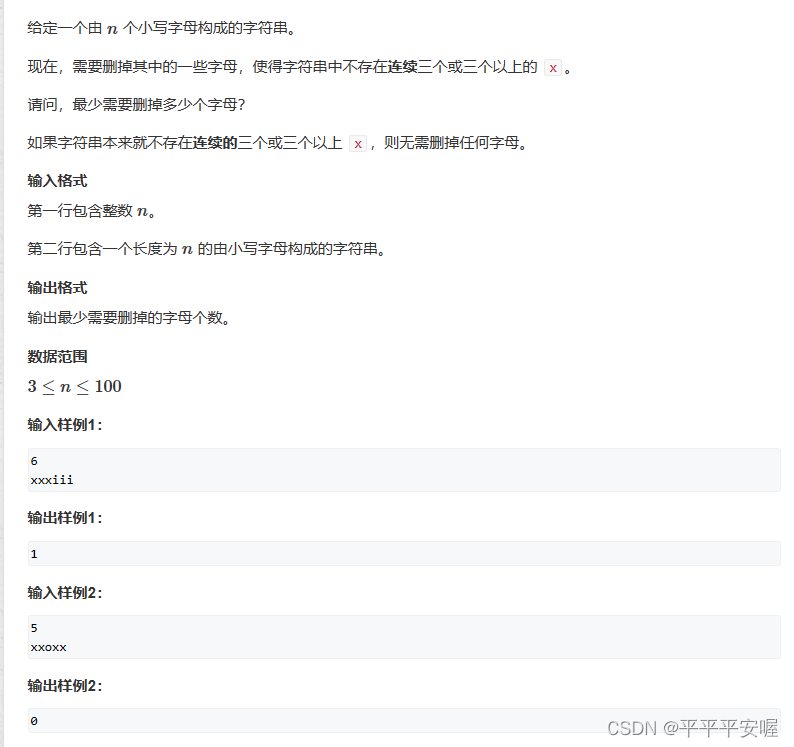
这个相对于Python来说就很好做吧，别的我不知道，就是记录一下连续x的长度，然后最后计算一下就好了，直接看代码吧

具体代码如下

n = int(input())
s = input()
lens = 0
lenshuzu = [] # 记录每一段连续的数组
for i in s:if i == 'x':lens += 1else:lenshuzu.append(lens)lens = 0
lenshuzu.append(lens)
res = 0
for i in lenshuzu:if i >= 3:res += i - 2
print(res)

5.砖块

这题我选择算是用贪心的方法去做吧，分为两种，全变黑和全变白
如果是全变白，那么就当看到黑的砖块，就把他变白就好了
后面的输入操作的我可能是写的有点麻烦了。。有大佬有更简便的可以指导一下

具体代码如下

T = int(input())
for _ in range(T):k = int(input())p = input()p2 = p #记录一下p = list(p)caozuo1 = []ans1 = 0flag1 = Falseflag2 = False# 全变白色for i in range(k-1):if p[i] == 'B':p[i] = 'W'if p[i+1] == 'B':p[i+1] = 'W'else: p[i+1] = 'B'caozuo1.append(i+1)ans1 += 1if p == ['W']*k :flag1 = True# 全变黑色p2 = list(p2)caozuo2 = []ans2 = 0for i in range(k-1):if p2[i] == 'W':p2[i] = 'B'if p2[i+1] == 'W':p2[i+1] = 'B'else: p2[i+1] = 'W'caozuo2.append(i+1)ans2 += 1if p2 == ['B']*k:flag2 = Trueif flag1 and flag2:if ans1 < ans2:print(ans1)if caozuo1:for i in caozuo1:print(i,end = ' ')print()continueelse:print(ans2)if caozuo2:for i in caozuo2:print(i,end = ' ')print()continueif flag1:print(ans1)if caozuo1:for i in caozuo1:print(i,end = ' ')print()continueif flag2:print(ans2)if caozuo2:for i in caozuo2:print(i,end = ' ')print()continueprint(-1)

6.树的遍历

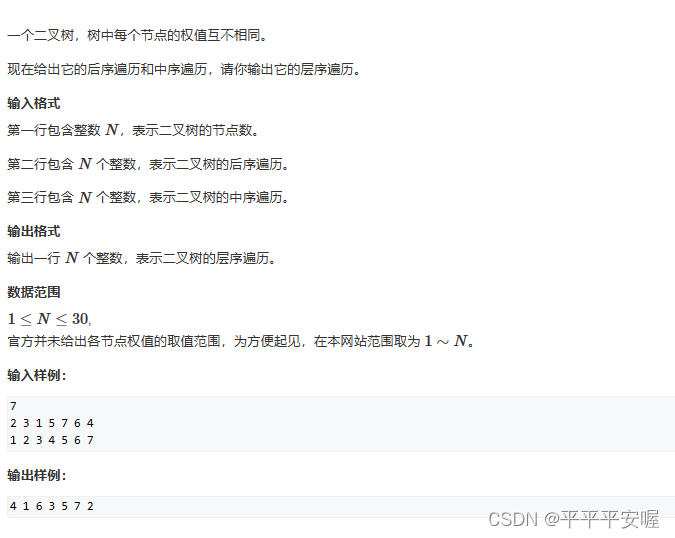
这题就递归做，可以通过中序和后序找到根节点的左右子树的中序和后序，然后递归往下建立

建立完一棵树之后就用Dfs去搜索就好了

具体代码如下

class TreeNode(object):def __init__(self,x):self.val = xself.left = Noneself.right = Noneclass Solution(object):def buildTree(self,inorder,postorder):  # inorder是中序，postorder是后序if not postorder:return Noneroot = TreeNode(postorder[-1])root_index = inorder.index(postorder[-1]) # 根节点在中序中的坐标left_i = inorder[:root_index] # 根据中序确定左右子树right_i = inorder[root_index + 1:]len_li = len(left_i)  # 左子树长度left_p = postorder[:len_li]  # 确定后序遍历的左右子树right_p = postorder[len_li:-1]root.left = self.buildTree(left_i,left_p)root.right = self.buildTree(right_i,right_p)return root
def bfs(root):  #广搜进行层序遍历if root == None:returnq = []q.append(root)head = 0while len(q)!=0:print(q[head].val,end=' ')if q[head].left != None:q.append(q[head].left)if q[head].right != None:q.append(q[head].right)q.pop(0)n = int(input())posto = [int(x) for x in input().split()]
inord = [int(x) for x in input().split()]solution = Solution()
root = solution.buildTree(inord,posto)
bfs(root)

7.亲戚

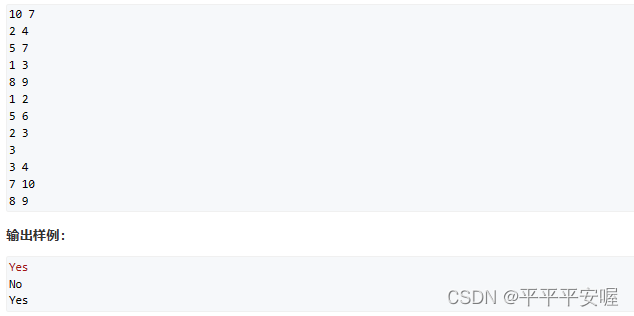
啊这题典型的并查集，让同样是亲戚的有同一个祖先就好了，不用管祖先是谁
简单说一下并查集吧
就是有一个p数组，代表自己的父亲是谁，然后就是每次遍历两个a,b，如果a和b没有同一个祖先，我们就让a的祖先 去 变成b的祖先的儿子，这样a和b就有同一个祖先了吧？
然后怎么找a和b的祖先呢，这也是并查集的精髓所在，一个find函数

def find(x):if p[x] != x:p[x] = find(p[x])return p[x]

如果x的父亲不是自己，就代表x不是这个家族的祖先对吧，那么让p[x]等于find(p[x])，find(p[x])就是找到p[x]的祖先，一层一层网上找，这个find函数的精髓在于，他会让p[x] = find(p[x]) 就是如果你现在他这个找到祖先的一条线的P[x]都会直接变为他们的祖先，而不是他们的父亲
然后就很好做了，看看他们的祖先是否一样就能代表是不是一个群体了

具体完整代码如下

import sys
# 不知道为什么用map(int,input().split())会被卡。。
N, M = map(int, sys.stdin.readline().strip().split())
p = [i for i in range(N + 1)]def find(x):if p[x] != x:p[x] = find(p[x])return p[x]for i in range(M):a, b = map(int, sys.stdin.readline().strip().split())pa, pb = find(a), find(b)if pa != pb:p[pa] = pb
q = int(input())
for i in range(q):a, b = map(int, sys.stdin.readline().strip().split())if find(a) == find(b):print('Yes')else:print('No')

8.笨拙的手指

这题我的想法是，把二进制的每一位都变一下，就是把可能的正确答案都存在一个列表中，然后去对比二进制和三进制的列表，找到相同的，二进制的好做，0和1之间变换只要用^就可以了，三进制就需要在遍历一下1-3 ，如果与当前位不同再去变，看代码吧，蛮容易看懂的，比我写清晰多了

具体代码如下

import copy
er = input()
three = input()
erjinzhi = []
sanjinzhi = []
for i in range(len(er)):erjinzhi.append(int(er[i]))
for j in range(len(three)):sanjinzhi.append(int(three[j]))
res_2 = []
res_3 = []
copy_erjinzhi = copy.deepcopy(erjinzhi)
for i in range(len(erjinzhi)):  #勉强算20erjinzhi = copy.deepcopy(copy_erjinzhi)erjinzhi[i] = erjinzhi[i] ^ 1lenlen = 2**(len(erjinzhi)-1)res = 0for j in erjinzhi:res += j*lenlenlenlen >>= 1res_2.append(res)copy_sanjinzhi = copy.deepcopy(sanjinzhi)
for i in range(len(sanjinzhi)):  #勉强算20for j in range(3):sanjinzhi = copy.deepcopy(copy_sanjinzhi)if sanjinzhi[i] != j:sanjinzhi[i] = jlenlen = 3**(len(sanjinzhi) - 1)res = 0for k in sanjinzhi:res += k*lenlenlenlen //= 3res_3.append(res)
res = 0
for i in res_2:for j in res_3:if i == j:res = max(res,i)
print(res)

9.裁剪序列

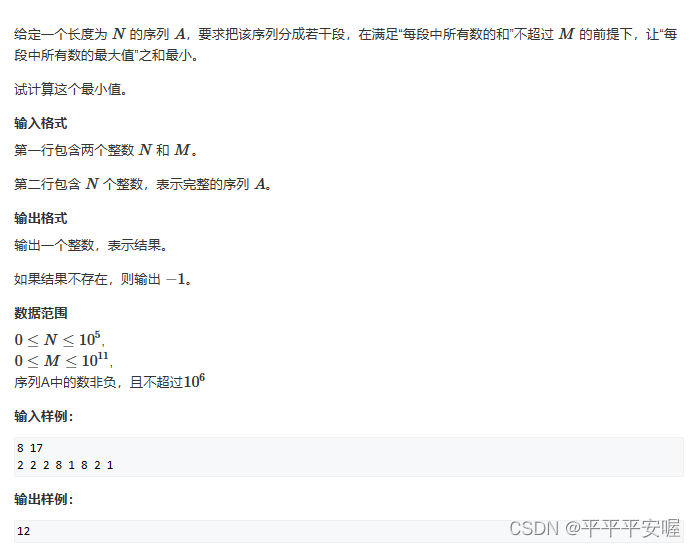
我也没搞懂。。抱歉

10.周期

首先，我们要知道KMP算法的next数组是什么用的，他是可以找到后缀和前缀相同的个数的一个数组，具体求法可以看我的KMP手写算法那一个

然后我们只需要从头到尾扫一遍，只要（i % (i-next[i])）== 0 就代表有重复节，并且长度是i // ( i - next[i])
例如 abcabcabcabc 当i等于12时，就是全长了嘛，然后next[i] = 9
满足条件吧？ 长度为4

具体代码如下

def find_next(p):next = [0] * (len(p)+1)j,k = 0,-1next[0] = -1  # 防止死循环 k一直等于0 j也不加while(j <= len(p) - 1):if (k == -1 or p[j] == p[k]):j += 1k += 1next[j] = kelse:k = next[k]next[0] = 0return nextif __name__ == '__main__':flag = 1while True:n = int(input())if n == 0: breakprint('Test case #{}'.format(flag))s = input()next = find_next(s)for i in range(2,n+1):if i % (i - next[i]) == 0 and next[i]:print('{} {}'.format(i,i//(i - next[i])))print()flag += 1

11.最大异或和

先求出前i个数的异或和sum[i]，再在大小为m的滑动窗口内进行trie.

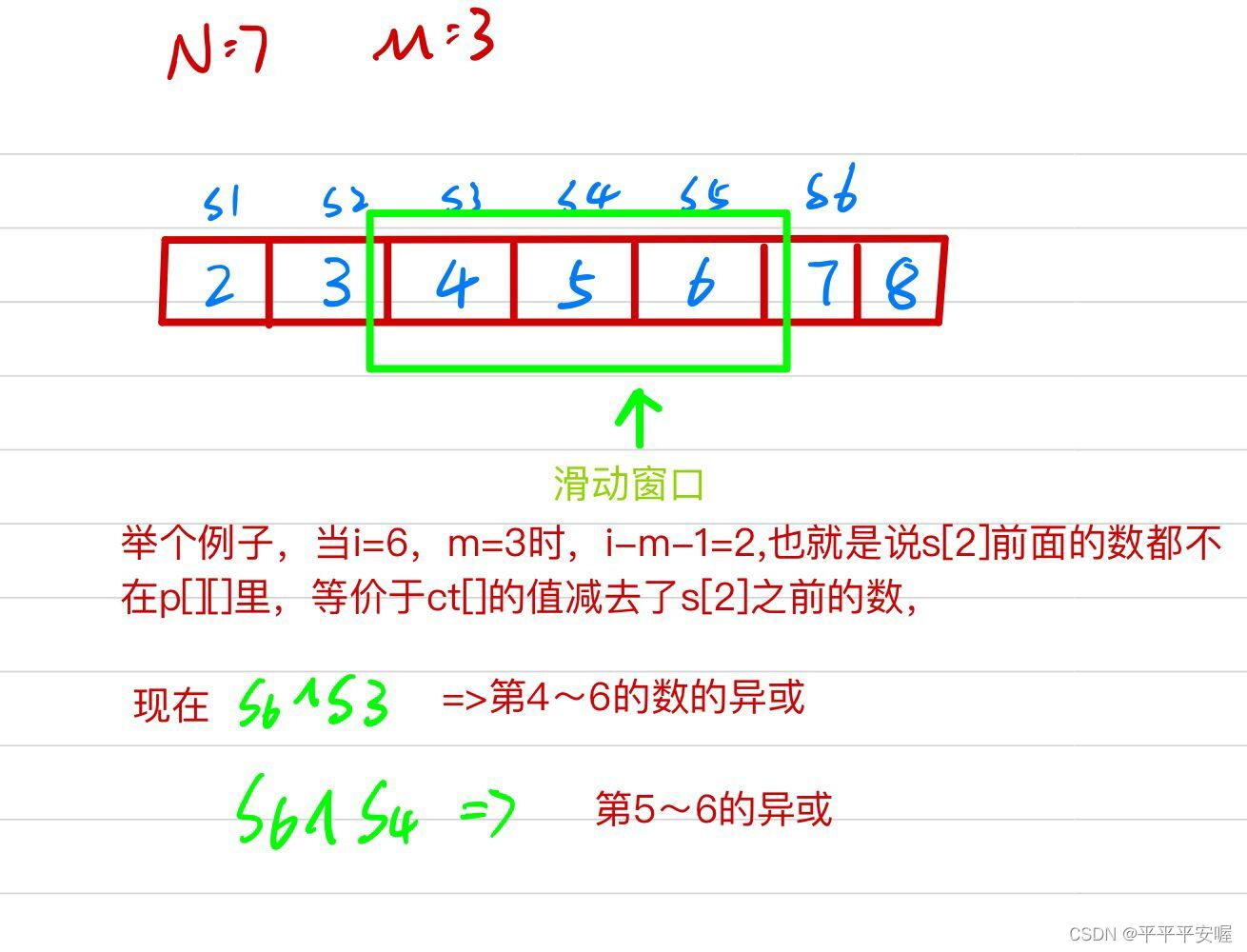
参考自https://www.acwing.com/solution/content/48648/
用trie树嘛，每个数都被记录在一个trie树中，一个二分数，每个节点都有一个0，1孩子，我们这边用了30层，完全够用了，然后把每个数的二进制数给存进去
先计算前缀异或和s[i]
要求异或和a[l]^…a[r] 转化为前缀异或和数组(s[r]^s[l-1])

具体代码如下

N = 100010 * 31
M = 100010
son = [[0]*2 for _ in range(N)]  #　son[p][n] n 只有两个取值为0和1，
idx = 0
s = [0]*M
cnt = [0]*N # cnt变量表示这个节点在构建字典树的时候保存了几次
# 遍历的时候，如果节点的cnt>0，就代表可以接着往下走，
def insert(x,v):global idx,son,s,cntp = 0for i in range(30,-1,-1):# 意思就是一棵树有30层，来代表每个数的二进制数u = x >> i & 1if(int(not son[p][u])):  # p的儿子有0和1两条路径idx += 1son[p][u] = idxp = son[p][u]            #p变为儿子，如果v是1，那么这条路径的p的1儿子+1cnt[p] += v              ### 我们遍历的话肯定是想从最高位开始，走1的分支，因为那样异或和才会更大
def query(x):# res 初始值为s[i]res = xp = 0for i in range(30,-1,-1):u = x >> i & 1       # x的二进制的第i位
## 现在x的第i位是u ，所以我们要走跟u相反的，这样他们异或才会为1if cnt[son[p][int(not u)]]:  # 就是存在和不存在 p 有两个儿子嘛，一个是0一个是1，如果u是1，就要看p的0的儿子还有没有u = int(not u)res ^= u << i  # u << i 因为之前 u = x >> i & 1 了，现在还回去# print(res)p = son[p][u]  # 接着往下走return resif __name__ == '__main__':n,m = map(int,input().split())a = [int(x) for x in input().split()]for i in range(1,n+1):s[i] = s[i-1]^a[i-1]insert(s[0],1)Res = 0for i in range(1,n+1):if i > m :insert(s[i - m - 1],-1)Res = max(Res,query(s[i]))insert(s[i],1)        # 把s[i]加入到树中print(Res)