当前位置：首页 > news >正文

C++数据结构之链表树图的存储

news 2025/8/18 0:58:02

本文主要介绍用数组存储，结构只做简单介绍

文章目录

前言

结构体实现

1、链表的存储

2、树的存储

3、图的存储

数组实现

1、链表实现

2、树和图的实现

总结

前言

在正常工程中，我们通常使用结构体或者类，来定义并使用如链表，树，图这样的数据结构，但在算法中由于过多的调用，是打计算量大时候，结构体定义通常会慢，所以本文主要介绍一下数组实现上述数据结构。

结构体实现

对于结构或者类实现，就不做过多介绍，相关知识，在C++语言基础，面向对象程序设计以及数据结构内容都有涉及。下述直接给出相关代码实现

1、链表的存储

struct Node {int data;Node* next;
};// 创建一个新节点
Node* createNode(int data) {Node* newNode = new Node();newNode->data = data;newNode->next = nullptr;return newNode;
}// 在链表尾部插入节点
void insertAtEnd(Node*& head, int data) {Node* newNode = createNode(data);if (head == nullptr) {head = newNode;return;}Node* temp = head;while (temp->next != nullptr) {temp = temp->next;}temp->next = newNode;
}

2、树的存储

struct TreeNode {int data;TreeNode* left;TreeNode* right;
};// 创建一个新节点
TreeNode* createNode(int data) {TreeNode* newNode = new TreeNode();newNode->data = data;newNode->left = nullptr;newNode->right = nullptr;return newNode;   
}// 二叉树的前序遍历（根-左-右）
void preorderTraversal(TreeNode* root) {if (root == nullptr)return;cout << root->data << " ";preorderTraversal(root->left);preorderTraversal(root->right);
}

3、图的存储

class Graph {
private:int numVertices; // 图中顶点的数量list<int>* adjLists; // 邻接表public:Graph(int vertices) { // 构造函数，初始化图numVertices = vertices;adjLists = new list<int>[vertices];}void addEdge(int src, int dest) { // 添加边adjLists[src].push_back(dest); // 无向图需同时添加反向边adjLists[dest].push_back(src);}void printGraph() { // 打印图的邻接表表示for (int i = 0; i < numVertices; ++i) {cout << "顶点 " << i << " 的邻居节点：";for (const auto& neighbor : adjLists[i]) {cout << neighbor << " ";}cout << endl;}}
};

数组实现

1、链表实现

int head, e[N], ne[N], idx;
// head 表示头结点的下标
// e[i] 表示节点i的值
// ne[i] 表示节点i的next指针是多少
// idx 存储当前已经用到了哪个点// 初始化
void init()
{head = -1;idx = 0;
}
// 在链表头插入一个数a
void insert(int a)
{e[idx] = a, ne[idx] = head, head = idx ++ ;
}
//先用e存在a的值，ne存下指向的地址，head记录idx地址，idx指向下一个存储地址//为什么head=-1,这样最后可以判断到-1截止
//刚开始idx指向0，读入一个，指向下一个
for (int i = head; i != -1; i = ne[i]) cout << e[i] << ' ';遍历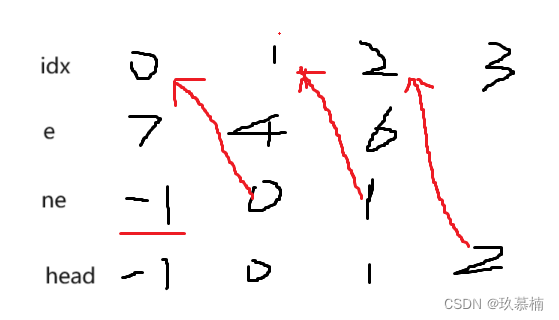

具体遍历实现如上，从head开始访问，然后不停通过ne得到地址，直到等于-1为止

当让理解如何存储是一样的，首先要存储读入a的值，即存入e中，同时使ne指向head指向的地址，head指向，idx指向地址，idx指向下一地址。具体实现上就是单链表的头插法。

2、树和图的实现

const int N = 100;  // 最大顶点数
const int M = 200;  // 最大边数int head[N];  
int e[M], ne[M];
int idx;      // 当前已经用到了哪个点// 初始化
void init() {memset(head, -1, sizeof(head));idx = 0;
}// 添加一条从u到v的有向边
void insert(int u, int v) {e[idx] = v;ne[idx] = head[u];head[u] = idx++;
}

首先边M = 2 * N保证数组不会溢出，其次需要head数组来存多个头结点，同时都需要初始化为-1

其实这个定义的就是邻接表，用邻接表的方式实现了一个有向图的存储，其中每个顶点的链表表示与其相连的边。如果给定的边是一棵无环有向树（也就是树），则可以使用该数据结构进行存储和操作。

所以上述代码对于树和图的通用，具体原理其实和单链表一样的，每一个都是单链表

无向图只需要俩条有向图就能实现