5月7日监控二叉树+斐波那契数
968.监控二叉树
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
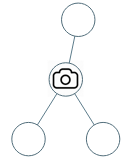
输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
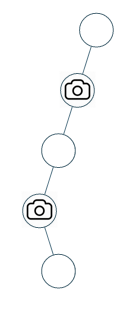
输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
思路
想半天想不出来然后去看了各路大神的题解,对比之下发现官方题解的说法完全是在冒充人类。
首先我们先要确定从二叉树的下面往上看,为什么不自顶向下呢?因为头节点放不放摄像头也就省下一个摄像头,但是叶子节点放不放摄像头省下的是指数级的摄像头。
那么从下往上看我们首先想到的是二叉树的后序遍历法(左-右-中),所以本题我们使用递归法来解。
并且,如果要达成局部最优的话,我们一定是在叶子节点的父节点安装摄像头,让所用摄像头最少,达成全局最优。
所以,大体思路就是从低向上遍历二叉树,先给叶子节点父节点放摄像头,然后隔两个节点放一个摄像头,直到到根节点。
但是怎样隔两个节点放一个摄像头呢?此时我们就需要状态转移的公式来记录每个节点的状态。每个节点可能有三种状态:
0:该节点无覆盖
1:该节点有摄像头
2:该节点有覆盖
空节点一律视为有覆盖的情况,因为若把空节点视为无覆盖,那么空节点的父节点——叶子节点就必须放置一个摄像头,这与本意冲突;若把空节点视为有摄像头,那么叶子节点就为有覆盖,那么隔两个节点才会放一个摄像头,实际上没有监控到叶子节点,所以空节点只能视为有覆盖。
那么,对于每个节点的处理逻辑我们可以分为四类情况:
1、左右节点都有覆盖:该节点一定无覆盖
2、左右节点至少有一个无覆盖:该节点一定放摄像头
3、左右节点至少有一个摄像头:该节点一定有覆盖
4、头节点无覆盖:头节点再加一个摄像头。
代码
class Solution {int res=0;public int minCameraCover(TreeNode root) {return dfs(root)==0?res+1:res;}private int dfs(TreeNode node){if(node==null){return 2;}int left=dfs(node.left);int right=dfs(node.right);if(left==0||right==0){res++;return 1;}if(left==1||right==1){return 2;}return 0;}}灵茶山艾府的思路我没理解,二刷的时候再研究。
509.斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
思路
经典递归解法:
class Solution {public int fib(int n) {if(n==1){return 1;}else if(n==0){return 0;}else {return fib(n-1)+fib(n-2);}}}dp解法:
确定dp数组含义
dp[i]的定义为:第i个数的斐波那契数值为dp[i]
递推公式:dp[i] = dp[i - 1] + dp[i - 2];
初始化:dp[0]=0,dp[1]=1
代码
class Solution {public int fib(int n) {if (n <= 1) return n; int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 1;for (int index = 2; index <= n; index++){dp[index] = dp[index - 1] + dp[index - 2];}return dp[n];}
}空间复杂度可以进一步优化,因为不用维护整个dp数组:
class Solution {public int fib(int n) {if (n < 2) return n;int a = 0, b = 1, c = 0;for (int i = 1; i < n; i++) {c = a + b;a = b;b = c;}return c;}
}